P3916 图的遍历

原题

题目描述

给出N个点，M条边的有向图，对于每个点v，求A(v)表示从点v出发，能到达的编号最大的点。

输入输出格式

输入格式：

第1 行，2 个整数N,M。

接下来M行，每行2个整数Ui​,Vi​，表示边(Ui​,Vi​)。点用1,2,⋯,N编号。

输出格式：

N 个整数A(1),A(2),⋯,A(N)。

输入输出样例

输入样例#1：

4 3
1 2
2 4
4 3

输出样例#1：

4 4 3 4

说明

• 对于60% 的数据，1≤N.K≤10^3；

• 对于100% 的数据，1≤N,M≤10^5。

分析

首先，你得注意到这个：1≤N,M≤10^5

由于数据范围太大用邻接矩阵存不下，所以我们采用邻接表储存

刚开始写的时候一下就想到了dfs，本人写了1个小时才发现会超时，那么这道题该用什么方法呢？

当你仔细思考这道题的时候你就会发现：你在从每个点出发去找它能到达的编号最大的点时，每搜到一个点你不能保证它是答案，而那些不是答案的点就浪费了你的宝贵时间

那么，如何避免这个问题呢？

很简单

你可以“倒着”搜：找哪些点能到i，而不是挨个找每个点能到达的编号最大的点

for example：

先从最大的点（9号点）开始，沿着能到达它的边反向搜索，搜索到的点能到达的编号最大的点就是它（“9”）

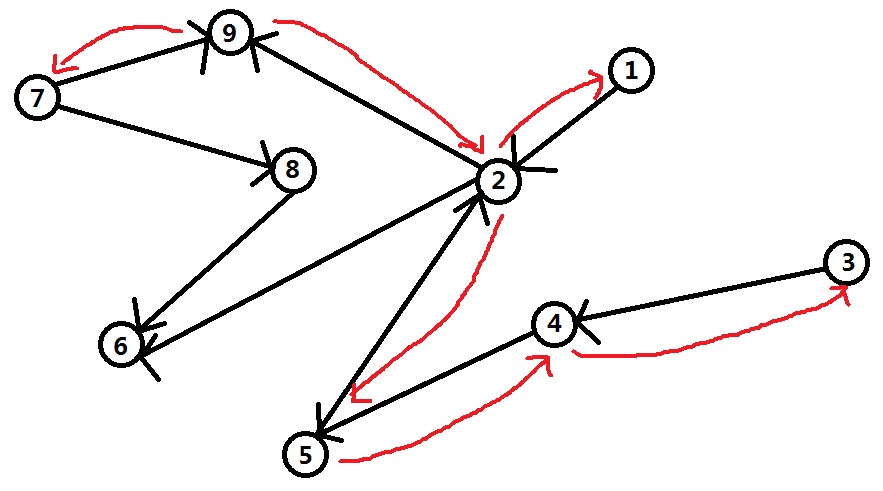
再从第二大的点（8号点）开始，沿着能到达它的边反向搜索，搜索到的点能到达的编号最大的点就是它（“8”）

再从第三大的点（7号点）开始，沿着能到达它的边反向搜索，但是7号点的入度（入度：指向这个点的边的数量叫这个点的入度）为0

再从第四大的点（6号点）开始，沿着能到达它的边反向搜索，搜索到的点能到达的编号最大的点就是它（“6”）

………………（以此类推，直到全图的每一个点都搜索过一遍）

注意：被搜索过的点以后就不需要搜索了

代码

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
int n,m;
int head[100001],nxt[100001],v[100001],cnt;
int ans[100001];
inline void add(int x,int y)
{
	cnt++;
	v[cnt]=y;
	nxt[cnt]=head[x];
	head[x]=cnt;
}
inline int dfs(int x,int num)
{
	ans[x]=num;
	for(int i=head[x];i;i=nxt[i])
	    if(ans[v[i]]==-1) dfs(v[i],num);
	return ans[x];
}
int main()
{
	memset(ans,-1,sizeof(ans));
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int x,y;
		cin>>x>>y;
		add(y,x);
	}
	for(int i=n;i>=1;i--)
	{
		if(ans[i]!=-1) dfs(i,ans[i]);
		else dfs(i,i);
	}
	for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
	return 0;
}