数据结构之堆(Heap):插入、取值、排序。
堆是一种数据结构,分为最小堆和最大堆,可以用二叉树来表示。
在二叉树的任意的一个三角结构中(一个父节点,两个子节点),需要满足以下两个条件:
1、父节点要是最小的,就是最小堆(或最大的,就是最大堆),两个子节点之间没有要求
2、数据插入的顺序是一层一层的,只有上一层存满,才会有下一层
下面我们以图片的形式演示最小堆的插入、取值、和排序操作,只要知道最小堆的原理,那么最大堆也就明白了。
假设我们有一个原始的最小堆如下:

插入操作:
当插入一个新值时,首先将值放到树的最后的位置,如下图所示。
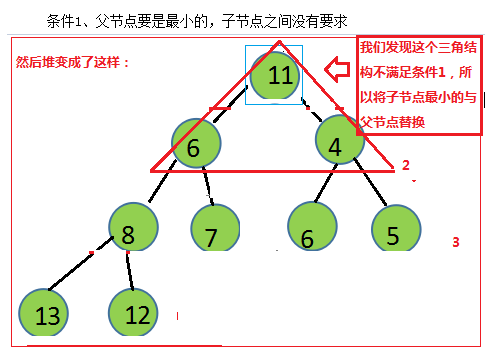
然后将这个值与父元素比较,如果不满足规则1,则与父元素替换(如下图所示)。
第一步
第二步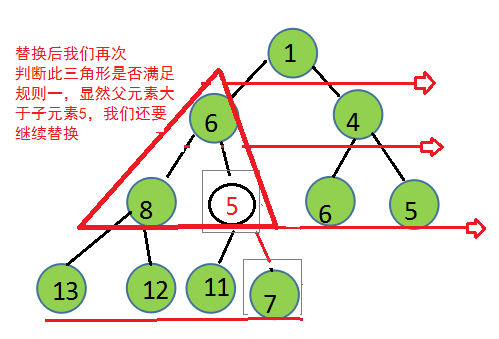
第三步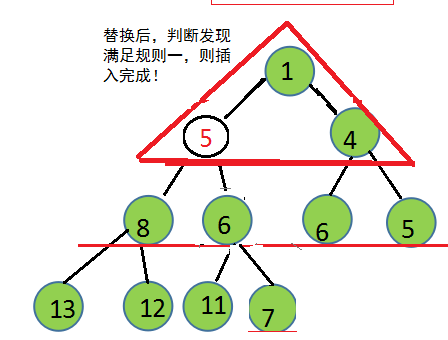
由图可知,在插入操作中,交换次数最大即为树的高度(log n)
取最小值操作:
在最小堆中,拿出一个最小值,当然就是拿出第一个数啦~不过拿完以后树不就没有“头”了?
不用担心,我们可以把最后一个数放到头的位置,这样树的结构就不会改变,而且操作简单(因为是最后一个数)。
当然,因为是最后一个数,必然会出现不满足条件1的情况,所以我们需要把新的树头与子元素比较替换,下面是图片演示:
假设我们有一个原始的最小堆如下所示,接下来我们要取最小值:
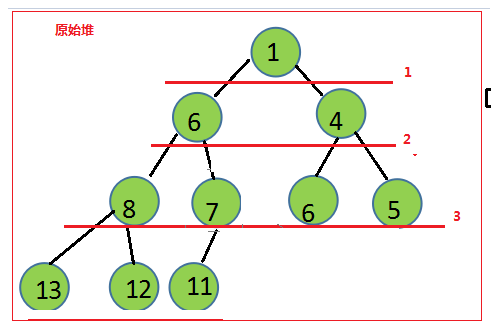
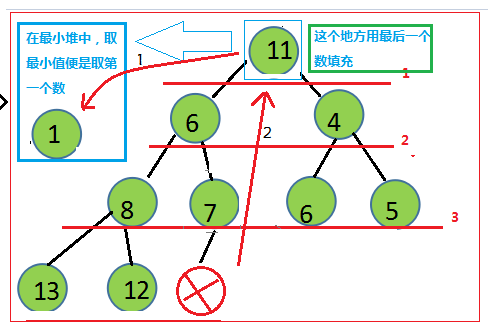
不过交换完很可能是不满足条件1的,那么我们就需要比较替换,替换规则是和两个子元素中最小的一个替换

由图可知,在取值操作中,交换次数最大也为树的高度(log n)
堆的排序:
我们知道了如何取最小值,那么堆的排序简单啦~只要依次取堆的最小值,那么当堆取完时,我们取出的数据不就是一个从小到大的序列嘛!