一、什么是回归(Regression)

一说回归最先想到的是终结者那句:I'll be back
regress,re表示back,gress等于go,数值go back to mean value,也就是I'll be back 的意思
在数理统计中,回归是确定多种变量相互依赖的定量关系的方法
通俗理解:越来越接近期望值的过程,回归于事物的本质
二、什么是线性回归(Linear Regression)
线性回归假设输出变量是若干输出变量的线性组合,并根据这一关系求解线性组合中的最优系数。
通俗理解:输出一个线性函数,例如(y=f(x))
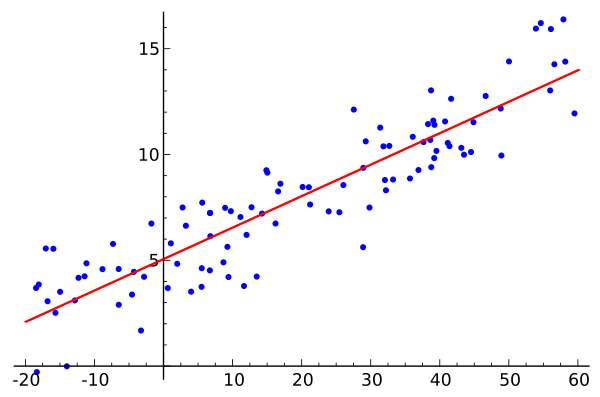
假定一个实例可以用列向量(x=(x_1;x_2;⋯,x_n))表示,每个(x_i)代表实例在第i个属性上的取值,线性回归就是都求出一组参数(wi,i=0,1,⋯,n),使预测输出可以表示为以这组参数为权重的实例属性的线性组合。
例如引入常量(x_i=1),线性回归试图学习的模型就是(f(x)=w^Tx=sum_{i=0}^nw_ix_i)
- 当实例只有一个属性时,输入输出之间关系就是二维平面的一条直线
- 当实例属性数目较多时,得到的是n+1维空间的一个超平面,对应一个维度等于于n的线性子空间
三、什么是单变量线性回归(Unary Linear Regression)
也叫一元线性回归,一元线性回归是分析只有一个自变量。
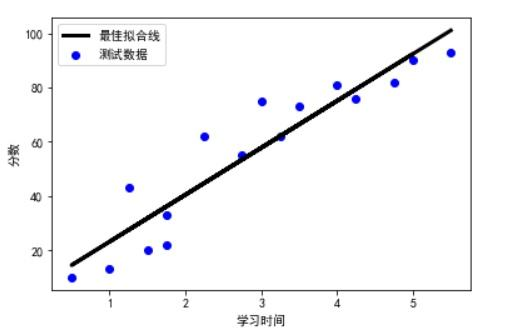
从一个输入值预测一个输出值,输入/输出的对应关系就是一个线性函数。
例如,肌肉块头和训练重量的关系可以简单看成一组线性的关系
四、什么是多元线性回归(Multiple Linear Regression)
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。
当样本的描述涉及多个属性时,这类问题就被称为多元线性回归。

例如,肌肉是睡眠、饮食、训练多种因素共同作用的结果。
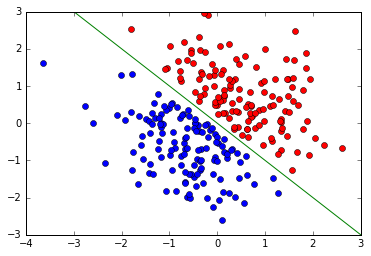
五、什么是逻辑回归(Logistic Regression)
线性回归能对连续值进行预测,而现实中学常见的另一类问题是分类,逻辑回归解决的就是分类问题
逻辑回归输出的实例属于每个类别的似然概率,似然概率最大的类别就是分类结果。
通俗理解:逻辑就是True或False,判断出是True还是False,相当于分类了
在二分类任务中,逻辑回归可以视为在平面直角坐标系上划定一条数据分类的判定边界。
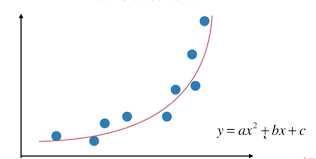
六、什么是多项式回归(Polynomial Regression)
研究一个因变量与一个或多个自变量间多项式的回归分析方法,称为多项式回归。
最终输出的是一个多项式回归方程,例如(y=ax+bx^2+c)
七、常见概念
欧几里得距离
指在m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到到原点的距离)
度量欧几里得空间中两点的距离。

均方误差
预测输出和真实输出之间的欧几里得距离
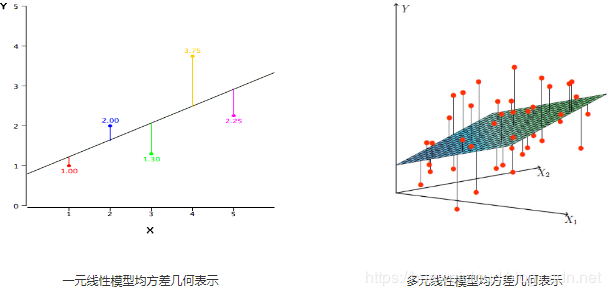
最小二乘法
使均方误差最小为目标的模型求解方法。
在单变量线性回归任务中,最小二乘法就是找到一条直线,使得样本到直线的欧几里得距离之和最小。

与梯度下降法的区别
最小二乘定义了最优化的目标函数,梯度下降要找到最优化问题的最优解,两者大致是目的和手段的关系。最小二乘是有解析解的,如果解析解难以求解,就可以用梯度下降这些数值方法
偏导数
固定面上一点的切线斜率。
导数和偏导数没有本质区别。
一元函数中,一个y对应一个x,导数只有一个。
一个z对应一个x和一个y,那就有两个导数了,一个是z对x的导数,一个是z对y的导数,称之为偏导。
