As you know, an undirected connected graph with n nodes and n - 1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value ai associated with it.
We call a set S of tree nodes valid if following conditions are satisfied:
- S is non-empty.
- S is connected. In other words, if nodes u and v are in S, then all nodes lying on the simple path between u and v should also be presented in S.
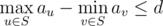 .
.
Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo 1000000007(109 + 7).
The first line contains two space-separated integers d (0 ≤ d ≤ 2000) and n (1 ≤ n ≤ 2000).
The second line contains n space-separated positive integers a1, a2, ..., an(1 ≤ ai ≤ 2000).
Then the next n - 1 line each contain pair of integers u and v (1 ≤ u, v ≤ n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.
Print the number of valid sets modulo 1000000007.
本来不想写博客的,但是最近做题目感觉自己水平好低啊,做题目的时候还是记录下一些自己得到的经验,方便总结。
题目大意
给你一棵带权树,让你计算一下有多少棵这样的树,这棵树中权值最大与最小的差小于d。
任何人一看就知道是树形dp,可是怎么dp啊? 一开始的想法是dp[u][m]表示u在这棵树中,而且这棵树最大节点的权值为m,这样来做一个二维的树形dp,感觉没有什么错误,可是发现好难实现啊,而且有好多细节没有办法处理。
最后还是看了题解,知道标准的dp为 dp[u]表示以u为根节点,最小(大)值为a[u]的树的数目,这样方程就好写了,可是我就是这样写了,发现为什么我算得值总是大于等于答案呢!好纠结,想不明白,再看看题解,上面说了,让我们注意重复的情况,我的天了,dp[u]中对于u肯定没有想同的啊,所以就不会有相同的情况,可是a[u]有可能相同啊,那怎么处理相同的时候呢,我们只要做的时候加一个判断,当他们的值相同时我们只考虑节点大(小)的就可以了,这样就避免的重复的情况,基本上这个题就OK了。