前言
二分图匹配的问题应该是比较常见的吧,用匈牙利算法就可以在(O(nm))的时间复杂度内解决这类问题。
二分图匹配
让我们从第一个问题开始讲起:什么是二分图?
用通俗的说法,如果一张图的点集能够被分为两个部分,且没有一条边连接的两个点在同一部分,那么这就是一张二分图。
那么什么是二分图匹配呢?
如果一个边集中的任意两条边都不连向同一个节点,也就是说每个节点只连一条边,那么这个边集就是一个匹配。
既然这样,那么二分图匹配就是二分图上的匹配了。
如何求解二分图最大匹配数:匈牙利算法
接下来我们要思考的问题是:如何求解二分图最大匹配数?
先来看一道模板题:【洛谷3386】【模板】二分图匹配。
想要求解这样的问题,我们就需要引入一个新的算法:由匈牙利数学家(Edmonds)发明的匈牙利算法(这也是它名字的由来)。
匈牙利算法的核心思想就是让位。
而且,它的让位,通常都是由已匹配好的点给未匹配的点让位。
一起来看一张图:
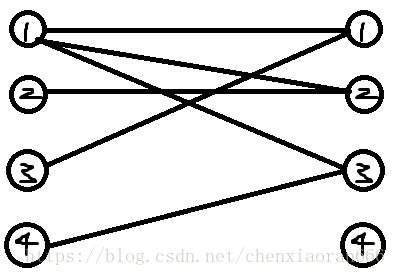
很显然,这是一张二分图。
那么这张图应该怎么用匈牙利算法来求解最大匹配数呢?我们可以一起来模拟一下匈牙利算法的求解过程。
首先,我们找到第一个右边第一个能与左边编号为1的节点匹配的节点,于是我们就找到了右边编号为1的节点:
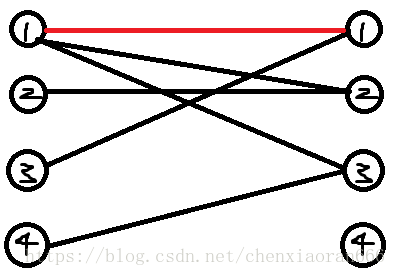
同理,我们为左边的2号节点找到了右边的2号节点:
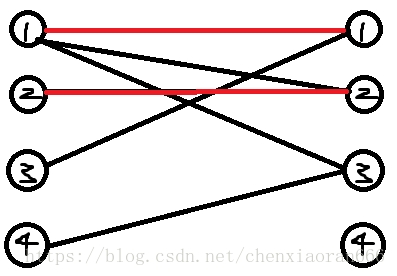
接下来轮到左边的3号节点了,但是,我们会发现第一个能与左边3号节点匹配的右边1号节点已经被匹配了。
怎么办呢?
这时,我们就要让与右边1号节点匹配的左边1号节点给3号节点让个位子出来。
于是,左边1号节点去找下一个能与左边1号节点匹配的节点,于是就找到了右边的2号节点(注意:左边1号节点并没有直接找到右边3号节点,即使3号节点是没有被匹配的)。
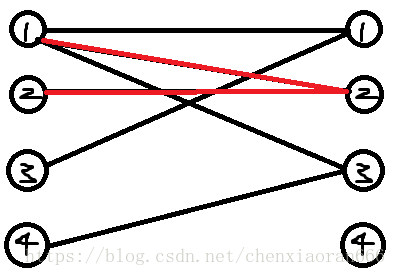
可是,右边2号节点也已经被匹配了。
这时我们就需要让与右边2号节点匹配的左边2号节点给1号节点让个位子出来。但是左边2号节点已经找不到能够与它匹配的节点了,所以我们要让1号节点再去找一个能与它匹配的节点。
然后,1号节点找到了右边3号节点,而右边3号节点恰好是没有被匹配的,于是,在左边3号节点匹配完之后,就变成了这样:
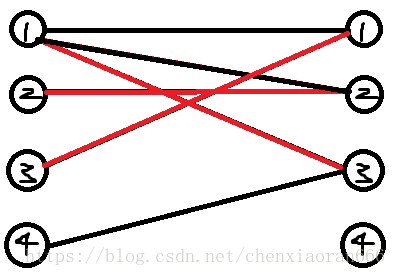
然后轮到左边4号节点了。
我们又需要让左边1号节点给4号节点让位了。
但是1号节点实在让不出位了,因此左边4号节点就找不到能够与它匹配的节点了。
综上所述,这张图的最大匹配数为3。
代码
讲了这么多,最后,我们再借助刚刚提到的那到模板题,我们一起来看一下匈牙利算法的具体实现吧:
#include<bits/stdc++.h>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
#define LL long long
#define swap(x,y) (x^=y,y^=x,x^=y)
#define tc() (A==B&&(B=(A=ff)+fread(ff,1,100000,stdin),A==B)?EOF:*A++)
#define pc(ch) (pp_<100000?pp[pp_++]=(ch):(fwrite(pp,1,100000,stdout),pp[(pp_=0)++]=(ch)))
#define N 1000
#define add(x,y) (e[++ee].nxt=lnk[x],e[lnk[x]=ee].to=y)
char ff[100000],*A=ff,*B=ff;
using namespace std;
int n,m,ee=0,lnk[N+5],vis[N+5],s[N+5];
struct edge
{
int to,nxt;
}e[N*N+5];
inline void read(int &x)
{
x=0;static char ch;
while(!isdigit(ch=tc()));
while(x=(x<<3)+(x<<1)+ch-48,isdigit(ch=tc()));
}
inline void write(int x)
{
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline bool GetPoint(int x,int t)//为节点x找到一个与其匹配的节点,t表示当前正在匹配的节点(记录t是因为这样就不用清空vis[]数组),返回值表示节点x能否找到一个与其匹配的节点
{
register int i;
for(i=lnk[x];i;i=e[i].nxt)//枚举与当前节点相邻的每一个节点
{
if(!(vis[e[i].to]^t)) continue;//如果一个节点已经在匹配编号为t的节点时访问过了,就跳过
vis[e[i].to]=t;//标记该节点已经在匹配编号为t的节点时访问过了
if(!s[e[i].to]||GetPoint(s[e[i].to],t))//如果这个节点没有节点与其匹配,或者与这个节点匹配的节点还可以找到一个新的节点与其匹配
{
s[e[i].to]=x;//将与这个节点匹配的节点记录为x
return true;//找到一个与x匹配的节点,返回true
}
}
return false;//找不到与x匹配的节点,返回false
}
int main()
{
register int i,x,y,edge_num,ans=0;
for(read(n),read(m),read(edge_num),i=1;i<=edge_num;++i)
{
read(x),read(y);
if(y<=m) add(x,y);
}
for(i=1;i<=n;++i) if(GetPoint(i,i)) ++ans;//如果这个节点能够找到一个与其匹配的节点,就将ans加1
return write(ans),0;
}