- 有一张(n)个点的简单无向图,给定每对点之间的简单路径条数(p_{i,j})。
- 求构造一张可能的图,或判断无解。
- (nle10^3,forall ple3)
对于(p=1)的情况
如果我们用并查集合并每一对(p_{i,j}=1)的(i,j),显然如果并查集中一个连通块里存在两点之间(p ot=1),就必然无解。
考虑(p=1)意味着两点之间只有一条简单路径,故发现只要对每个连通块随便构造出一棵树,然后就可以把这整个块缩成一个点。
于是(p=1)的情况就不复存在了。
对于(p=2)的情况
同样,我们用并查集合并每一对(p_{i,j}=2)的(i,j),显然如果并查集中一个连通块里存在两点之间(p ot=2)。就必然无解。
然后我们考虑每一个连通块,发现只要给这个连通块随便建一个环就可以了。
特别注意,如果一个连通块只有两个点,此时该连通块是无法构成环的。
对于(p=3)的情况
其实,只要存在(p=3),就必然无解。
如果存在(p_{A,B}=3),则下图是最简单的一种情况:
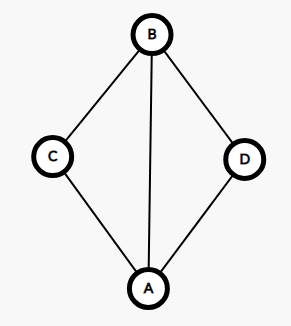
而此时,从(C)到(D)存在(4)条路径((CAD,CBD,CABD,CBAD)),超出了题目中给定的限制。
因此,(p=3)的情况不存在。
于是这道题就做完了。
代码:(O(n^2))
#include "supertrees.h"
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 1000
#define Array vector<vector<int> >
using namespace std;
int n,w[N+5],k[N+5],c[N+5],f[N+5];I int fa(CI x) {return f[x]^x?f[x]=fa(f[x]):x;}//并查集
Array b;int construct(Array p)
{
RI i,j,x,y;for(n=p[0].size(),b.resize(n),i=0;i^n;++i) f[i]=i,b[i].resize(n);//初始化
for(i=0;i^n;++i) for(j=0;j^n;++j) if(p[i][j]==3) return 0;//如果存在3,必然无解
for(i=0;i^n;++i) for(j=0;j^n;++j) p[i][j]==1&&(x=fa(i))^(y=fa(j))&&(f[x]=y,b[x][y]=b[y][x]=1);//把1在并查集上合并
for(i=0;i^n;++i) for(j=0;j^n;++j) if(i^j&&p[i][j]^1&&fa(i)==fa(j)) return 0;//判断是否存在矛盾
for(i=0;i^n;++i) w[i]=(k[i]=fa(i))==i;for(i=0;i^n;++i) f[i]=i;//k记录每个连通块的根,w记录每个点是否为根(缩点)
for(i=0;i^n;++i) if(w[i]) for(j=0;j^n;++j) w[j]&&p[i][j]==2&&(x=fa(i))^(y=fa(j))&&(f[x]=y);//把2在并查集上合并
for(i=0;i^n;++i) for(j=0;j^n;++j) if(i^j&&p[i][j]^2&&fa(k[i])==fa(k[j])) return 0;//判断是否存在矛盾
for(i=0;i^n;++i) w[i]&&fa(i)^i&&(b[k[fa(i)]][i]=b[i][k[fa(i)]]=1,k[fa(i)]=i,++c[fa(i)]);//k记录上次连边的点,建环
for(i=0;i^n;++i) if(w[i]&&fa(i)==i&&k[i]^i) {if(c[i]==1) return 0;b[k[i]][i]=b[i][k[i]]=1;}//如果存在两个点的环则无解,否则补全环
return build(b),1;
}