本文转载,出处:http://www.cnblogs.com/Findxiaoxun/articles/3398075.html
很巧妙的01背包升级。看完题目以后很明显有背包的感觉,然后就往背包上靠。把s看成是空间,f看成是价值,转换成了01背包经典模型(没有想到,,,)。可,s是负值,这就涉及到一个问题,如果按照普通的01背包,(01背包的倒序原因请参看这个http://hi.baidu.com/findxiaoxun/item/9abf560127a155c091571868)
for(int i=0;i<n;i++) for(int v=maxv;v>=vi[i];v--) dp[v]=max{dp[v],dp[v-vi[i]]+w[i]}
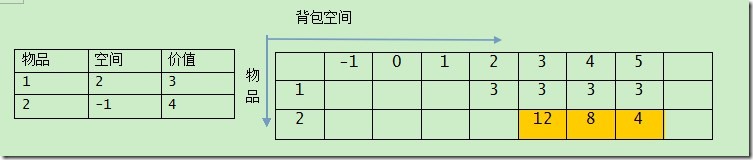
循环物品的时候,看第一件,在此题中,我们先假设最大空间为5,则2->5的值都为3,
然后i=1,循环第二件,v=5->3,而dp[5]=max{dp[5],dp[5+1]+4},背包空间为6的位置,我们假设预置为0,则dp[5]=4;dp[4]=max{dp[4],dp[4-(-1)]+4};则dp[4]=4+4=8;其实到这个值,我们已经看出,如果按照正常的逆序,s为负值的物品不只使用一次,这与题目的要求是相悖的。那么,正序考虑。读者可以自行推导,证明其可行性。
而我们发现,背包空间出现了负值,下限是-100*1000;上限是100*1000;一个很容易想到的方法就是,把100*1000,作为我们的数轴上的0点。也就是背包空间变成2*100*1000,不过在考虑的时候,以100*1000为原点,左边实际上是负值,右边是正值。则dp[i]是数据中左边一列s的和为s时的最大f值,而s+f=dp[i]+i-10000;
初始预置为-INF,dp[orgpoint]=0的目的是为了从0原点开始,而且,只放可以放的点。用一两个样例思考下就能明白。
算法的可行性,其实最大的要求就是符合01背包的特点,每个物品后只有一件,只放一次。
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int MAXN=105; const int INF=0x3f3f3f3f; const int MAXV=2*(int)1e5; int dp[MAXV+5]; int s[MAXN],f[MAXN]; int n; int main(){ int orgpoint=(int)1e5; while(scanf("%d",&n)!=EOF){ for(int i=0;i<n;i++)scanf("%d%d",&s[i],&f[i]); for(int i=0;i<=MAXV;i++)dp[i]=-INF; dp[orgpoint]=0; for(int i=0;i<n;i++){ if(s[i]>0){//>0 then in reversed order for(int j=MAXV;j>=s[i];j--)//this order ensure that we put every item just for one time if(dp[j-s[i]]>-INF) dp[j]=max(dp[j],dp[j-s[i]]+f[i]); }else{//if negative number,have a look at the proof for(int j=0;j<MAXV+s[i];j++) if(dp[j-s[i]]>-INF) dp[j]=max(dp[j],dp[j-s[i]]+f[i]); } } int ans=0; for(int i=100000;i<=200000;i++) if(dp[i]>=0&&dp[i]+i-100000>ans) ans=dp[i]+i-100000; printf("%d ",ans); } return 0; }
代码参考http://www.cnblogs.com/kuangbin/archive/2012/09/14/2684929.html
最后附上本人的代码,其实差不多啦:
#include <iostream> #include <stdio.h> #include <string.h> /* AC */ using namespace std; const int INF=0x3f3f3f3f; const int maxn=105; const int V=100000; int s[maxn],f[maxn]; int dp[V*2+10]; int n; int main() { int a,b; int sum=0; scanf("%d",&n); for(int i=0;i<n;i++){ scanf("%d%d",&a,&b); s[i]=a; f[i]=b; } //memset(dp,0,sizeof(dp)); //不能为0值。。。因为f[i]有小于0的值,应该取负无穷大的值 for(int i=0;i<V*2+10;i++) dp[i]=-INF; dp[V]=0; for(int i=0;i<n;i++){ if(s[i]>=0){ for(int v=V*2;v>=s[i];v--){ //倒叙 dp[v]=max(dp[v],dp[v-s[i]]+f[i]); } } else{ for(int v=0;v<=V*2;v++){ //正序 dp[v]=max(dp[v],dp[v-s[i]]+f[i]); } } } for(int i=100000;i<=V*2;i++){ if(i-100000+dp[i]>sum && dp[i]>=0){ sum=i-100000+dp[i]; } } printf("%d ",sum); return 0; }