魔方矩阵
魔方矩阵是有相同的行数和列数,并在每行每列、对角线上的和都相等。你能构造任何大小(除了2x2)的魔方矩阵。
1.历史
魔方又称幻方、纵横图、九宫图,最早记录于我国古代的洛书。据说夏禹治水时,河南洛阳附近的大河里浮出了一只乌龟,背上有一个很奇怪的图形,古人认为是一种祥瑞,预示着洪水将被夏禹王彻底制服。后人称之为"洛书"或"河图",又叫河洛图。
南宋数学家杨辉,在他著的《续古摘奇算法》里介绍了这种方法:只要将九个自然数按照从小到大的递增次序斜排,然后把上、下两数对调,左、右两数也对调;最后再把中部四数各向外面挺出,幻方就出现了。 (摘自《趣味数学辞典》)
在西方,阿尔布雷特·丢勒于1514年创作的木雕《忧郁》是最早关于魔方矩阵的记载。有学者认为,魔方矩阵和风靡一时的炼金术有关。几个世纪以来,魔方矩阵吸引了无数的学者和数学爱好者。本杰明·富兰克林就做过有关魔方矩阵的实验。
最简单的魔方就是平面魔方,还有立体魔方、高次魔方等。对于立体魔方、高次魔方世界上很多数学家仍在研究,本文只讨论平面魔方。
每行、每列及对角线之和被称为魔术常量或魔法总和,M。
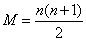
其中,n为矩阵阶数。
例如,如果n=3,则M=[3*(3^2+1)]/2 = 15.
2.魔方构造
平面魔方的一般定义:将自然数 1 到 N^2, 排列 N 行 N 列的方阵,使每行、每列及两条主对角线上的 N 个数的和都等于N (N^2+1)/2,这样的方阵称为 N 阶幻方。
通过搜索整理后,得到下面的算法:
对平面魔方的构造,分为三种情况:N为奇数、N为4的倍数、N为其它偶数(4n+2的形式)
N 为奇数时
(1) 将1放在第一行中间一列;
(2) 从2开始直到n×n止各数依次按下列规则存放:
按 45°方向行走,如向右上
每一个数存放的行比前一个数的行数减1,列数加1
(3) 如果行列范围超出矩阵范围,则回绕。
例如1在第1行,则2应放在最下一行,列数同样减1;
(4) 如果按上面规则确定的位置上已有数,或上一个数是第1行第n列时,
则把下一个数放在上一个数的下面。
N为4的倍数时
采用对称元素交换法。
首先把数1到n×n按从上至下,从左到右顺序填入矩阵
然后将方阵的所有4×4子方阵中的两对角线上的数关于大方阵中心作中心对称交换(注意是各4×4子方阵对角线上的数), 即a(i,j)与a(n-1-i,n-1-j)交换,所有其它位置上的数不变。(或者将对角线不变,其它位置对称交换也可)
N 为其它偶数时
当n为非4倍数的偶数(即4n+2形)时:首先把大方阵分解为4个奇数(2m+1阶)子方阵。
按上述奇数阶魔方给分解的4个子方阵对应赋值
上左子阵最小(i),下右子阵次小(i+v),下左子阵最大(i+3v),上右子阵次大(i+2v)
即4个子方阵对应元素相差v,其中v=n*n/4
四个子矩阵由小到大排列方式为 ① ③ ④ ②
然后作相应的元素交换:a(i,j)与a(i+u,j)在同一列做对应交换(jn-t+1),
注意其中j可以取零。
a(t-1,0)与a(t+u-1,0);a(t-1,t-1)与a(t+u-1,t-1)两对元素交换
其中u=n/2,t=(n+2)/4 上述交换使每行每列与两对角线上元素之和相等。
3.算法设计
先在矩阵第一行中间的位置上放1,然后把数字按照升序沿着左上角放置到矩阵中。如果越界了,就假设周围还有一个矩阵,将数字放到那个位置上;如果那个位置已经被占据了,就跳过该位置放到下面的位置,然后重新按照原来的方法放。如图:在5×5的魔术矩阵中,放完1以后,就把2放到1的左上角,但是此时已经越界了。假设,在原来的矩阵上面还有一个矩阵,则数字2所放的位置应该是在最后一行的第二个位置,接下去就要把数字3放到2的左上角,依次放下去,当放到6的时候,由于1已经将下一个位置占了,所以就放到5下面的位置。依照这样的规律直到把数字都放完。
4.魔方函数
Matlab中自动生成魔方矩阵的函数:
magic(n) n是矩阵维数,例如在MATLAB命令窗口输入
magic(5) ,将随机产生5阶魔方阵。
>> magic(4)
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1