该系列博客的目的是为了学习一遍数据结构中常用的概念以及常用的算法,为笔试准备;主要学习过程参考王道的《2018年-数据结构-考研复习指导》;
已总结章节:
该篇文章是有关数据结构与算法的绪论部分,主要介绍以下三个要点:
- 数据结构中相关的概念与术语;
- 数据结构三要素:逻辑结构、物理结构、数据运算;
- 算法的时间复杂度和空间复杂度;
知识框架图如下:
1. 数据结构的基本概念
1.1 基本概念和术语
数据:
数据是信息的载体,是描述客观事物属性的数、字符以及所有可能输入到计算机中并被计算机程序识别和处理的符号的集合;
数据元素:
数据元素是数据的基本单位;由若干个数据项(数据元素中不可分割的最小单位)组成;
数据对象:
数据对象是具有相同性质的数据元素的集合,是数据的一个子集;
数据类型:
数据类型是一个值的集合和定义在该集合上的一组操作的总称;
- 原子类型:其值不可再分;
- 结构类型:其值可再分;
- 抽象数据类型:抽象数据组织和与之相关的操作;
抽象数据类型(Abstract Data Type, ADT):
指一个数学模型以及定义在该模型上的一组操作;仅却决于其数学特性,与计算机内部如何实现无关;
利用数据对象、数据关系、基本操作集三元组表示抽象数据类型;
数据结构:
数据元素之间的关系,称为结构;
数据结构是数据元素的集合,并且集合内数据元素相互之间存在一种或多种特定的关系;
数据结构包含三个方面的内容(逻辑结构与存储结构密不可分):
- 逻辑结构:算法的设计取决于选定的逻辑结构;
- 存储结构:算法的实现依赖于所采用的存储结构;
- 数据的运算:
1.2 数据结构的三要素
上文提到数据结构的三要素分别为:逻辑结构、存储结构、数据的运算,下面具体介绍;
1.2.1 逻辑结构
我们先来看一下定义:逻辑结构就是指数据元素之间的逻辑关系,即从逻辑上来描述数据。
上文提到数据结构是数据元素的集合,且该集合内的数据元素相互之间存在一种或多种特定的关系;因此,可以想到,数据元素之间的这种特定关系肯定很重要;而这里的逻辑结构就是用来描述这种特定关系的;
逻辑结构独立于计算机;显而易见,逻辑结构描述的是数据元素之间的关系,现在与计算机还搭不上边;
逻辑结构描述数据元素之间的关系,那么数据元素之间不同的关系,就有着不同的逻辑结构;这里,将逻辑结构分为线性结构与非线性结构,具体见下图所示:
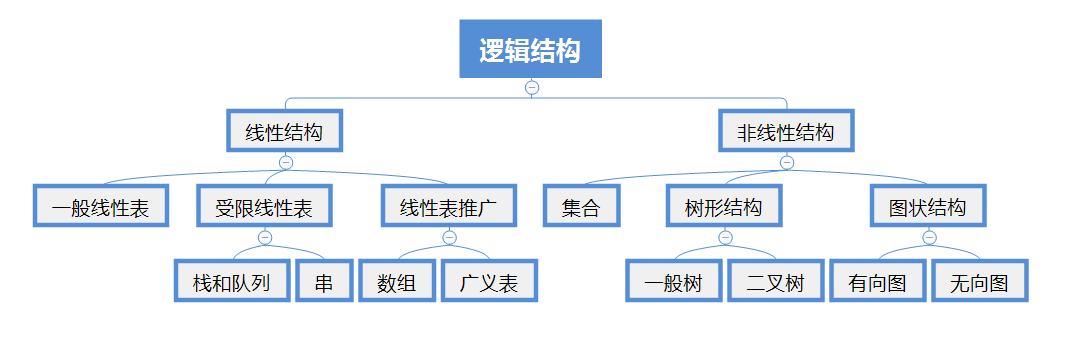
下面介绍一下常用的逻辑结构中数据元素的关系是什么样的?
- 集合:该结构中的数据元素之间除了同属于一个集合外,无其他任何关系;
- 线性结构:结构中的数据元素之间只存在一对一的关系;
- 树形结构:结构中的数据元素之间存在一对多的关系;
- 图形结构或网状结构:结构中的数据元素之间存在多对多的关系;
1.2.2 存储结构(物理结构)
同样,先看一下存储结构的定义:存储结构是指数据结构在计算机中的表示,也称物理结构;
由定义看出,存储结构应包含两个方面的内容:数据元素的表示以及数据元素之间关系的表示;
为什么这么说呢?想一下,定义中说存储结构是数据结构在计算机中的表示,而前文中数据结构的定义是数据元素的集合,且集合中的数据相互之间存在某种特定关系,因此,可以想明白存储结构包含数据元素在计算机中的表示以及数据元素之间的关系在计算机中的表示这两个方面的内容;因此呢,就可以有这样一句话:数据的存储结构是逻辑结构用计算机语言的实现。(好像还挺乱的,其实,这些概念环环相套,一层一层的理解就可以了)
那么,在计算机中,数据的存储结构有几种形式呢?我们知道,存储结构表示的意思:就是数据元素以及数据元素之间的关系在计算机中是如何表示的,而这两块内容(元素、元素关系)表示方式的不同,就有了不同的存储结构:顺序存储、链接存储、索引存储、散列存储;下面将具体介绍:
顺序存储:
将逻辑上相邻的元素存储在物理位置上也相邻的存储单元里,元素之间的关系由存储单元的邻接关系来表示;
- 优点:可以实现随机存取,每个元素占用最少的存储空间;
- 缺点:只能使用相邻的一整块存储单元,因此可能产生较多的外部碎片;
链接存储:
不要求逻辑上相邻的元素在物理位置上也相邻,借助指示元素的存储地址的指针表示元素之间的逻辑关系;
- 优点:不会出现碎片现象,充分利用所有存储单元;
- 缺点:每个元素因存储指针而占用额外的存储空间,并且该存储指针只能实现顺序存取;
索引存储:
在存储元素信息的同时,还建立附加的索引表。索引表中每一项称为索引项,索引项的一般形式是:(关键字,地址);
- 优点:检索速度快;
- 缺点:增加了附加的索引表,会占用较多的存储空间;另外,在修改索引表的时候,会很耗时;
散列存储:
根据元素的关键字直接计算出该元素的存储地址,又称Hash存储。
什么意思呢?就是说数据元素的关键字能够使用某种特定方法,计算出来的哈希(二进制的),就表示该元素的存储地址;很明显,不同的关键字要映射称不同的哈希,这样才能够保证其可用性;而这里的“映射”就表示上面所说的某种特定方法。
- 优点:检索、增加和删除节点的操作都很快;
- 缺点:如果散列函数(上面提到的“映射”以及“某种特定方法”)不好,可能会出现元素存储单元的冲突,而解决这种冲突会增加时间和空间开销;
1.2.3 数据的运算
看一下定义:施加在数据上的运算包括运算的定义和实现。
- 运算的定义是针对逻辑结构的,指出运算的功能;
- 运算的实现是针对存储结构的,指数运算的具体步骤;
2. 算法和算法评价
2.1 算法的基本概念
定义:算法(Algorithm)是对特定问题求解步骤的一种描述,它是指令的有限序列,每一条指令表示一个或多个操作。
- 目的:求解特定问题;
- 本质:一种描述;
- 表现形式:指令的有限序列;
一个算法要具有5个重要的特性:
- 有穷性:有限的步骤、有限的执行时间;
- 确定性:每条指令都有明确的含义;
- 可行性:算法的操作是在已经实现的基本运算执行有限次来实现的;
- 输入:零个或多个输入;
- 输出:一个或多个输出;
一个好的算法,应具有:
- 正确性:能够正确地解决问题;
- 可读性:良好的可读性;
- 健壮性:对于非法数据,有着良好的反应或处理能力;
- 效率高与低存储量:高效率,低存储;
2.2 算法效率的度量
2.2.1 时间复杂度
一个语句的频度指该语句在算法中出现的次数,而算法中所有语句的频度之和T(n),白哦是算法问题规模n的函数;
时间复杂度是用来分析T(n)的数量级。
一般算法中最基本运算(最深层循环内的语句)的频度与T(n)同数量级,因此使用基本运算的频度f(n)来分析时间复杂度;
其中,(O)表示T(n)的数量级;
一般满足:
其中,(C)是一个正常数;
- 最坏时间复杂度;
- 平均时间复杂度
- 最好时间复杂度
一般都是考虑最坏时间复杂度,以保证算法的运行时间不会比它更长;
加法规则:
惩罚规则:
常见的时间复杂度:
2.2.2 空间复杂度
空间复杂度定义为算法所耗费的存储空间,也是问题规模的n的函数;
原地工作是指算法所需辅助空间是常量,即(O(1));
3. 扩展
3.1 斐波那契数列的递归与非递归实现
注意:存在多种形式的数列形式,即初始值不同,需要修改下面对应位置出的代码;
3.1.1 递归实现
# python
def fib(n):
if n <= 1:
return n
else:
return fib(n-1) + fib(n-2)
3.1.2 非递归实现
# python
def fib_1(n):
if n <= 1:
return n
else:
f1 = 0
f2 = 1
c = 0
for i in range(n-1):
c = f1 + f2
f1 = f2
f2 = c
return c