该篇博客主要参考:博客园-ls秦-七大查找算法(Python);部分内容有些修改;
主要包括查找算法:顺序查找、二分查找、差值查找、分块查找;
1.查找算法——简介
查找(Searching):就是根据给定的某个值,在查找表中确定一个关键字等于给定值的数据元素;
查找表(Search Table):由同一类型的数据元素构成的集合;
关键字(Key):数据元素中某个数据项的值,又称为键值;
主键(Primary Key):可唯一的标识某个数据元素或记录的关键字;
查找表按照操作方式可分为:
1. 静态查找表(Static Search Table): 只做操作操作的查找表,主要操作:
- 查询某个特定的数据元素是否在表中;
- 检索某个特定的苏剧元素和各种属性;
2. 动态查找表(Dynamic Search Table):在查找的同时进行插入或删除等操作:
- 查找时插入数据;
- 查找时删除数据;
2. 顺序查找
算法简介:
顺序查找又称线性查找,是一种最简单的查找方法;适用于线性表的顺序村粗结构和链式存储结构;
算法的时间复杂度为(O(n));
基本思路:
从第一个元素m开始逐个与需要查找的元素x进行比较,当比较到元素值相同(m=x)时,返回元素m的下标,如果比较到最后没有找到,则返回-1;
优缺点:
- 优点:对表中数据存储没有要求。另外,对于线性链表,只能进行顺序查找;
- 缺点:当n很大时,平均查找长度较大,效率低;
算法实现:
# -*- utf-8 -*-
# @Time: 2019-04-16
# @ Author: chen, lsqin
def sequential_search(li, key):
"""顺序查找
查找数组li中指定元素key,存在返回其位置,不存在返回-1
Arguement:
li: list
查找表
key: int or str...
待查找元素
Return:
index or -1:
"""
for i in range(len(li)):
if li[i] == key:
return i
return -1
if __name__ == '__main__':
LIST = [1, 5, 8, 123, 22, 54, 7, 99, 300, 222]
result = sequential_search(LIST, 123)
print(result)
3. 二分查找
算法简介:
二分查找(Binary Search),也称折半查找,是一种在有序数组中查找某一特定元素的查找算法;
查找过程从数组的中间元素开始,如果中间元素的值等于待查找元素的值,则返回其位置,查找算法结束。如果待查找元素的值大于或者小于中间元素的值,则在数组的右半部分或则左半部分继续查找;再将左/右半个部分的中间元素的值与待查找元素的值相比较,重复上述步骤,直至找到,返回其位置,否则返回-1,查找算法结束。
算法描述:
在给定的有序数组A中查找元素key;
Step 1:利用(low, high)分别表示当前查找表的下界和上届;
Step 2:如果(low > high),返回-1,查找算法结束;
Step 3:令(mid=lfloor dfrac{low+high}{2} floor);
Step 4:如果(A_{mid}=key),查找成功,返回(mid),查找算法结束;
Step 5:如果(A_{mid} > key),令$high=mid-1 $,回到步骤Step 2;
Step 6:如果(A_{mid} < key),令$low=mid+1 $,回到步骤Step 2;
复杂度分析:
时间复杂度:折半搜索每次把搜索区域减少一半,时间复杂度为(O(log n));
空间复杂度为(O(1));
算法实现:
def binary_search(li, key):
"""折半查找
在给定的有序数组中查找指定元素,
查找成功,则返回待查找元素在有序数组中的位置,以及比较次数
查找失败,则返回-1,以及比较次数
Argument:
li: list
有序数组
kye: int
待查找元素
Return:
index: int
位置索引或-1
"""
low = 0
high = len(li) - 1
time = 0 # 比较的次数
while low < high:
time += 1
mid = int((low + high) / 2)
if li[mid] == key:
print("times: %s" % time)
return mid
elif li[mid] > key:
high = mid - 1
else:
low = mid + 1
print("times: %s" % time)
return -1
if __name__ == '__main__':
LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
loc = binary_search(LIST, 99)
print('loc: ', loc)
4.插值查找
算法简介:
插值查找类似于二分查找,同样对给定的查找表是有序数组;不同的是,与待查元素相比较的待查表中元素的选择方式不同;在二分查找中,待比较元素是有序数组的中间元素;在插值查找中,通过下述公式计算待比较元素在有序数组中的位置:
算法思想:
差值查找也属于有序查找,基于二分查找算法,将查找点的选择改为自适应选择,可以提高查找效率;
对于表长较大,而关键字分布比较均匀的查找表来说,差值查找算法的平均性能优于二分查找;相反,如果数组关键字分布不均匀,那么插值查找算法未必是很合适的选择。
复杂度分析:
时间复杂度:如果元素分布均匀,时间复杂度为(O(log n));最坏情况下,**时间复杂度为(O(n));
空间复杂度:(O(1));
算法实现:
# -*- utf-8 -*-
# @Time: 2019-04-16
# @ Author: chen, lsqin
def binary_search(li, key):
"""插值查找
在给定的有序数组中查找指定元素,
查找成功,则返回待查找元素在有序数组中的位置,以及比较次数
查找失败,则返回-1,以及比较次数
Argument:
li: list
有序数组
kye: int
待查找元素
Return:
index: int
位置索引或-1
"""
low = 0
high = len(li) - 1
time = 0
while low < high:
time += 1
# 计算待比较元素在有序数组中的位置
loc = low + int((high - low) * (key - li[low]) / (li[high] - li[low]))
print("mid=%s, low=%s, high=%s" % (loc, low, high))
if li[loc] == key:
print("times: %s" % time)
return loc
elif li[loc] > key:
high = loc - 1
else:
low = loc + 1
print("times: %s" % time)
return -1
if __name__ == '__main__':
LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
result = binary_search(LIST, 444)
print(result)
5. 斐波那契查找
算法简介:
斐波那契数列,又称黄金分割数列,该数列越往后相邻的两个数的比值越趋近于0.618;如下:
算法描述:
斐波那契查找也类似于二分查找,在给定的有序数组中查找指定元素;不同的是,斐波那契查找的拆分点的选择方式是根据斐波那契数列得来的;即采用最接近查找表长度的斐波那契数值来确定拆分点;
那么上面那句话到底是个什么意思呢?具体如下:
给定一个有序查找表A:
Step 1:确定查找表的长度为(n_1);
Step 2:找到一个不小于(n)的最小斐波那契数(F(k));其中,(k)表示斐波那契数列中的第(k)个值;
Step 3:对查找表扩展,使新的查找表B的长度为(n_2 = F(k)-1);(这里不明白)
Step 4:对扩展查找表进行拆分,拆分点在扩展查找表中的索引位置为:(loc = F(k-1)-1);
Step 5:将拆分点的值与待查找元素相比较;
Step 6:如果找到,算法结束;
- 如果(A[loc] > key),则将(k=k-1);
- 如果(A[loc] < key),则将(k=k-2);
复杂度分析:
最坏的情况下,时间复杂度为(O(log n));
算法实现:
# -*- utf-8 -*-
# @Time: 2019-04-16
# @ Author: chen, lsqin
def fibonacci(n):
"""斐波那契数列
Argument:
n: int
Return:
斐波那契数
"""
if n == 0 or n == 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
def fibonacci_search(li, key):
"""斐波那契查找
在给定的有序数组中查找指定元素,
查找成功,则返回待查找元素在有序数组中的位置,以及比较次数
查找失败,则返回-1,以及比较次数
Argument:
li: list
有序数组
kye: int
待查找元素
Return:
index: int
位置索引或-1
"""
low = 0 # 查找表上界
high = len(li) - 1 # 查找表下界
# Step 1
length = high + 1 # 查找表长度
# Step 2
k = 0 # 斐波那契数索引
while True:
num_fibonacci = fibonacci(k)
if num_fibonacci > length:
break
k += 1
# Step 3: 扩展查找表
expansion_li = li
for i in range(num_fibonacci - length - 1):
expansion_li.append(li[-1])
print('new search table: ', expansion_li)
# Step 4
time = 0
while low < high:
# 防止F列表下标溢出
if k < 2:
loc = low
else:
loc = low + fibonacci(k - 1) - 1
s
time += 1
loc = low + fibonacci(k - 1) - 1 # 拆分点在扩展查找表中的索引位置
if expansion_li[loc] == key:
print("times: %s" % time)
return loc
elif expansion_li[loc] > key:
high = loc - 1
k -= 1
else:
low = loc + 1
k -= 2
print("times: %s" % time)
return -1
if __name__ == '__main__':
LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444, 555, 666]
result = fibonacci_search(LIST, 444)
print('index:', result)
6. 分块查找
算法简介:
分块查找,又称为索引顺序查找,吸取了顺序查找和折半查找各自的优点,既有动态结构,又适于快速查找;
算法思想:
将查找表分成若干个子块:块内元素可以无序,块间元素有序;即第一个块的所有元素小于第二个块的任一元素...
构建一个索引表:索引表中含有各块的最大关键字和各块第一个元素的地址,如下图;
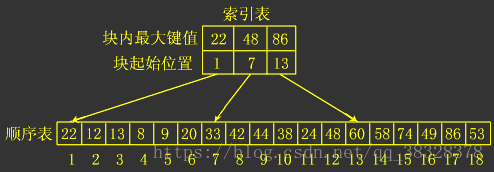
算法流程:
Step 1:先选取各块中的最大关键字构成一个索引表;
Step 2:查找分为两个部分:首先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中;
Step 3:其次,在已确定的块中用顺序查找算法进行查找;
复杂度分析:
时间复杂度为(O(log m + N/m));(m)表示分块的个数;