A - 数列分块入门 1
分块模板题:lazy[i] 表示第i块整体的更新量
单点询问:res = a[x] + lazy[belong[x]]

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(int i = a;i <= b;i++) #define bep(i,a,b) for(int i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 1e9 + 7; inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } int sz; int a[maxn], belong[maxn], lazy[maxn]; int b[maxn], tag[maxn], val[maxn]; int L[maxn], R[maxn]; int n; void add(int l, int r, int c) { if (belong[l] == belong[r]) { rep(i, l, r)a[i] += c; } else { rep(i, belong[l] + 1, belong[r] - 1)lazy[i] += c; rep(i, l, R[belong[l]])a[i] += c; rep(i, L[belong[r]] , r)a[i] += c; } } int query(int x) { return a[x] + lazy[belong[x]]; } int main() { n = read(); sz = sqrt(n); rep(i, 1, n)a[i] = read(); rep(i, 1, n)belong[i] = (i - 1) / sz + 1; int num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, n); L[i] = l, R[i] = r; } rep(i, 1, n) { int op, l, r, c; op = read(), l = read(), r = read(), c = read(); if (op == 0)add(l, r, c); else { cout << query(r) << endl; } } return 0; }
B - 数列分块入门 2
另开数组b记录块内有序的数组a
对于整块:二分查找小于x的元素个数
对于非整块:暴力查找小于x的元素个数

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 1e9 + 7; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } struct node { int x, id; bool operator < (const node& r)const { return x < r.x || (x == r.x && id < r.id); } }; int cmp1(node aa, node b) { return aa.x < b.x; } int cmp2(node aa, node b) { return aa.id < b.id; } int sz; ll belong[maxn], lazy[maxn]; ll a[maxn], b[maxn]; int L[maxn], R[maxn]; int n; void add(int l, int r, ll c) { if (belong[l] == belong[r]) { rep(i, l, r)a[i] += c; rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; sort(b + L[belong[l]], b + 1 + R[belong[l]]); } else { rep(i, belong[l] + 1, belong[r] - 1)lazy[i] += c; rep(i, l, R[belong[l]])a[i] += c; rep(i, L[belong[r]], r)a[i] += c; rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; rep(i, L[belong[r]], R[belong[r]])b[i] = a[i]; sort(b + L[belong[l]], b + 1 + R[belong[l]]); sort(b + L[belong[r]], b + 1 + R[belong[r]]); } } int query(int l, int r, ll x) { int sum = 0; if (belong[l] == belong[r]) { rep(i, l, r) { if (a[i] + lazy[belong[i]] < x)sum++; } } else { rep(i, l, R[belong[l]]) { if (a[i] + lazy[belong[i]] < x)sum++; } rep(i, L[belong[r]], r) { if (a[i] + lazy[belong[i]] < x)sum++; } rep(i, belong[l] + 1, belong[r] - 1) { //int pos = Find(L[i], R[i], x - lazy[i]); sum += lower_bound(b + L[i], b + 1 + R[i], x - lazy[i]) - b - L[i]; } } return sum; } int main() { //cout << 50000 * sqrt(50000) * log(sqrt(50000)) << endl; n = read(); sz = sqrt(n); rep(i, 1, n)belong[i] = (i - 1) / sz + 1; rep(i, 1, n) { a[i] = read(); b[i] = a[i]; } int num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, (ll)n); L[i] = l, R[i] = r; sort(b + l, b + 1 + r); } rep(i, 1, n) { ll op, l, r, c; op = read(), l = read(), r = read(), c = read(); if (op == 0)add(l, r, c); else { cout << query(l, r, c * c) << endl; } } return 0; } /* 5 1 5 9 6 2 0 1 5 1 1 1 5 9 1 1 5 3 */
C - 数列分块入门 3
和入门2差不多,整块二分,非整块暴力

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 1e9 + 7; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; ll belong[maxn], lazy[maxn]; ll a[maxn], b[maxn]; int L[maxn], R[maxn]; int n; void add(int l, int r, ll c) { if (belong[l] == belong[r]) { rep(i, l, r)a[i] += c; rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; sort(b + L[belong[l]], b + 1 + R[belong[l]]); } else { rep(i, belong[l] + 1, belong[r] - 1)lazy[i] += c; rep(i, l, R[belong[l]])a[i] += c; rep(i, L[belong[r]], r)a[i] += c; rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; rep(i, L[belong[r]], R[belong[r]])b[i] = a[i]; sort(b + L[belong[l]], b + 1 + R[belong[l]]); sort(b + L[belong[r]], b + 1 + R[belong[r]]); } } int query(int l, int r, ll x) { ll res = -1; if (belong[l] == belong[r]) { rep(i, l, r) { if (a[i] + lazy[belong[i]] < x) { res = max(res, a[i] + lazy[belong[i]]); } } } else { rep(i, l, R[belong[l]]) { if (a[i] + lazy[belong[i]] < x) { res = max(res, a[i] + lazy[belong[i]]); } } rep(i, L[belong[r]], r) { if (a[i] + lazy[belong[i]] < x) { res = max(res, a[i] + lazy[belong[i]]); } } rep(i, belong[l] + 1, belong[r] - 1) { int pos = lower_bound(b + L[i], b + 1 + R[i], x - lazy[i]) - b; if (pos != L[i])res = max(res, b[pos-1] + lazy[i]); } } return res; } int main() { n = read(); sz = sqrt(n); rep(i, 1, n)belong[i] = (i - 1) / sz + 1; rep(i, 1, n) { a[i] = read(); b[i] = a[i]; } int num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, (ll)n); L[i] = l, R[i] = r; sort(b + l, b + 1 + r); } rep(i, 1, n) { ll op, l, r, c; op = read(), l = read(), r = read(), c = read(); if (op == 0)add(l, r, c); else { cout << query(l, r, c) << endl; } } return 0; } /* 5 1 5 9 6 2 0 1 5 1 1 1 5 9 1 1 5 3 */
D - 数列分块入门 4
lazy[i] 表示第i块的更新量
sum[i] 代表第i块的和
区间求和:
整块:res += sum[belong[x]] + sz * lazy[belong[x]]
非整块:res += a[x] + lazy[belong[x]]

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 1e9 + 7; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; ll belong[maxn], lazy[maxn],sum[maxn]; ll a[maxn], b[maxn]; int L[maxn], R[maxn]; int n; void add(int l, int r, ll c) { if (belong[l] == belong[r]) { rep(i, l, r) { a[i] += c; sum[belong[l]] += c; } //rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; //sort(b + L[belong[l]], b + 1 + R[belong[l]]); } else { rep(i, belong[l] + 1, belong[r] - 1)lazy[i] += c; rep(i, l, R[belong[l]]) { a[i] += c; sum[belong[l]] += c; } rep(i, L[belong[r]], r) { a[i] += c; sum[belong[r]] += c; } /*rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; rep(i, L[belong[r]], R[belong[r]])b[i] = a[i]; sort(b + L[belong[l]], b + 1 + R[belong[l]]); sort(b + L[belong[r]], b + 1 + R[belong[r]]);*/ } } int query(int l, int r, ll x) { ll res = 0; if (belong[l] == belong[r]) { rep(i, l, r) { res = (res + a[i] + lazy[belong[i]]) % x; } } else { rep(i, l, R[belong[l]]) { res = (res + a[i] + lazy[belong[i]]) % x; } rep(i, L[belong[r]], r) { res = (res + a[i] + lazy[belong[i]]) % x; } rep(i, belong[l] + 1, belong[r] - 1) { res = (res + sum[i] + sz * lazy[i]) % x; } } return res; } int main() { n = read(); sz = sqrt(n); rep(i, 1, n)belong[i] = (i - 1) / sz + 1; rep(i, 1, n) { a[i] = read(); //b[i] = a[i]; } int num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, (ll)n); L[i] = l, R[i] = r; rep(j, l, r)sum[i] += a[j]; //sort(b + l, b + 1 + r); } rep(i, 1, n) { ll op, l, r, c; op = read(), l = read(), r = read(), c = read(); if (op == 0)add(l, r, c); else { cout << query(l, r, c+1) << endl; } } return 0; } /* 5 1 5 9 6 2 0 1 5 1 1 1 5 9 1 1 5 3 */
E - 数列分块入门 5
n <= 50000,每个数最多开方4次就会变为1
sum[i]数组表示第i块的和
整块:tag[i]记录第i块更新了多少次,若超过4次则啥都不干,否则暴力更新一下,记得更新sum
非整块:暴力更新
区间求和:整块用sum数组,非整块暴力求和

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 1e9 + 7; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; ll belong[maxn], lazy[maxn],sum[maxn],tag[maxn]; ll a[maxn], b[maxn]; int L[maxn], R[maxn]; int n; void add(int l, int r, ll c) { if (belong[l] == belong[r]) { rep(i, l, r) { a[i] += c; sum[belong[l]] += c; } //rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; //sort(b + L[belong[l]], b + 1 + R[belong[l]]); } else { rep(i, belong[l] + 1, belong[r] - 1)lazy[i] += c; rep(i, l, R[belong[l]]) { a[i] += c; sum[belong[l]] += c; } rep(i, L[belong[r]], r) { a[i] += c; sum[belong[r]] += c; } /*rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; rep(i, L[belong[r]], R[belong[r]])b[i] = a[i]; sort(b + L[belong[l]], b + 1 + R[belong[l]]); sort(b + L[belong[r]], b + 1 + R[belong[r]]);*/ } } void update(int l, int r) { if (belong[l] == belong[r]) { rep(i, l, r) { ll x = sqrt(a[i]); sum[belong[i]] -= a[i] - x; a[i] = x; } } else { rep(i, l, R[belong[l]]) { ll x = sqrt(a[i]); sum[belong[i]] -= a[i] - x; a[i] = x; } rep(i, L[belong[r]], r) { ll x = sqrt(a[i]); sum[belong[i]] -= a[i] - x; a[i] = x; } rep(i, belong[l] + 1, belong[r] - 1) { if (tag[i] > 4)continue; else { tag[i]++; rep(j, L[i], R[i]) { ll x = sqrt(a[j]); sum[i] -= a[j] - x; a[j] = x; } } } } } int query(int l, int r) { ll res = 0; if (belong[l] == belong[r]) { rep(i, l, r) { res += a[i]; } } else { rep(i, l, R[belong[l]]) { res += a[i]; } rep(i, L[belong[r]], r) { res += a[i]; } rep(i, belong[l] + 1, belong[r] - 1) { res += sum[i]; } } return res; } int main() { n = read(); sz = sqrt(n); rep(i, 1, n) belong[i] = (i - 1) / sz + 1; rep(i, 1, n) a[i] = read(); int num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, (ll)n); L[i] = l, R[i] = r; rep(j, l, r)sum[i] += a[j]; } rep(i, 1, n) { ll op, l, r, c; op = read(), l = read(), r = read(), c = read(); if (op == 0)update(l, r); else { cout << query(l, r) << endl; } } return 0; } /* 5 1 5 9 6 2 0 1 5 1 1 1 5 9 1 1 5 3 */
F - 数列分块入门 6
初始sqrt(n)分块,若插入后某块的元素个数大于sqrt(2*n),便将该块进行一分为二
插入用vector进行插入

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 10007; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; int belong[maxn], prod[maxn],sum[maxn],tag[maxn]; int a[maxn], b[maxn],val[maxn],vis[maxn]; int L[maxn], R[maxn]; int cnt[maxn]; int n,num,up; vector<int>v[maxn]; void divide(int id) { bep(i, num + 1, id+2)v[i] = v[i - 1]; int x1 = SZ(v[id]) / 2, x2 = SZ(v[id]) - x1; v[id + 1].clear(); for (int i = x1; i < SZ(v[id]); i++)v[id + 1].push_back(v[id][i]); while (SZ(v[id]) > x1)v[id].pop_back(); num++; } void Insert(int pos, int x) { //pos前插入x rep(i, 1, num) { if (pos > SZ(v[i])) { pos -= SZ(v[i]); } else { v[i].insert(v[i].begin() + pos - 1, x); if(SZ(v[i]) > up)divide(i); return; } } } int query(int x) { //a[x] int ans = 0; rep(i, 1, num) { if (x > SZ(v[i])) { x -= SZ(v[i]); } else { ans = v[i][x-1]; break; } } return ans; } int main() { n = read(); sz = sqrt(n); up = sqrt(n * 2); rep(i, 1, n) { belong[i] = (i - 1) / sz + 1; a[i] = read(); } num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, (ll)n); L[i] = l, R[i] = r; rep(j, L[i], R[i]) { v[i].push_back(a[j]); } } rep(i, 1, n) { int op, l, r, c; op = read(), l = read(), r = read(), c = read(); if (op == 0)Insert(l, r); else cout << query(r) << endl; } return 0; } /* */
G - 数列分块入门 7
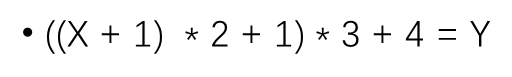

上述Y分成前后两部分
prod[i]代表第i块的前半部分,sum[i]代表第i块的右半部分
单点询问:res = a[x] * prod[belong[x]] + sum[belong[x]]

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 10007; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; int belong[maxn], prod[maxn],sum[maxn],tag[maxn]; int a[maxn], b[maxn]; int L[maxn], R[maxn]; int n; int query(int x) { return (a[x] * prod[belong[x]] + sum[belong[x]])% mod; } void add(int l, int r, int c) { if (belong[l] == belong[r]) { rep(i, L[belong[l]], R[belong[l]]) { a[i] = query(i); if (i >= l && i <= r)a[i] = (a[i] + c) % mod; } sum[belong[l]] = 0; prod[belong[l]] = 1; } else { rep(i, L[belong[l]], R[belong[l]]) { a[i] = query(i); if (i >= l && i <= R[belong[l]])a[i] = (a[i] + c) % mod; } rep(i, L[belong[r]], R[belong[r]]) { a[i] = query(i); if (i >= L[belong[r]] && i <= r)a[i] = (a[i] + c) % mod; } sum[belong[l]] = sum[belong[r]] = 0; prod[belong[l]] = prod[belong[r]] = 1; rep(i, belong[l] + 1, belong[r] - 1)sum[i] = (sum[i] + c) % mod; } } void mul(int l, int r,int c) { if (belong[l] == belong[r]) { rep(i, L[belong[l]], R[belong[l]]) { a[i] = query(i); if (i >= l && i <= r)a[i] = a[i] * c % mod; } sum[belong[l]] = 0; prod[belong[l]] = 1; } else { rep(i, L[belong[l]], R[belong[l]]) { a[i] = query(i); if (i >= l && i <= R[belong[l]])a[i] = (a[i] * c) % mod; } rep(i, L[belong[r]], R[belong[r]]) { a[i] = query(i); if (i >= L[belong[r]] && i <= r)a[i] = (a[i] * c) % mod; } sum[belong[l]] = sum[belong[r]] = 0; prod[belong[l]] = prod[belong[r]] = 1; rep(i, belong[l] + 1, belong[r] - 1) { prod[i] = prod[i] * c % mod; sum[i] = sum[i] * c % mod; } } } int main() { n = read(); sz = sqrt(n); rep(i, 1, n) belong[i] = (i - 1) / sz + 1; rep(i, 1, n) { a[i] = read(); a[i] %= mod; } int num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, (ll)n); L[i] = l, R[i] = r; prod[i] = 1; } rep(i, 1, n) { int op,l, r, c; op = read(),l = read(), r = read(), c = read(); c %= mod; if (op == 0)add(l, r, c); else if (op == 1)mul(l, r, c); else if (op == 2)cout << query(r) << endl; /* rep(j, 1, n)cout << query(j) << ' '; cout << endl; rep(j, 1, n)cout << a[j] << ' '; cout << endl; rep(j, 1, num)cout << sum[j] << ' '; cout << endl; rep(j, 1, num)cout << prod[j] << ' '; cout << endl;*/ } return 0; } /* 5 1 2 3 5 4 0 1 5 1 0 1 5 1 1 1 5 2 0 1 5 4 1 1 5 2 */
H - 数列分块入门 8
tag[i]标记第i块内是否全为同一个值

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 1e9 + 7; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; ll belong[maxn], lazy[maxn],sum[maxn],tag[maxn]; ll a[maxn], b[maxn]; int L[maxn], R[maxn]; int n; void add(int l, int r, ll c) { if (belong[l] == belong[r]) { rep(i, l, r) { a[i] += c; sum[belong[l]] += c; } //rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; //sort(b + L[belong[l]], b + 1 + R[belong[l]]); } else { rep(i, belong[l] + 1, belong[r] - 1)lazy[i] += c; rep(i, l, R[belong[l]]) { a[i] += c; sum[belong[l]] += c; } rep(i, L[belong[r]], r) { a[i] += c; sum[belong[r]] += c; } /*rep(i, L[belong[l]], R[belong[l]])b[i] = a[i]; rep(i, L[belong[r]], R[belong[r]])b[i] = a[i]; sort(b + L[belong[l]], b + 1 + R[belong[l]]); sort(b + L[belong[r]], b + 1 + R[belong[r]]);*/ } } void update(int l, int r) { if (belong[l] == belong[r]) { rep(i, l, r) { ll x = sqrt(a[i]); sum[belong[i]] -= a[i] - x; a[i] = x; } } else { rep(i, l, R[belong[l]]) { ll x = sqrt(a[i]); sum[belong[i]] -= a[i] - x; a[i] = x; } rep(i, L[belong[r]], r) { ll x = sqrt(a[i]); sum[belong[i]] -= a[i] - x; a[i] = x; } rep(i, belong[l] + 1, belong[r] - 1) { if (tag[i] > 4)continue; else { tag[i]++; rep(j, L[i], R[i]) { ll x = sqrt(a[j]); sum[i] -= a[j] - x; a[j] = x; } } } } } int query(int l, int r,ll c) { ll res = 0; if (belong[l] == belong[r]) { if (tag[belong[l]] == INF) { rep(i, l, r) { if (a[i] == c)res++; else a[i] = c; } } else if(tag[belong[l]] == c){ res = r - l + 1; } else { res = 0; rep(i, L[belong[l]], R[belong[l]]) { if (i >= l && i <= r)a[i] = c; else a[i] = tag[belong[i]]; } tag[belong[l]] = INF; } } else { if (tag[belong[l]] == INF) { rep(i, l, R[belong[l]]) { if (a[i] == c)res++; else a[i] = c; } } else if (tag[belong[l]] == c) { res += R[belong[l]] - l + 1; } else { res += 0; rep(i, L[belong[l]], R[belong[l]]) { if (i >= l && i <= R[belong[l]])a[i] = c; else a[i] = tag[belong[i]]; } tag[belong[l]] = INF; } if (tag[belong[r]] == INF) { rep(i, L[belong[r]], r) { if (a[i] == c)res++; else a[i] = c; } } else if (tag[belong[r]] == c) { res += r - L[belong[r]] + 1; } else { res += 0; rep(i, L[belong[r]], R[belong[r]]) { if (i >= L[belong[r]] && i <= r)a[i] = c; else a[i] = tag[belong[i]]; } tag[belong[r]] = INF; } rep(i, belong[l] + 1, belong[r] - 1) { if (tag[i] == INF) { rep(j, L[i], R[i]) { if (a[j] == c)res++; } tag[i] = c; } else if(tag[i] == c){ res += R[i] - L[i] + 1; } else { res += 0; tag[i] = c; } } } return res; } int main() { n = read(); sz = sqrt(n); rep(i, 1, n) belong[i] = (i - 1) / sz + 1; rep(i, 1, n) a[i] = read(); int num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, (ll)n); L[i] = l, R[i] = r; tag[i] = INF; } rep(i, 1, n) { ll l, r, c; l = read(), r = read(), c = read(); cout << query(l, r, c) << endl; } return 0; } /* 6 1 2 2 2 5 2 2 6 2 2 6 2 1 5 2 1 6 2 2 6 3 4 6 3 */
I - 数列分块入门 9
区间最小众数
mode[l][r]代表第l块到第r块的最小众数
非整块二分查找x在[l,r]出现多少次,以便更新众数

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 10007; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; int belong[maxn], prod[maxn],sum[maxn],tag[maxn]; int a[maxn], b[maxn],val[maxn],vis[maxn]; int L[maxn], R[maxn]; int mode[5050][5050]; //mode[l][r]代表 块[l,r]的众数 int cnt[maxn]; int n,num,tot; vector<int>v[maxn]; map<int, int>mp; void Init(int l) { rep(i, 1, tot)cnt[i] = 0; int res = 0, id = 0; rep(i, L[l], n) { cnt[a[i]]++; if (res < cnt[a[i]] || (res == cnt[a[i]] && val[a[i]] < val[id])) { res = cnt[a[i]]; id = a[i]; } int r = belong[i]; mode[l][r] = id; } } int Find(int l, int r, int x) {//[l,r]区间x出现多少次 int L = lower_bound(v[x].begin(), v[x].end(), l) - v[x].begin(); int R = upper_bound(v[x].begin(), v[x].end(), r) - v[x].begin(); return R-L; } int query(int l,int r) { //[l,r]最小众数 int res = 0, mx = 0; if (belong[l] == belong[r]) { rep(i, l, r) { if (!vis[a[i]]) { vis[a[i]]++; int now = Find(l, r, a[i]); if (mx < now || (mx == now && val[a[i]] < val[res])) { mx = now; res = a[i]; } } } rep(i, l, r)vis[a[i]] = 0; } else { res = mode[belong[l] + 1][belong[r] - 1]; mx = Find(l, r, res);//res(众数)出现多少次 rep(i, l, R[belong[l]]) { if (!vis[a[i]]) { vis[a[i]]++; int now = Find(l, r, a[i]); if (mx < now || (mx == now && val[a[i]] < val[res])) { mx = now; res = a[i]; } } } rep(i, L[belong[r]], r) { if (!vis[a[i]]) { vis[a[i]]++; int now = Find(l, r, a[i]); if (mx < now || (mx == now && val[a[i]] < val[res])) { mx = now; res = a[i]; } } } rep(i, l, R[belong[l]]) { vis[a[i]] = 0; } rep(i, L[belong[r]], r) { vis[a[i]] = 0; } } return val[res]; } int main() { n = read(); sz = sqrt(n); rep(i, 1, n) belong[i] = (i - 1) / sz + 1; rep(i, 1, n) { a[i] = read(); if (!mp.count(a[i])) { mp[a[i]] = ++tot; } v[mp[a[i]]].push_back(i); val[mp[a[i]]] = a[i]; a[i] = mp[a[i]]; } num = ceil(n * 1.0 / sz); rep(i, 1, num) { int l = (i - 1) * sz + 1, r = min(i * sz, (ll)n); L[i] = l, R[i] = r; Init(i); } rep(i, 1, n) { int l, r; l = read(), r = read(); cout << query(l, r) << endl; } return 0; } /* */
J - Group
分块+莫队
问:[l,r]区间连续的段有多少
首先按块从小到大排序,同块以右端点从小到大排序

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 100020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 1e9 + 7; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; struct node { int l, r, id; bool operator < (const node& w)const { return l / sz < w.l / sz || (l / sz == w.l / sz && r < w.r); } }q[maxn]; ll a[maxn],ans[maxn],sum[maxn]; ll res; void add(int x) { res++; sum[a[x]]++; if (sum[a[x] - 1])res--; if (sum[a[x] + 1])res--; } void remove(int x) { res--; sum[a[x]]--; if (sum[a[x] - 1])res++; if (sum[a[x] + 1])res++; } int main() { int T = read(); while (T--) { int n = read(),m = read(); sz = sqrt(n); rep(i, 1, n) { a[i] = read(); } rep(i, 1, n + 1)sum[i] = 0; rep(i, 1, m) { q[i].l = read(), q[i].r = read(); q[i].id = i; } sort(q + 1, q + 1 + m); int L = 1, R = 0; res = 0; rep(i, 1, m) { while (R < q[i].r)add(++R); while (L > q[i].l)add(--L); while (R > q[i].r)remove(R--); while (L < q[i].l)remove(L++); ans[q[i].id] = res; } rep(i, 1, m)cout << ans[i] << endl; } return 0; }
K - D-query
分块+莫队 模板题
[l,r]区间不同的数的个数

#include<map> #include<set> #include<cmath> #include<deque> #include<queue> #include<stack> #include<string> #include<bitset> #include<cstdio> #include<vector> #include<iomanip> #include<cstring> #include<sstream> #include<iostream> #include<algorithm> #include<unordered_map> //#include<bits/stdc++.h> #define fi first #define se second #define eps 1e-8 #define ll long long #define ull unsigned long long #define pb push_back #define maxn 1000020 #define inf 0x3f3f3f3f #define INF 0x3f3f3f3f3f3f3f3f #define P pair<ll, ll> #define pi acos(-1) #define lson l,mid,rt*2 #define rson mid+1,r,rt*2+1 #define lowbit(x) (x&(-x)) #define SZ(x) ((ll)(x).size()) #define met(a,x) memset(a,x,sizeof(a)) #define openin(x) freopen(x, "r", stdin) #define openout(x) freopen(x, "w",stdout) #define rep(i,a,b) for(ll i = a;i <= b;i++) #define bep(i,a,b) for(ll i = a;i >= b;i--) #define ios() ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); using namespace std; ll mod = 1e9 + 7; ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll lcm(ll a, ll b) { return a * b / gcd(a, b); } inline ll read() { ll x = 0, sign = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') sign = -1; for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0'; return sign * x; } ll bit[111]; void Linear_basis(ll a[], int n) { rep(k, 1, n) { ll x = a[k]; bep(i, 60, 0) { if ((x >> i) & 1) {//x的第i位为1 if (bit[i])x ^= bit[i]; else { bit[i] = x; break; } } } } } ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int sz; struct node { int l, r, id; bool operator < (const node& w)const { return l / sz < w.l / sz || (l / sz == w.l / sz && r < w.r); } }q[maxn]; ll a[maxn],query[maxn],ans[maxn],sum[maxn]; ll res; void add(int x) { if (sum[a[x]] == 0)res++; sum[a[x]]++; } void remove(int x) { sum[a[x]]--; if (sum[a[x]] == 0)res--; } int main() { int n = read(); sz = sqrt(n); rep(i, 1, n)a[i] = read(); int m; cin >> m; rep(i, 1, m) { q[i].l = read(), q[i].r = read(); q[i].id = i; } sort(q + 1, q + 1 + m); int L = 1, R = 0; rep(i, 1, m) { while (R < q[i].r)add(++R); while (L > q[i].l)add(--L); while (R > q[i].r)remove(R--); while (L < q[i].l)remove(L++); ans[q[i].id] = res; } rep(i, 1, m)cout << ans[i] << endl; return 0; }
