离散数学--十一章 格与布尔代数

格的定义与性质:

布尔代数是计算机逻辑设计的基础，它是由格引出的。格又是从偏序集引出的。所以我们先回顾一下偏序集中的一些概念。

 偏序集

简单来说就是集合A中有自反，反自反，传递的关系

具体可以看第七章

我们结合Hasse图看如下关系：

假如 A={1,2,3,6,12,24,36} 且有如下关系

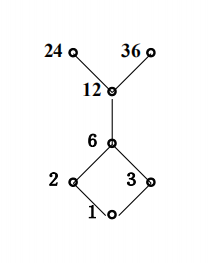
如果：B={2，3，6}

最大|小元

定义：

y是B的最小元⇔∃y∈B∧∀x(x∈B→y≤x) 

y是B的最大元⇔∃y∈B∧∀x(x∈B→x≤y)

最大|小元是唯一的（类比函数的最值）

而极大|小元不唯一

B最大元6 ，最小元无 

B中Hasse图的最底（顶）层，且这一层只有一个点才能是最小（大）元

极大|小元

定义：

y是B的极小元⇔∃y∈B∧¬∃x(x∈B∧x≤y) 

y是B的极大元⇔∃y∈B∧¬∃x(x∈B∧y≤x)  

这里面B的极小元是 {2，3}，极大元是 {6}

B中Hasse图的最底（顶）层，则是极小（大）元

上下界

定义：

y是B的下界⇔∃y∈A∧∀x(x∈B→y≤x)

y是B的上界⇔∃y∈A∧∀x(x∈B→x≤y)

比如 B上界 {12，24，36} 下界 {1}

Hasse图中B的最底（顶）层，包括这一层和这一层下面（上面）的所有元素构成的集合则是下（上）界 

确界

定义：

B的上确界（最小上界）下确界（最大下界）就是上界的min，下界的max

结合Hasse 图理解

若B={2，3，6} 有如上图的关系

格

讲这么多终于到格的定义了

其实只要一个偏序集中任意子集都有上下确界就是格了莫名很简洁

暗示判断格要疯狂枚举

格诱导的代数系统

交并运算

设<A, ≤>是格,在A上定义二元运算∨和∧为:∀a,b∈A

a∨b=LUB {a,b} |{a,b}的最小上界.Least Upper Bound

a∧b=GLB {a,b} |{a,b}的最大下界.Greatest Lower Bound

称<A,∨,∧>是由格<A,≤>诱导的代数系统. (∨-并,∧-交)

就是用符号定义了上下确界而已

并且有：设<L, ≼>是格则有运算∨和∧适合交换律、结合

律、幂等律和吸收律

<==> 设<S, ∗, ◦ >是代数系统, ∗和◦是二元运算, 如

果∗和◦满足交换律、结合律和吸收律, 则<S, ∗,◦>构成格.

注意一下吸收率就好了：

a∨(a∧b) = a, a∧(a∨b) = a

各种格

分配格

如果交并还满足分配率就叫分配格

有界格

如果B是A时仍有上下确界 则此时的格为有界格，这个确界分别称为全上|下界

一般将全上界记为1 ，全下界记为0，一般将有界格L记为<L,∧,∨,0,1>.

有限格L={a1,a2,…,an}是有界格, 则a1∧a2∧…∧an是L的全下

界, a1∨a2∨…∨an是L的全上界. 

0是关于∧运算的零元,∨运算的单位元；1是关于∨运算的

零元,∧运算的单位元.

有补格

有补元的格称为有补格

a∧b = 0 和 a∨b = 1成立, 则称b是a的补元

在任何有界格中, 全下界0与全上界1互补

对于一般元素, 可能存在补元, 也可能不存在补元. 如果

存在补元, 可能是惟一的, 也可能是多个补元.

对于有界分配格, 如果元素存在补元, 一定是惟一的

子群格

没有特别懂

对一个群先找出它的所有子群

比如Z12 <0>,<1>,<2>,<3> ,<6>就是所有子群|也满足格的定义？也是子格

然后再画所有子群（子格）的Hasse图就行了

布尔代数

本质上就是一个集合

如果一个格是有补分配格, 则称

它为布尔格或布尔代数. 布尔代数标记为

<B,∧,∨,′, 0, 1>, ′为求补运算

这里面的 ' 的运算规律相当于 ‘否’

(a' )' =a 

∀a,b∈B, (a∧b)′ = a′∨b′, (a∨b) ′= a′∧b′ 

(0∧b)∨(a∧0) = 0∨0 = 0

(1∨b′)∧(a′∨1) = 1∧1 = 1

(a∧b)∧(a′∨b′) = (a∧b∧a′)∨(a∧b∧b′)

注意一下：Sn代表 n的因子所构成的集合|别到时候不知道

比如 s6={1，2，3，6}