问题：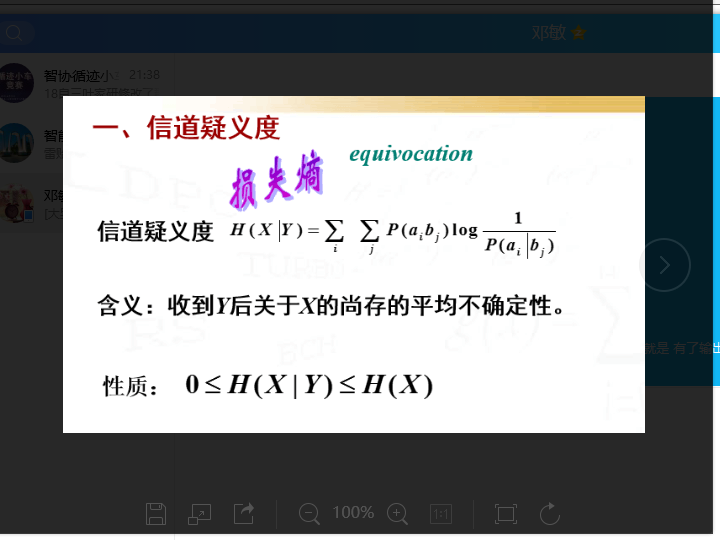
我们在讨论的时候，利用最前面的性质 ，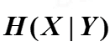
是部分信息，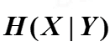
是信源熵，
可是没有关心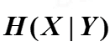 是怎么来的？？
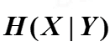
是因为有噪声系统信道传递矩阵的除开对角线以外的元素才不等于0
要是没有噪声，就压根没有引进H(X|Y)的必要。 （信道传递矩阵定义参考p75面）
有一点值得特别提出，（书上p71面）对于无干扰信道的定义，
他这里格外强调，输出信号Y和输入信号X,是确定的，一一对应，
什么是 “一一对应”？
就是我不允许你一对多，我也不允许你多对一， 一定要是双射，既是单射，又是满射。
按照一一对应的法则，求出来的无噪声信道转移概率一定可以写成 diag{p1，p2，p3.。。。pn} 的形式。
我的输出Y的个数=输入X的个数=转移矩阵的秩=n 。
以上是无噪声的讨论，
现在我加入了噪声，势必引起，信道转移矩阵除开非对角线还存在元素不为0的情况。
这也就是为什么要引入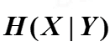是我的噪声，引起了
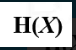变化。，我用原来
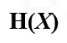信源熵的转移矩阵产生的信息量减去，我噪声
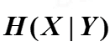
产生的信息量，得到的结果就是我输出真实的信息量
。之所以认为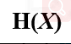
减去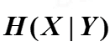
，会把真实的信息减去，错误认为Y=f（x） 会一直不变。（对角线的元素已经变了。至少变了一个）
事实上，有噪声的时候。无噪声信道输入输出的对应法则 f 已经被噪声打破
综上：
利用 矩阵运算：
输入X *(用原来满秩的转移矩阵的减取噪声产生的矩阵) =平均互信息 ，
换句话说，我信息熵减去噪声作用在信息源的熵（损失熵） 就算我真正有用的信息传输率