Chapter 2：Getting Started

 

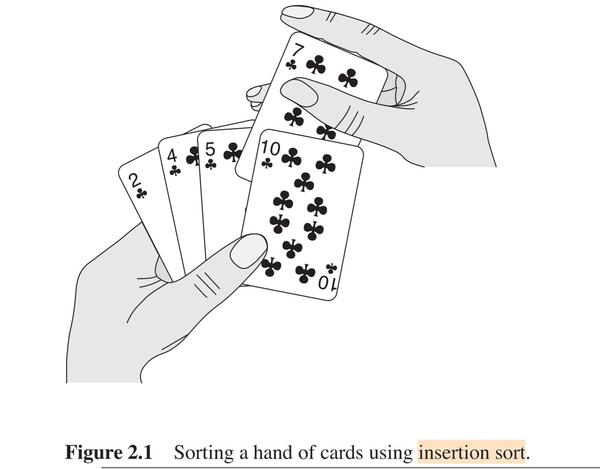
2.1 Insertion Sort

 

2.2 Analyzing algorithms

Worst-case and average-case analysis

In our analysis of insertion sort, we looked at both the best case, in which the input array was already sorted, and the worst case, in which the input array was reverse sorted. For the remainder of this book, though, we shall usually concentrate on finding only the worst-case running time, that is, the longest running time for any input of size n. We give three reasons for this orientation.

The worst-case running time of an algorithm gives us an upper bound on the running time for any input. Knowing it provides a guarantee that the algorithm will never take any longer. We need not make some educated guess about the running time and hope that it never gets much worse.

For some algorithms, the worst case occurs fairly often. For example, in searching a database for a particular piece of information, the searching algorithm’s worst case will often occur when the information is not present in the database. In some applications, searches for absent information may be frequent.

The “average case” is often roughly as bad as the worst case. Suppose that we randomly choose n numbers and apply insertion sort. How long does it take to determine where in subarray A[i.. j - 1] to insert element A[ j ]? On average, half the elements in A[1.. j - 1 ] are less than A[ j ], and half the elements are greater. On average, therefore, we check half of the subarray A[i... j - 1], and so t_{j} is about j/2. The resulting average-case running time turns out to be a quadratic function of the input size, just like the worst-case running time.

We usually consider one algorithm to be more efficient than another if its worst case running time has a lower order of growth.

 

2.3 Designing algorithms

2.3.1 The divide-and-conquer approach

Divide the problem into a number of subproblems that are smaller instances of the same problem. Conquer the subproblems by solving them recursively. If the subproblem sizes are small enough, however, just solve the subproblems in a straightforward manner. Combine the solutions to the subproblems into the solution for the original problem.

---

---

/**
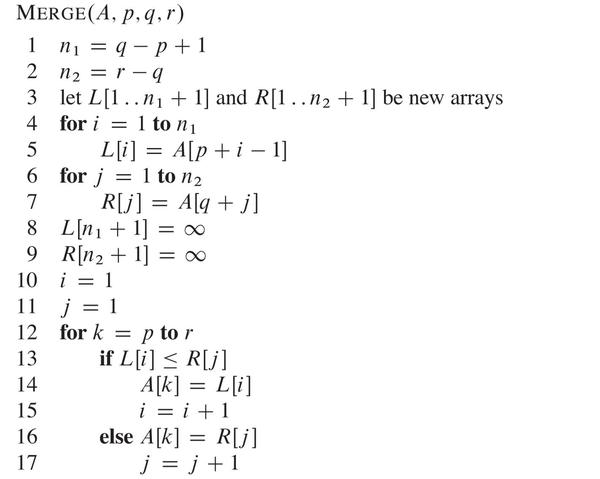
 * Describe a θ(n lg(n))-time algorithm that, given a set S of n integers
 * and another integer x, determines whether or not there exist two elements in S
 * whose sum is exactly x.
 * <p>
 * 先用merge sort排序, 再用两根指针分别在集合的头和尾,往中间扫描, 本题可用哈希表达到O(n)
 */

import java.util.HashMap;

public class TestClass {
    public static void main(String[] args) {
        int[] a = new int[100000];
        for (int i = 0; i < a.length; i++)
            a[i] = a.length - i;
        for (int i : a)
            System.out.print(a[i - 1] + " ");
        mergeSort(a, 0, a.length - 1);
        long start1 = System.currentTimeMillis();
        System.out.println(new TestClass().findIndex(a, 896));
        long end1 = System.currentTimeMillis();
        long start2 = System.currentTimeMillis();
        System.out.println(new TestClass().find(a, 896));
        long end2 = System.currentTimeMillis();
        long time1 = end1 - start1;
        long time2 = end2 - start2;
        System.out.println(time1 + "  " + time2);
    }

    static void merge(int[] a, int p, int q, int r) {
        int n1 = q - p + 1;
        int n2 = r - q;
        int[] left = new int[n1 + 1];
        int[] right = new int[n2 + 1];
        int i = 0, j = 0;
        for (i = 0; i < n1; i++) {
            left[i] = a[p + i];
        }
        for (j = 0; j < n2; j++)
            right[j] = a[q + j + 1];
        left[n1] = Integer.MAX_VALUE;
        right[n2] = Integer.MAX_VALUE;

        i = 0;
        j = 0;
        for (int k = p; k <= r; k++) {
            if (left[i] < right[j]) {
                a[k] = left[i];
                i++;
            } else {
                a[k] = right[j];
                j++;
            }
        }
    }

    static void mergeSort(int[] a, int p, int r) {
        if (p < r) {
            int q = (p + r) / 2;
            mergeSort(a, p, q);
            mergeSort(a, q + 1, r);
            merge(a, p, q, r);
        }
    }

    public HashMap<Integer, Integer> findIndex(int[] a, int sum) { // 时间复杂度为n,配合merge sort，时间复杂度为n*lg(n)。
        HashMap<Integer, Integer> elements = new HashMap<>();
        int i = 0;
        int j = a.length - 1;
        int m = a[i];
        int n = a[j];
        while (i < j) {
            if (a[i] + a[j] == sum) {
                elements.put(i, j);
            }
            if (a[i] + a[j] < sum) {
                i++;
            } else {
                j--;
            }
        }
        return elements;

    }

    public HashMap<Integer, Integer> find(int[] a, int sum) { // 笨方法，时间复杂度为n^2
        HashMap<Integer, Integer> elements = new HashMap<>();
        for (int i = 0; i < a.length - 1; i++)
            for (int j = i + 1; j < a.length; j++)
                if (a[i] + a[j] == sum)
                    elements.put(i, j);
        return elements;
    }
}