一、实验目的
通过本实验的学习理解Dijkstra算法,并且编码实现最短路径问题。
二、实验内容
本Dijkstra算法实验采用了java实现,所以解决方案也使用了java中的接口,有map映射还有set集合。
Dijkstra算法属于一种贪心算法,它使用了广度优先搜索来解决带有权值的有向图或者无向图的单源最短路径问题,该算法不能计算带有负权值的有向图或无向图,该算法的目的是求其他节点到源的最短路径。
Dijkstra算法采用的是一种贪心的策略,利用Map对象path存储每个节点名称和这个节点到相邻节点的距离,使用set集合保存已经找到了最短路径的节点的集合close,用set对象open存储未处理的节点的集合。初始时,原点 a 的路径权重被赋为 0 。同时设所有其他(a不能直接到达的)节点的路径长度MAX_VALUE。初始时,close中只有节点s。 然后,从节点a开始,遍历所有节点,选出距离a节点最短的key值,取代a节点。并把这个最短距离存到path中。然后,我们需要看看新加入的节点是否可以到达其他顶点并且看看通过该节点到达其他点的路径长度是否比a点直接到达短,如果是,那么就替换这些顶点在PATH中的值。 然后,又找下一个里节点最近的key值,重复上述动作,直到close中包含了图的所有顶点。
三、实验要求
编码实现下图中顶点A到任一顶点的最短路径:

四、实验过程
1、过程分析
首先,利用继承Map接口的HashMap类存储图中的信息,其中的key为图中的各节点的名称,value为各节点与相应节点之间连线的权值。而Map对象Path存储的是a节点到各个子节点的权值,以及该节点的名称,另一个Map对象child中存储的是各个节点到相邻节点的权值和该节点的名称,而Map对象PathInfo存储的是路径信息。
之后就是开始实现Dijkstra算法了,本代码中封装了一个Dijkstra类,包括getshortestPath,computPath,PrintPathInfo.三个方法。
顾名思义,getshortestPath方法是用来求最短路径的,他返回的是一个节点,给这个类一个实参,即节点,遍历图中依然留在open中的节点,利用之前在child中储存的权值信息,可以得到离实参这个节点最近的节点。其中的关键过程就是比较现在的distance和minDis,如果distance小,就会被赋值给minDis,随着遍历的进行,minDis不断被赋值,遍历结束后,minDis的值就是最短距离,而相对应的key值,就是离实参这个节点最近的子节点。
computPath方法是用来计算节点之间的距离的,该方法的关键过程就是首先利用上面的getshortestPath方法获取离上一个源点最近的子节点nearst,然后在该节点的基础上,求open中的节点到a点的路径newCompute,如果newCompute这个值小于Path中储存的该open中的节点到a节点的距离,那么就用这个newCompute替换Path中的值,同时更新PathInfo的值。其中newCompute的求法是拿Path中nearst节点对应的权值加上child中该open中的节点到nearst的权值。该类通过递归实现Path中的value不断被更小的值赋值,从而得到最终的最短路径。
PrintPathInfo方法是用来打印路径信息的,打印的是PathInfo中的键值。
2、实验结果
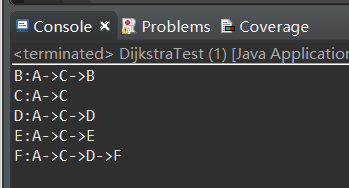
五、实验总结
关于Dijkstra算法,刚开始做的时候遇到了较大的阻力,为了更好的理解这个算法的思想,我们从网上找了四五个关于这个算法的例子,不断地模拟解决过程,最终得到了Dijkstra算法的精髓,明白了关于其中的过程。这个过程花了很长时间,之后就是用代码实现了,因为该算法涉及键值对,恰好java语言中有Map接口,所以我们就选择了java作为基础语言去实现这个Dijkstra算法,其中也是历经了千辛万苦,所幸的是,java中关于set集合,和Map接口的子类以及他们的方法让我们更加熟悉,通过这次实验我们不仅进一步的学习了java,也掌握了一门算法,总之,过程是苦的,但是结果很快乐。
感谢教授本实验的老师,让我们获取了这样一个吸收知识的机会,只是我们自身有很多只是漏洞,需要进一步的学习。
附录(源代码)
package cn.sal.lisan;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;
import cn.sal.Lisan2.MapBuilder;
import cn.sal.Lisan2.Node;
class Node {
private String name;
private Map<Node,Integer> child=new HashMap<>();
public Node(String name){
this.name=name;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Map<Node, Integer> getChild() {
return child;
}
public void setChild(Map<Node, Integer> child) {
this.child = child;
}
}
class MapBuilder {
public Node build(Set<Node> open, Set<Node> close){
Node nodeA=new Node("A");
Node nodeB=new Node("B");
Node nodeC=new Node("C");
Node nodeD=new Node("D");
Node nodeE=new Node("E");
Node nodeF=new Node("F");
//使用node类里的getchild()方法,再利用散列映射的put方法,将其他节点和权值关联后添加进去
nodeA.getChild().put(nodeB, 6);
nodeA.getChild().put(nodeC, 3);
nodeB.getChild().put(nodeA, 6);
nodeB.getChild().put(nodeC, 2);
nodeB.getChild().put(nodeD, 5);
nodeC.getChild().put(nodeA, 3);
nodeC.getChild().put(nodeB, 2);
nodeC.getChild().put(nodeD, 3);
nodeC.getChild().put(nodeE, 4);
nodeD.getChild().put(nodeB, 5);
nodeD.getChild().put(nodeC, 3);
nodeD.getChild().put(nodeF, 3);
nodeD.getChild().put(nodeE, 2);
nodeE.getChild().put(nodeC, 4);
nodeE.getChild().put(nodeD, 2);
nodeE.getChild().put(nodeF, 5);
nodeF.getChild().put(nodeD, 3);
nodeF.getChild().put(nodeE, 5);
open.add(nodeB);
open.add(nodeC);
open.add(nodeD);
open.add(nodeE);
open.add(nodeF);
close.add(nodeA);
return nodeA;
}
}
class Dijkstra {
Set<Node> open = new HashSet<Node>();
Set<Node> close = new HashSet<Node>();
Map<String, Integer> path = new HashMap<String, Integer>();//封装路径距离
Map<String, String> pathInfo = new HashMap<String, String>();//封装路径信息
public Node init() {
//初始路径,因没有A->E这条路径,所以path(E)设置为Integer.MAX_VALUE
path.put("B", 6);
pathInfo.put("B", "A->B");
path.put("C", 3);
pathInfo.put("C", "A->C");
path.put("D", Integer.MAX_VALUE);
pathInfo.put("D", "A->D");
path.put("E", Integer.MAX_VALUE);
pathInfo.put("E", "A");
path.put("F", Integer.MAX_VALUE);
pathInfo.put("F", "A->F");
//将初始节点放入close,其他节点放入open
Node start = new MapBuilder().build(open, close);
return start;
}
/**
* 获取与node最近的子节点
*/
private Node getShortestPath(Node node) {
Node res = null;
int minDis = Integer.MAX_VALUE;
Map<Node, Integer> childs = node.getChild();
// 遍历与Node相连接的所有节点,选取其中距离最短的节点
for (Node child : childs.keySet()) {//keyset()方法用来返回键即节点
if (open.contains(child)) {
int distance = childs.get(child);
if (distance < minDis) {
minDis = distance;
res = child;
}
}
}
return res;
}
/*
* 计算路径
*
*
*
*/
public void computePath(Node start) {
//取距离start节点最近的子节点,放入close
Node nearest = getShortestPath(start);
if (nearest == null) {
return;
}
close.add(nearest); //已遍历的
open.remove(nearest); //未遍历的
Map<Node, Integer> childs = nearest.getChild();//getChild()返回child 对象,
//child中存储了各节点到相邻节点的距离·
for (Node child : childs.keySet()) {//遍历最近的节点
if (open.contains(child)) {//如果子节点在open中
Integer newCompute = path.get(nearest.getName()) + childs.get(child);
//Map接口的get()方法用来返回key所对应的value,
//此句是用来计算neareset这个节点到每个子节点的距离
if (newCompute < path.get(child.getName())) {
//新计算出来的距离小于之前设置的距离
path.put(child.getName(), newCompute);
pathInfo.put(child.getName(), pathInfo.get(nearest.getName()) + "->" + child.getName());
}
//本if语句可以用来更新A到子节点的最短距离
}
}
computePath(start);//重复执行自己,确保所有子节点被遍历
computePath(nearest);//向外一层层递归,直至所有顶点被遍历
}
public void printPathInfo() {
//entrySet()返回此映射中包含的映射关系的set视图
Set<Map.Entry<String, String>> pathInfos = pathInfo.entrySet();
for (Map.Entry<String, String> pathInfo : pathInfos) {
System.out.println(pathInfo.getKey() + ":" + pathInfo.getValue());
}
}
}
public class DijkstraTest {
public static void main(String args[]) throws Exception {
Dijkstra test=new Dijkstra();
Node start=test.init();
test.computePath(start);
test.printPathInfo();
}
}