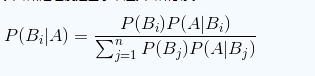一.学习笔记
1概率论与贝叶斯先验
(1)本福特定律

(2)概率公式

(3)贝叶斯公式

(4)贝叶斯公式的运用

(5)两点分布

(6)二项分布法一:

(7)二项分布法二:
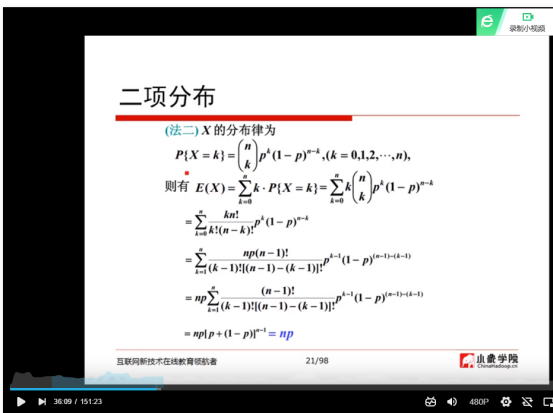
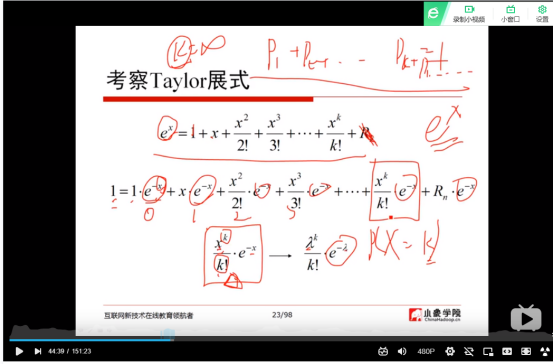
(8)泰勒展式:
(9)泊松分布


(10)均匀分布

(11)指数分布


(12)指数分布的无记忆性

(13)正态分布

正态分布的期望

正态分布的方差

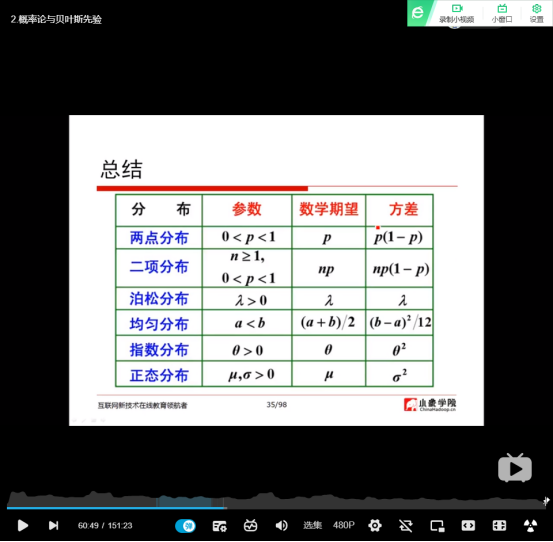
(14)常见分布的期望与方差总结
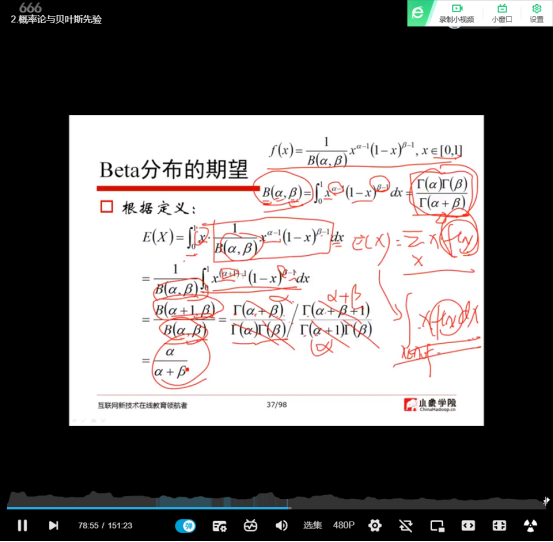
(15)Beta分布

Beta分布的期望
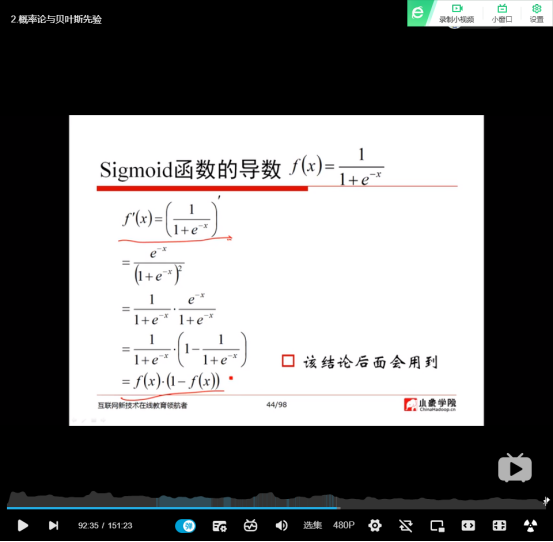
(16)Sigmoid函数的导数
(17)高斯分布也属于指数族

(18)事件的独立性

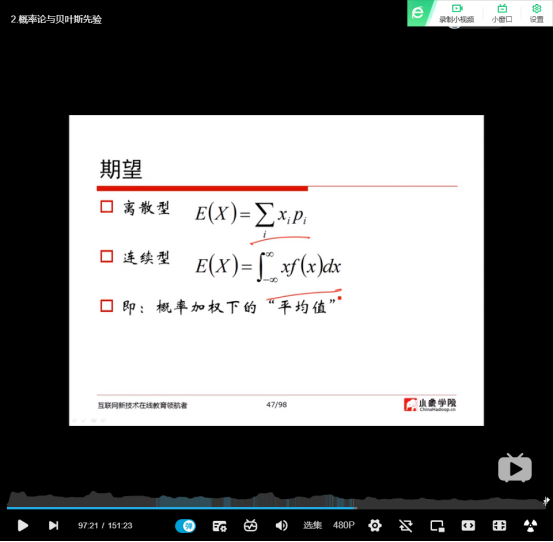
(19)离散与连续型的期望
(20)期望的性质:

(21)相同取0,不同取1

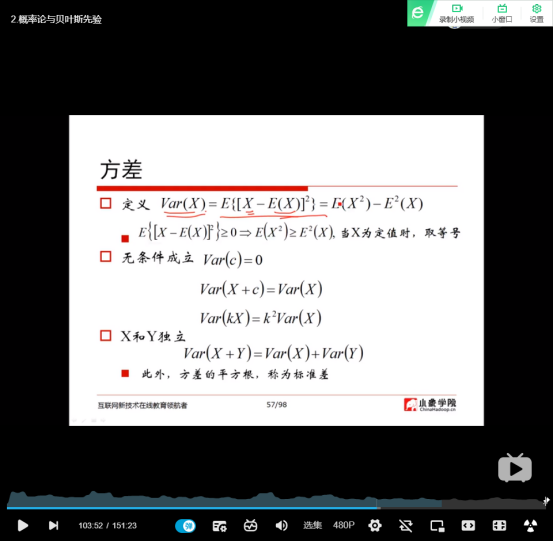
(22)方差(方差的平方根为标准差)
(23)协方差(协作在一起所形成的方差)
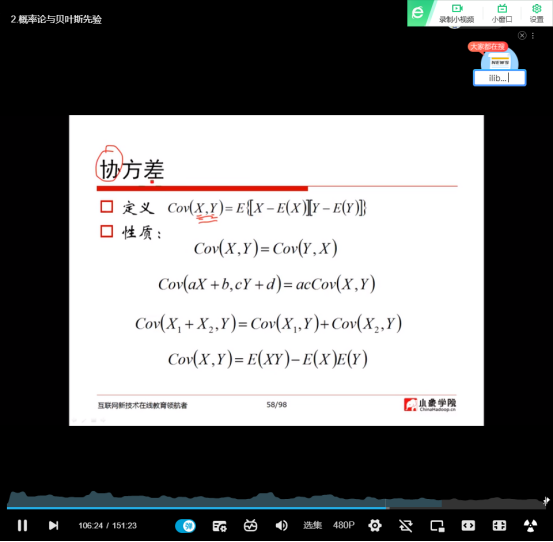
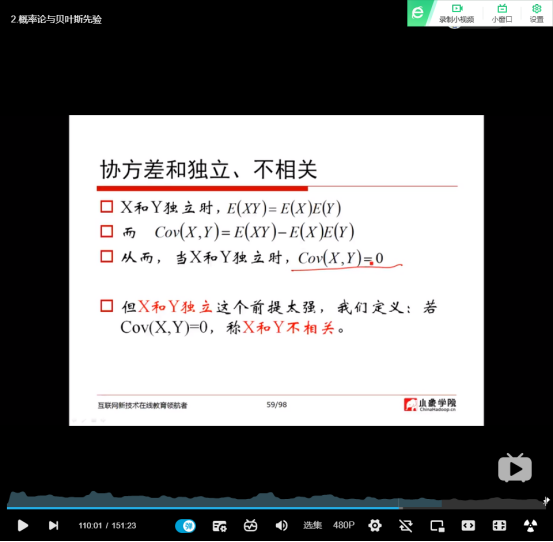
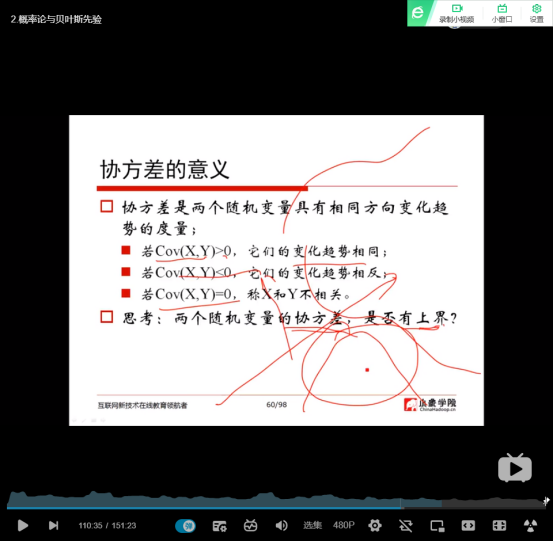
(24)person相关系数

(25)协方差矩阵

(26)切比雪夫不等式

(27)大数定律

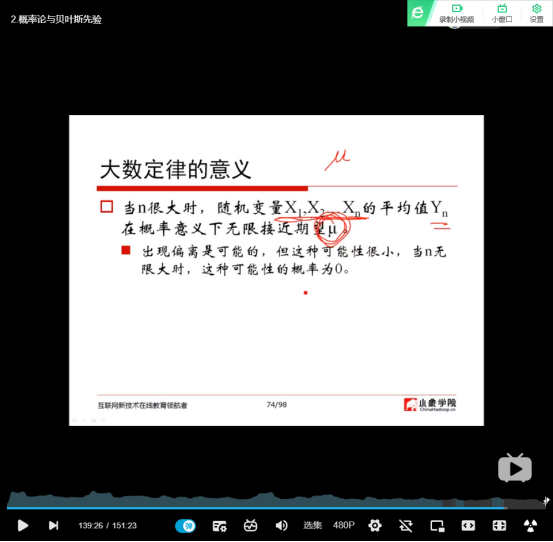
(28)伯努利定理

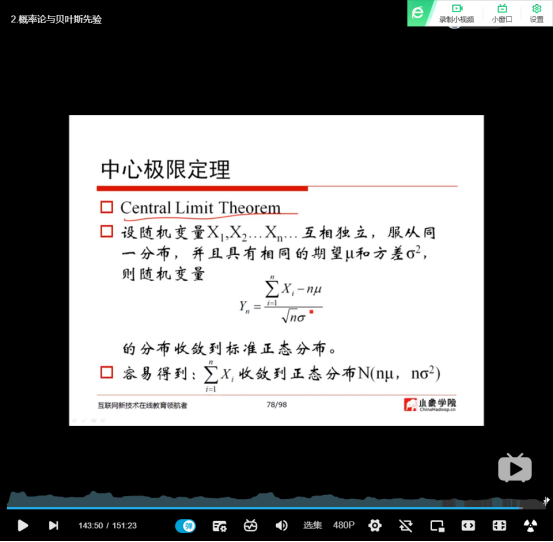
(29)中心极限定理
2.矩阵和线性代数
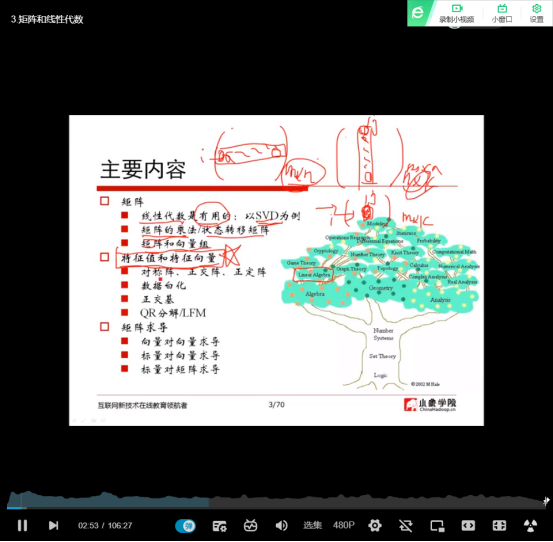
(1)主要内容
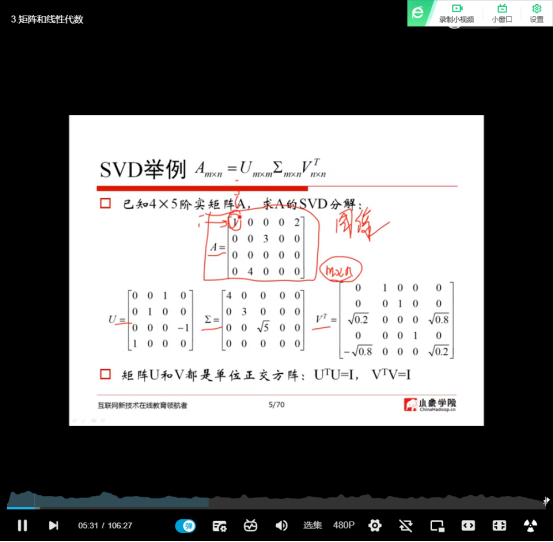
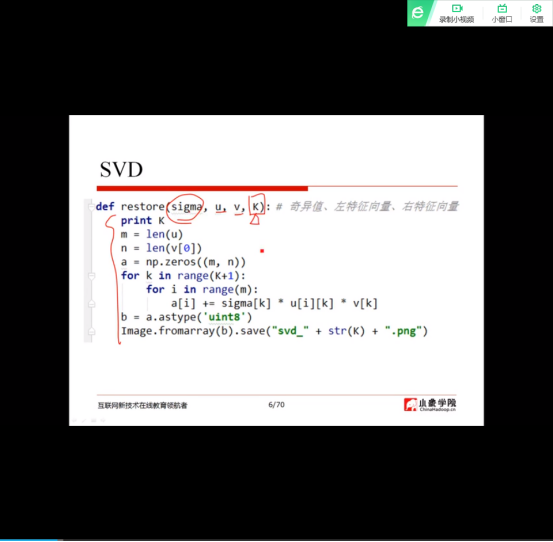
(2)SVD

(3)线性代数
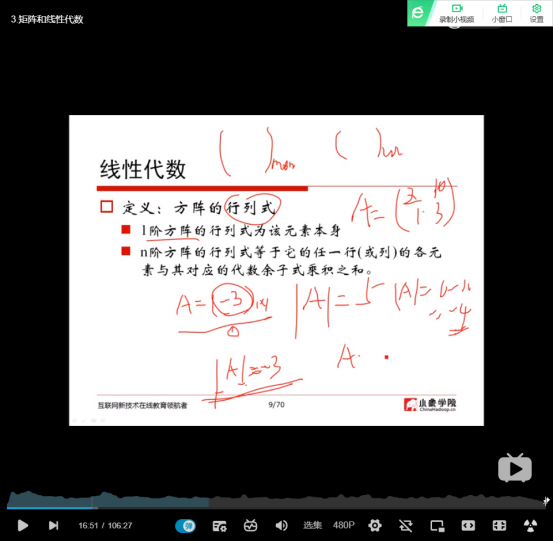
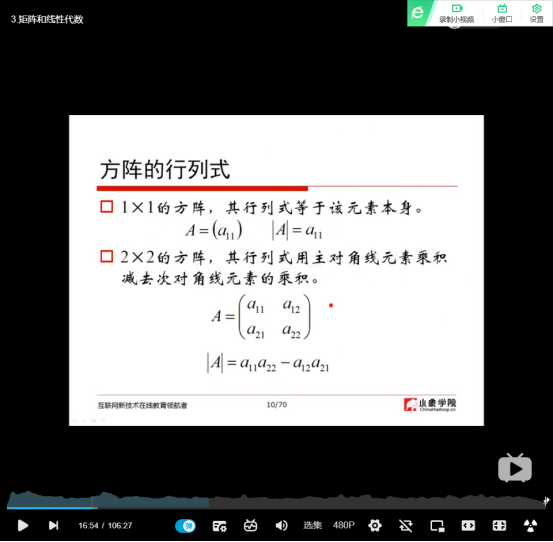
(4)方阵的行列式
(5)代数余子式

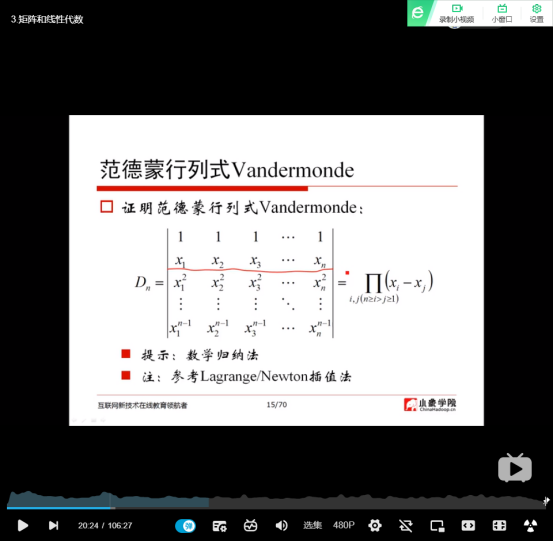
(6)范德蒙行列式
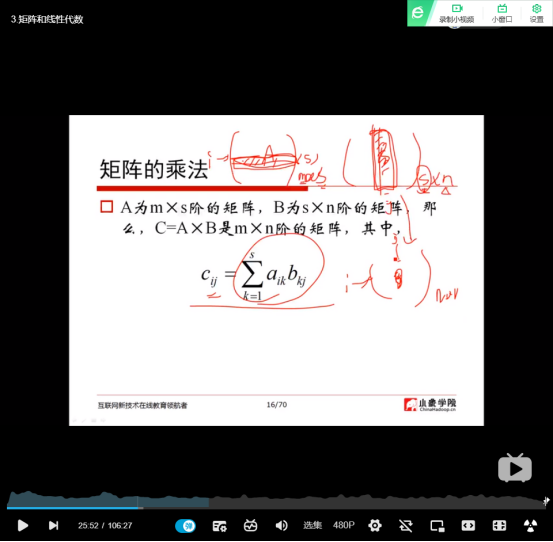
(7)矩阵的乘法

(8)方阵的行列式

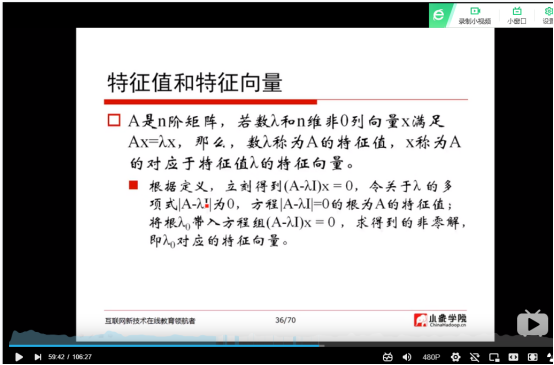
(9)特征值和特征向量
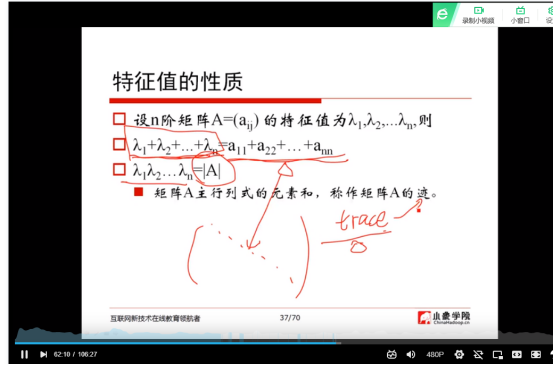
(10)特征值的性质
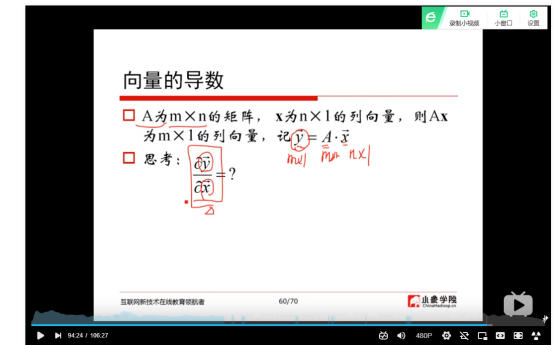
(11)向量的导数
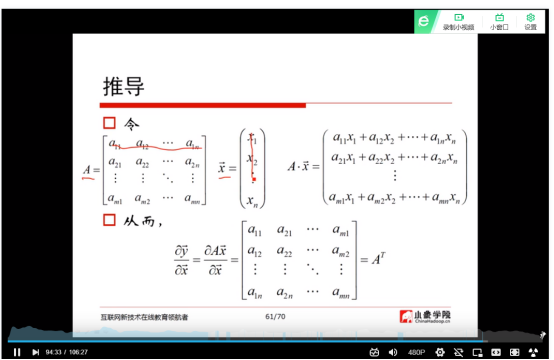
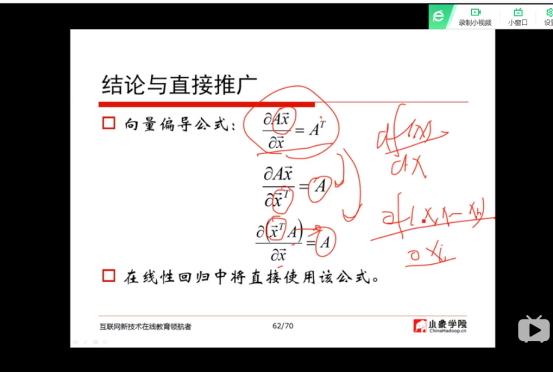
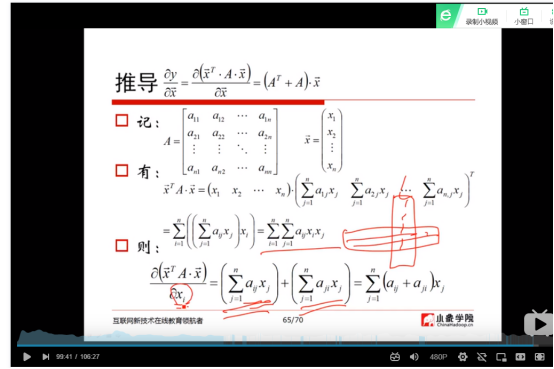
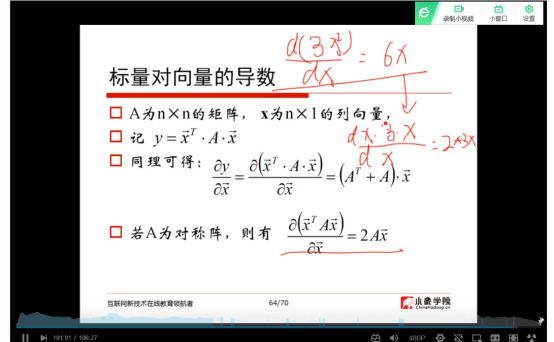
(12)标量对向量的导数
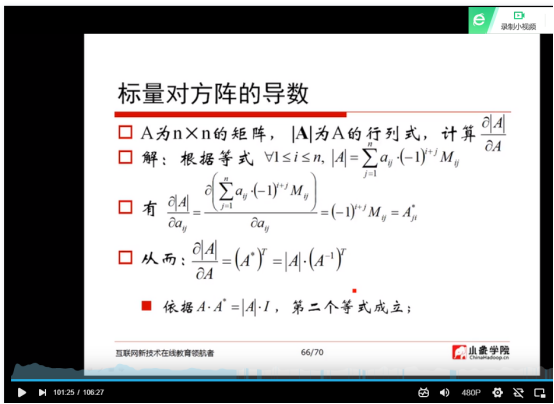
(13)标量对方阵的导数
二、用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”。
1.梯度:
首先梯度是一个是一个矢量,有大小和方向,在这一点上沿着方向的方向导数的函数的最大值,也就是函数在该点的可以取到的最大导数称作梯度。
2.梯度下降:
就是如何能最快下山的过程,梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这就是梯度下降所要得到的,最快下山的方向。
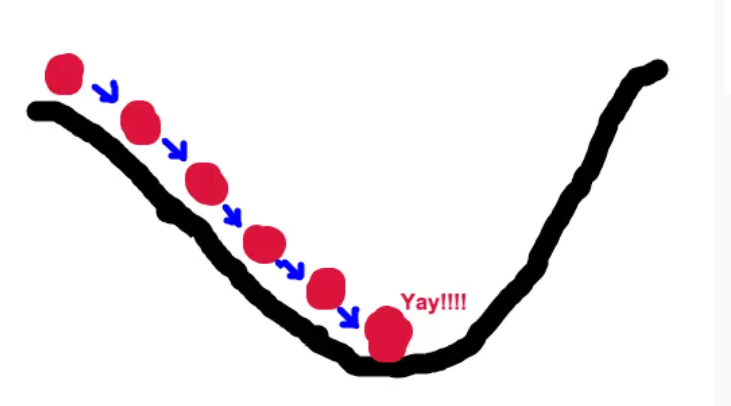
3.贝叶斯定理:
在使用概率对某一件事情进行推断之前,我们已经得到了关于这一事件的概率,这种概率称为先验概率,但是通过后续的研究采集后又获得了有关该事件的概率,我们就可以对先验概率进行调整,然后先验概率就变为后验概率,这个修正概率的定理就是贝叶斯定理,我们可以利用他来求得,已知某一事件发生的概率,求得另一事件一起发生的概率,公式如下: