梯度消失(Vanishing Gradient Problem)
-
定义
1980年代常用的激活函数是sigmoid函数。以MNIST手写数字识别为例,在使用sigmoid函数时会发现随着神经网络层数增加,识别准确率逐渐下降,这个现象的原因并不是过拟合(原因见上文),而是梯度消失。
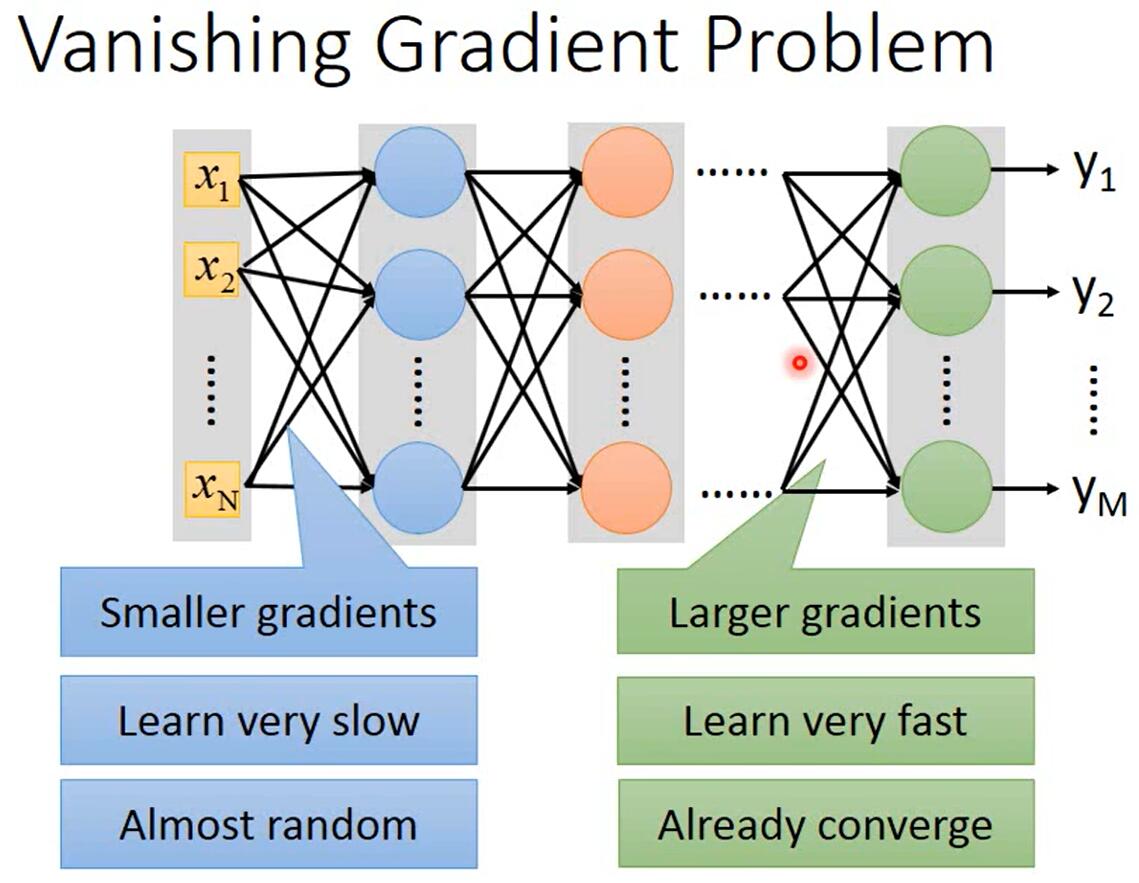
如上图所示,当神经网络层数很多时,靠近输入层的参数的梯度会很小,靠近输出层的参数的梯度会很大。当每个参数的学习率相同时,靠近输入层的参数会更新得很慢,靠近输出层的几层参数会更新得很快。所以,当靠近输入层的参数几乎还是随机数时,靠近输出层的参数已经收敛了。
-
原因
按照反向传播的式子,这确实是会发生的。
直观感觉上,sigmoid函数输入的范围是无穷大,但输出的范围是[0,1],也就是说sigmoid函数减弱了输入变化导致输出变化的幅度。那为什么靠近输出层的参数的梯度更大呢?sigmoid函数是一层层叠起来的,不断地减弱靠近输入层的参数的变化导致输出变化的幅度,所以更靠后的参数的梯度越大。
-
解决方法
Hinton提出无监督逐层训练方法以解决这个问题,其基本思想是每次训练一层隐节点。
后来Hinton等人提出修改激活函数,比如换成ReLU。
ReLU(Rectified Linear Unit)
-
定义
当输入小于等于0时,输出为0;当输入大于0时,输出等于输入。
-
优点
相比于sigmoid函数,它有以下优点
- 运算更快
- 更符合生物学
- 等同于无穷多个bias不同的sigmoid函数叠加起来
- 可以解决梯度消失问题
-
如何解决梯度消失问题
当ReLU输出为0时该激活函数对神经网络不起作用,所以在神经网络中生效的激活函数都是输出等于输入,所以就不会出现sigmoid函数导致的减弱输入变化导致输出变化的幅度的情况。
-
ReLU会使整个神经网络变成线性的吗?
可知有效的激活函数都是线性的,但整个神经网络还是非线性的。当输入改变很小、不改变每个激活函数的Operation Region(操作区域,大概意思就是输入范围)时,整个神经网络是线性的;当输入改变很大、改变了Operation Region时,整个神经网络就是非线性的。目前我是凭直觉理解这一点,还未细究
-
ReLU可以做微分吗?
不用处理输入为0的情况,当输入小于0时,微分就是0,当输入大于0时微分就是1。
Leaky ReLU
当输入小于等于0时,输出为输入的0.01倍;当输入大于0时,输出等于输入。
Parametric ReLU
当输入小于等于0时,输出为输入的(alpha)倍;当输入大于0时,输出等于输入。
其中(alpha)是通过梯度下降学习到的参数
Maxout
-
定义
通过学习得到一个激活函数,人为将每层输出的多个值分组,然后输出每组值中的最大值。(跟maxpooling一模一样)
-
ReLU是Maxout的一个特例
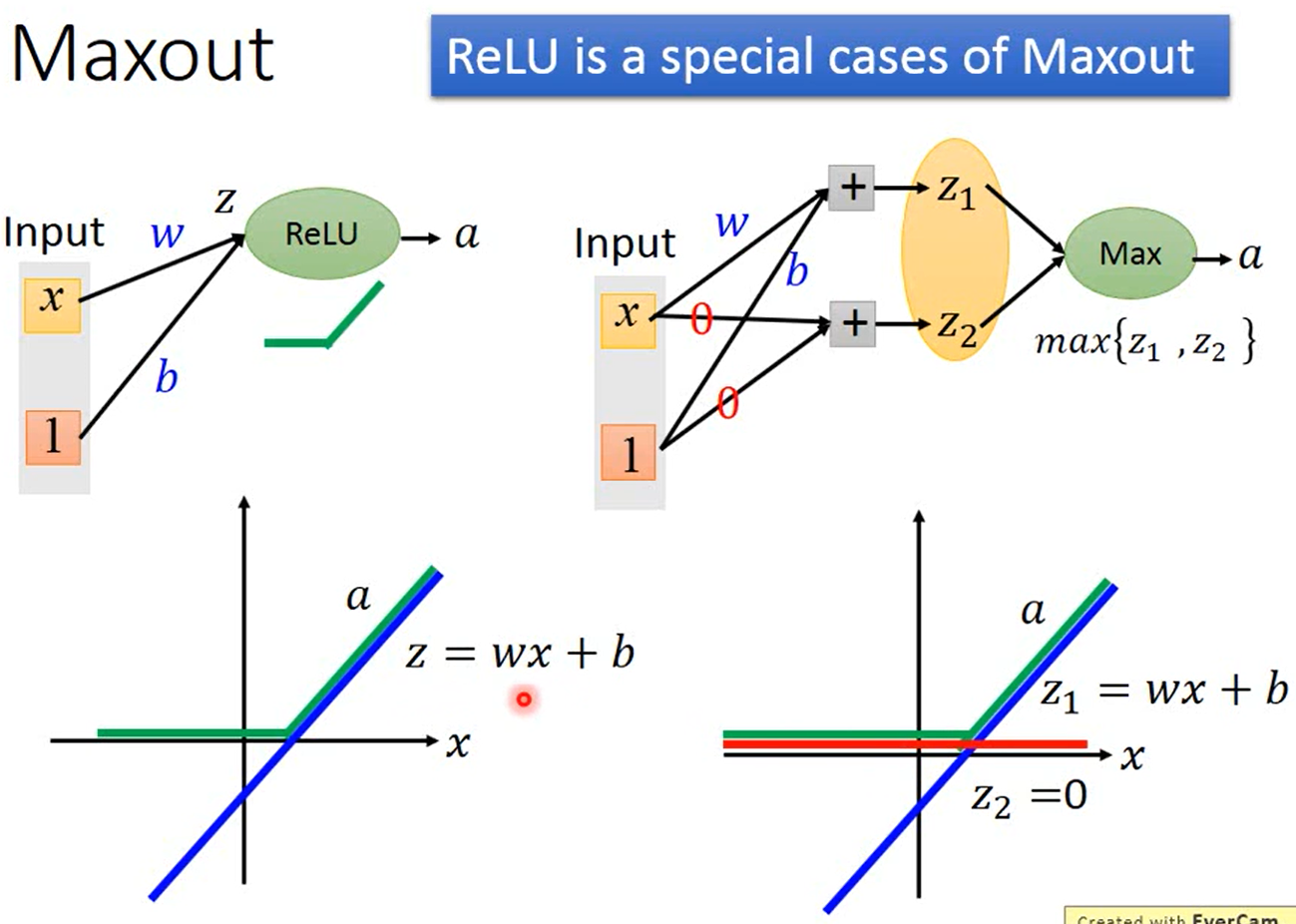
-
Maxout比ReLU包含了更多的函数
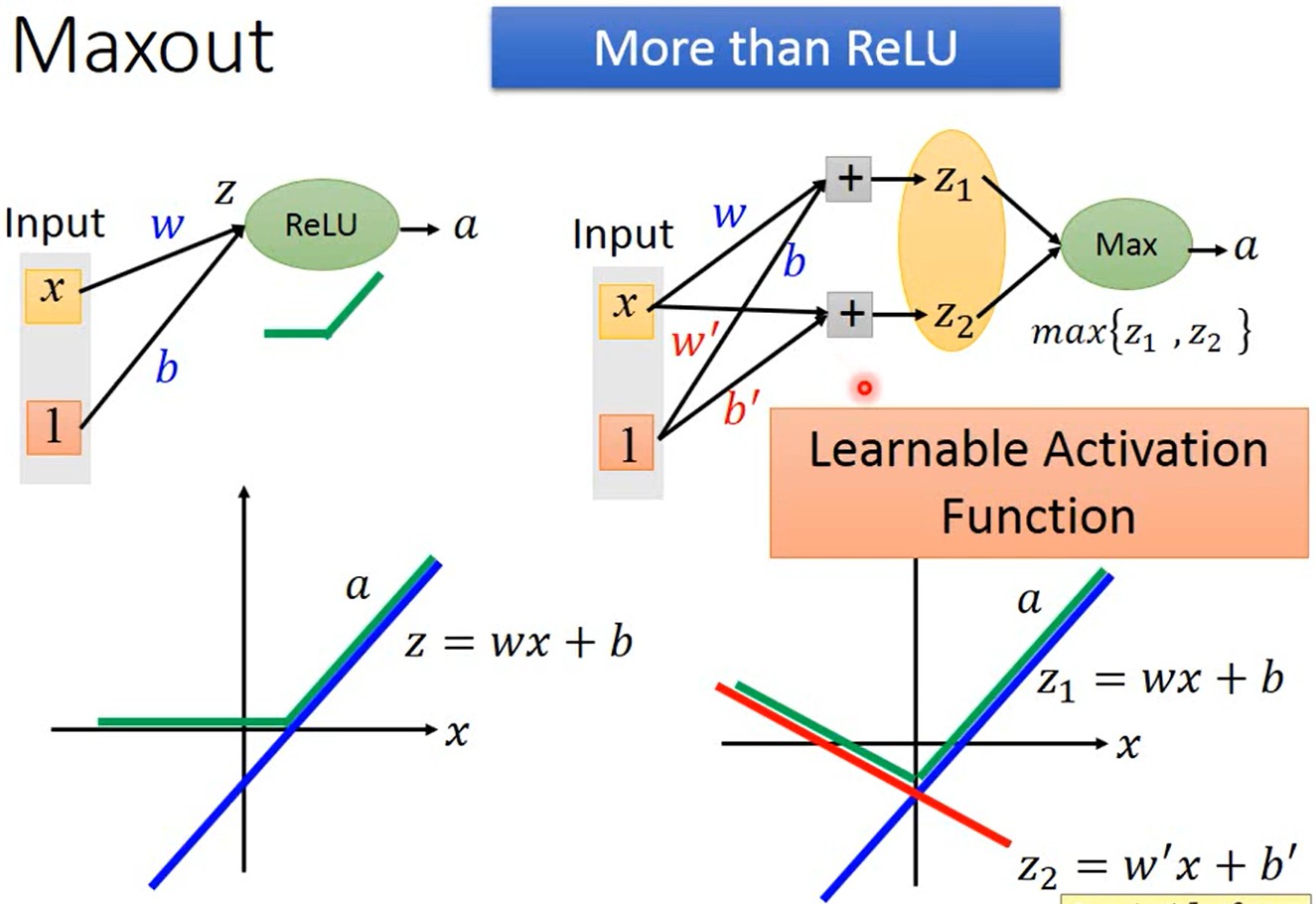
-
Maxout可以得到任意的分段线性凸函数(piecewise linear convex),有几个分段取决于每组里有几个值
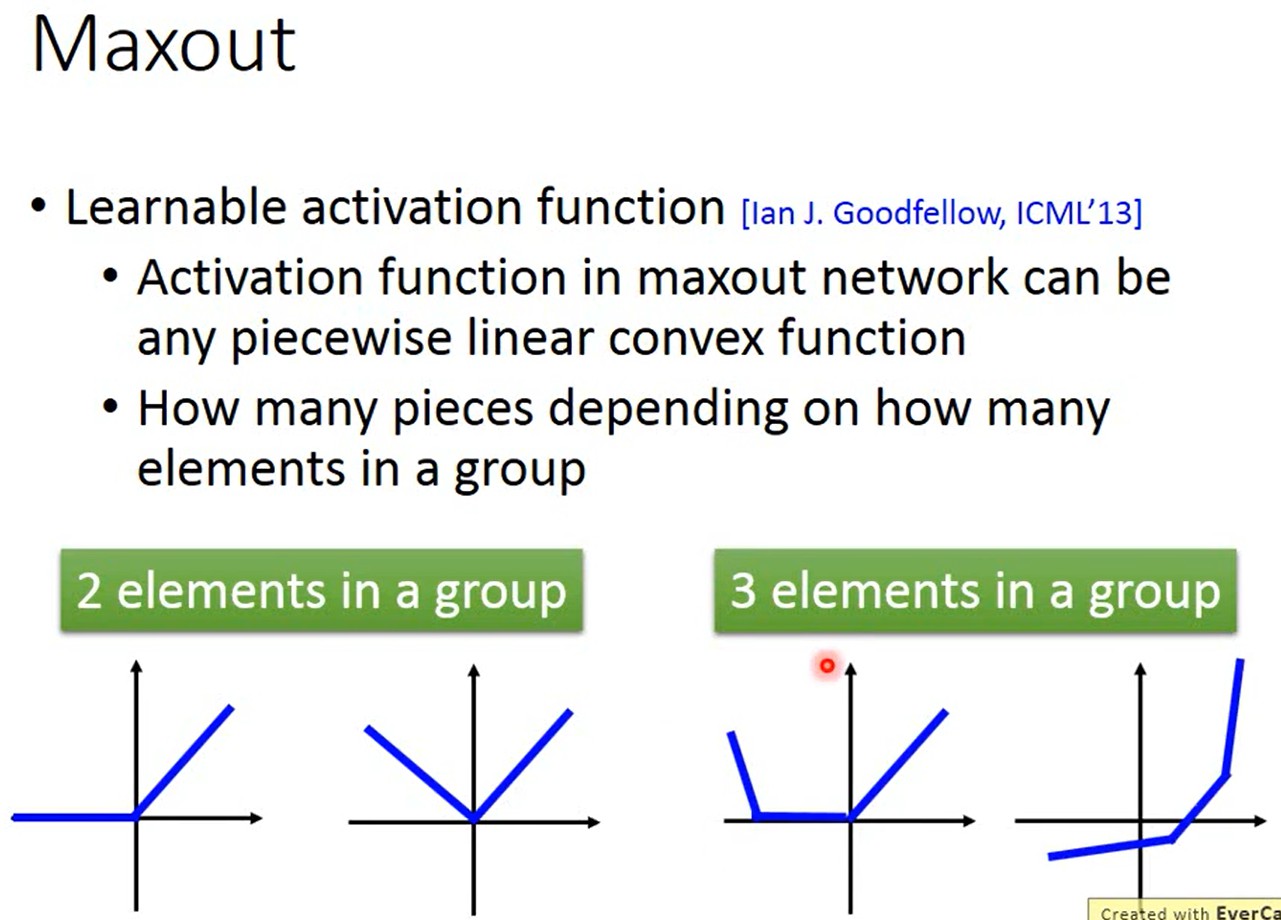
-
如何训练Maxout
Maxout只是选择输出哪一个线性函数的值而已,因此Maxout激活函数还是线性的。
因为在多个值中只选择最大值进行输出,所以会形成一个比较瘦长/窄深的神经网络。
在多个值中只选择最大值进行输出,这并不会导致一些参数无法被训练:因为输入不同导致一组值中的最大值不同,所以各个参数都可能被训练到。
当输入不同时,形成的也是不同结构的神经网络。
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!