Day1
这套题还可以,但是由于重大失误,只拿到了140.
T1
【问题描述】
给你一个字符串,字符串中若有连续的2个字符相同,则可以将这两个字符消去。求消去之后的字符串。
【题解】
这题送分的。。。
据说正解是用栈来写,但是我用模拟链表的方法搞了搞,结果比标程跑的还快。。。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<cmath> 6 #include<ctime> 7 #include<algorithm> 8 using namespace std; 9 #define FILE "string" 10 #define MAXN 200010 11 char ch[MAXN]; 12 int n,last[MAXN],vis[MAXN]; 13 int main() 14 { 15 freopen(FILE".in","r",stdin); 16 freopen(FILE".out","w",stdout); 17 scanf("%s",ch+1); n=strlen(ch+1); 18 for(int i=2;i<=n;i++) last[i]=i-1; 19 for(int i=1;i<=n;i++) 20 if(ch[i]==ch[last[i]]) 21 { 22 vis[i]=1;vis[last[i]]=1; 23 last[i+1]=last[last[i]]; 24 } 25 for(int i=1;i<=n;i++) if(!vis[i]) printf("%c",ch[i]); 26 printf(" "); 27 return 0; 28 }
T2
【问题描述】
有两个整数x,y,初始时x=y=1,给定一个数z和两种操作:
X操作:x=x+y
Y操作:y=x+y
你的目标是在最少的运算次数下,让X=Z,Y随意。
你需要输出运算序列(一次X操作表示为X,Y同理),并让这个运算序列的字典序最小。
【题解】
我们发现正着搜索时间复杂度太高,而末状态的x值是确定的,于是我们可以倒着模拟这个过程,然后。。。这道题就解决了
考试时没有排字典序,结果全部wa掉了。。。心痛啊
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<ctime> 6 #include<cmath> 7 #include<algorithm> 8 using namespace std; 9 #define FILE "plus" 10 int n,len,minn(1000000000); 11 char q[1000010],ans[1000010]; 12 inline int read() 13 { 14 int x=0,f=1; char ch=getchar(); 15 while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} 16 while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();} 17 return x*f; 18 } 19 int dfs(int x,int y) 20 { 21 if(x<=0||y<=0) return 0; 22 if(x==1&&y==1) return 1; 23 if(x==y) return 0; 24 if(x>y) {q[++len]='X'; return dfs(x-y,y);} 25 if(x<y) {q[++len]='Y'; return dfs(x,y-x);} 26 } 27 bool check() 28 { 29 for(int i=minn;i;i--) 30 { 31 if(q[i]>ans[i]) return 0; 32 if(q[i]<ans[i]) return 1; 33 } 34 return 0; 35 } 36 int main() 37 { 38 freopen(FILE".in","r",stdin); 39 freopen(FILE".out","w",stdout); 40 int __size__=20<<20;//20MB 41 char *__p__=(char*)malloc(__size__)+__size__; 42 __asm__("movl %0, %%esp "::"r"(__p__)); 43 n=read(); 44 for(int i=n-1;i>=1;i--) 45 { 46 if(dfs(n,i)) 47 { 48 if(len<minn) 49 { 50 minn=len; 51 for(int j=1;j<=len;j++) ans[j]=q[j]; 52 } 53 if(len==minn&&check()) for(int j=1;j<=len;j++) ans[j]=q[j]; 54 } 55 len=0; 56 } 57 for(int i=minn;i;i--) printf("%c",ans[i]); 58 printf(" "); 59 return 0; 60 }
T3
这题太过毒瘤,只拿了40分的暴力。。。
关于正解先留个坑。。。(flag已立)
Day2
这套题有点狠。。。
只能拿下了暴力的110分,而Cydiater大神A掉了T1和T2,拿到了240分。sro_Cydiater_orz
T1
【问题描述】
现在有一个数列,最初包含0个数。现在要对数列操作n次,操作有3类。
1) a k,在数列的最后插入一个整数k
2) s 将最近插入的数删除。
3) t k 将数列恢复第k次操作前的状态
每次输出数列最后一个数的值,如果数列为空,输出-1。
【题解】
T1就搞了一个可持久化栈,excited
其实这个可持久化栈就是一颗树,删除就相当于返回父节点,然后注意保留历史版本就行了。
代码量很短。
1 #include<iostream> 2 #include<cstdlib> 3 #include<cstdio> 4 #include<cstring> 5 #include<ctime> 6 #include<cmath> 7 #include<algorithm> 8 using namespace std; 9 #define FILE "array" 10 #define MAXN 80010 11 typedef long long ll; 12 ll n,node,a[MAXN],fa[MAXN]; 13 inline ll read(){ 14 ll x=0,f=1; char ch=getchar(); 15 while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} 16 while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();} 17 return x*f; 18 } 19 int main(){ 20 freopen(FILE".in","r",stdin); 21 freopen(FILE".out","w",stdout); 22 n=read(); a[0]=-1; 23 for(ll i=1;i<=n;i++){ 24 char ch; scanf("%c ",&ch); 25 if(ch=='a') {ll v=read(); a[i]=v; fa[i]=node; node=i;} 26 else if(ch=='s') {node=fa[node]; a[i]=a[node]; fa[i]=fa[node]; node=i;} 27 else {ll v=read(); node=v-1; a[i]=a[node]; fa[i]=fa[node]; node=i;} 28 } 29 for(ll i=1;i<=n;i++) printf("%lld ",a[i]); 30 return 0; 31 }
T2
【问题描述】
给定n*m的地图,问图中有多少对点的gcd为1,且这两个点的距离在[l,r]内。
【题解】
如果横幅长度可以=1,那么水平和垂直都可以拉。
斜着拉横幅的情况:穷举所有的点,如果点a的坐标是(x,y),如果(x,y)到(0,0)的距离在允许范围,并且x和y的最大公约数是1的话,那么可以拉的横幅有(W-x+1)*(H-y+1)个。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<cmath> 6 #include<ctime> 7 #include<algorithm> 8 using namespace std; 9 #define FILE "blossom" 10 int n,m,l,r; 11 long long ans; 12 int gcd(int a,int b) {return !b?a:gcd(b,a%b);} 13 inline int read(){ 14 int x=0,f=1; char ch=getchar(); 15 while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} 16 while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();} 17 return x*f; 18 } 19 bool check(int x,int y){ 20 if(gcd(x,y)!=1) return 0; 21 int v=x*x+y*y; 22 if(v>=l*l&&v<=r*r) return 1; 23 return 0; 24 } 25 int main(){ 26 freopen(FILE".in","r",stdin); 27 freopen(FILE".out","w",stdout); 28 n=read(); m=read(); l=read(); r=read(); 29 for(int i=1;i<=n;i++) 30 for(int j=1;j<=m;j++) 31 if(check(i,j)) ans+=(n-i+1)*(m-j+1)*2; 32 if(l<=1) ans+=(n+1)*m+(m+1)*n; 33 printf("%lld ",ans); 34 return 0; 35 }
T3
【问题描述】
给定一个长度为n的序列,每使序列中的一个数x变为y,需要花费|x-y|的代价。问将此序列通过改变元素的值变为不下降序列,最小花费的代价。
【题解】
这题挺毒瘤的。。。
各种暴力就不说了,直接说正解。
我们用a[i]表示这个序列,设f[i][j]表示前i个数组成不下降序列且a[i]<=j的最小代价。
我们把f[i][j]看成关于j的函数,那么可以得到n条函数图像。(如下图所示)
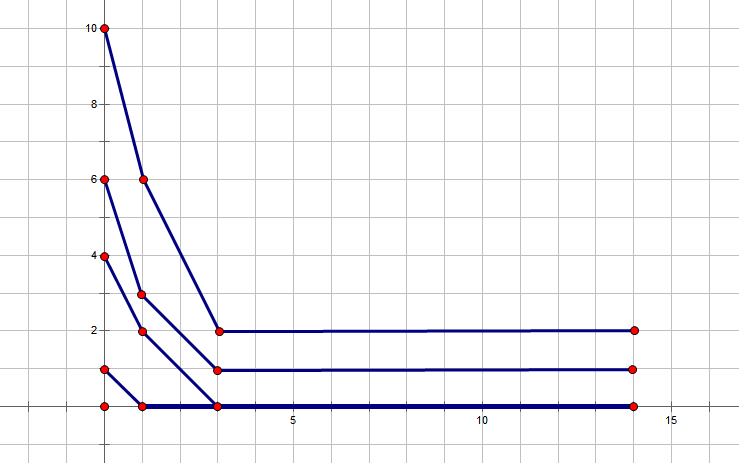
然后我们发现了一个规律,当i+1的图像和i的图像是有关系的,在a[i]之前i+1的图像的斜率是i的斜率加1
这样我们就可以用线段树维护这些线的斜率,最后的答案就是i这条线的最低点。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<ctime> 6 #include<cmath> 7 #include<algorithm> 8 using namespace std; 9 #define FILE "chen" 10 #define up(i,j,n) for(int i=j;i<=n;i++) 11 typedef long long ll; 12 const int MAXN=1e6+5; 13 const int oo=0x3f3f3f3f; 14 struct node{ll delta,v,maxx;}tr[MAXN<<2]; 15 ll n,top,ans,a[MAXN],num[MAXN],Num[MAXN],K[MAXN]; 16 namespace INIT{ 17 char buf[1<<15],*fs,*ft; 18 inline char getc() {return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;} 19 inline int read(){ 20 int x=0,f=1; char ch=getc(); 21 while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getc();} 22 while(isdigit(ch)) {x=x*10+ch-'0'; ch=getc();} 23 return x*f; 24 } 25 }using namespace INIT; 26 namespace Segment_Tree{ 27 void pushdown(int p){ 28 int delta=tr[p].delta; tr[p].delta=0; 29 if(delta==0) return; 30 tr[p<<1].maxx+=delta; tr[p<<1|1].maxx+=delta; 31 tr[p<<1].v+=delta; tr[p<<1|1].v+=delta; 32 tr[p<<1].delta+=delta; tr[p<<1|1].delta+=delta; 33 } 34 void relord(int p){ 35 tr[p].v=min(tr[p<<1].v,tr[p<<1|1].v); 36 tr[p].maxx=max(tr[p<<1].maxx,tr[p<<1|1].maxx); 37 } 38 int get(int p,int l,int r){ 39 if(l!=r) pushdown(p); 40 if(tr[p].maxx==0) return l; 41 if(l==r&&tr[p].v==0) return l; 42 if(tr[p].v>0) return oo; 43 int mid=(l+r)>>1; 44 return min(get(p<<1,l,mid),get(p<<1|1,mid+1,r)); 45 } 46 void updata(int p,int l,int r,int x,int y,int v){ 47 if(l!=r) pushdown(p); 48 if(x>r||y<l) return; 49 if(x<=l&&y>=r){tr[p].maxx+=v; tr[p].v+=v; tr[p].delta+=v; return;} 50 int mid=(l+r)>>1; 51 updata(p<<1,l,mid,x,y,v); 52 updata(p<<1|1,mid+1,r,x,y,v); 53 relord(p); 54 } 55 void res(int p,int l,int r){ 56 if(l==r){K[l]=tr[p].v; return;} 57 pushdown(p); 58 int mid=(l+r)>>1; 59 res(p<<1,l,mid); 60 res(p<<1|1,mid+1,r); 61 relord(p); 62 } 63 }using namespace Segment_Tree; 64 int find(int x){ 65 int l=1,r=top; 66 while(l+1<r){ 67 int mid=(l+r)>>1; 68 if(num[mid]>x) r=mid; 69 else l=mid; 70 } 71 if(num[l]==x) return l; 72 else return r; 73 } 74 void init(){ 75 n=read(); 76 up(i,1,n) a[i]=num[i]=read()+1,ans+=a[i]; 77 sort(num+1,num+n+1); 78 up(i,1,n) if(num[i]!=num[i-1]) Num[++top]=num[i]; 79 up(i,1,top) num[i]=Num[i]; 80 up(i,1,n) a[i]=find(a[i]); 81 } 82 void solve(){ 83 up(i,1,n){ 84 int pos=get(1,1,n); 85 updata(1,1,n,1,a[i],1); 86 if(a[i]+1<=pos-1) updata(1,1,n,a[i]+1,pos-1,-1); 87 } 88 int pos=get(1,1,n); 89 res(1,1,n); 90 up(i,1,pos) ans-=K[i]*(num[i]-num[i-1]); 91 printf("%lld ",ans); 92 } 93 int main(){ 94 freopen(FILE".in","r",stdin); 95 freopen(FILE".out","w",stdout); 96 init(); 97 solve(); 98 return 0; 99 }
写完这道题,忽然有一种代码进化的感觉,以前写的代码都不能看了