KMP学习 （洛谷 P3375 【模板】KMP字符串匹配）

题目地址：https://www.luogu.com.cn/problem/P3375

参考博客：https://www.cnblogs.com/stelayuri/p/12506196.html

关于kmp算法，其实之前就有接触，但是有关next数组迟迟不能清晰的理解，今天又做了一道模板题，感觉稍稍理清了一点点，如下：

Next[j]就是待匹配串（下面的T串）从T[0]开始到T[j]结尾的这个子串中，前缀和后缀相等时对应前缀/后缀的最大长度减1（减一的原因是因为字符串的下标是从0开始，减一后next里面的值就可以当下标来用了）
例子：（下标从0开始）
下标：0123456
S: ababaac
T: abaac
代码实现的时候j初始为-1，且每次比较都是拿T[j+1]和S[i]比较，
该例子中当i等于3，j等于2的时候，T[j+1]和S[i]匹配失败了，但是他们之前的T串中从0到j位都是匹配成功了的，
所以就可以利用已经匹配成功的这一段中最长相同的前缀和后缀，只要拿T串中到j为止的子串里面最长前缀（有与它相同的最长后缀）的后一位继续和s[i]作比较就好了。
即：
    ababaac
        abaac

题目描述

给出两个字符串 s_1s1​ 和 s_2s2​，若 s_1s1​ 的区间 [l, r][l,r] 子串与 s_2s2​ 完全相同，则称 s_2s2​ 在 s_1s1​ 中出现了，其出现位置为 ll。
现在请你求出 s_2s2​ 在 s_1s1​ 中所有出现的位置。

定义一个字符串 ss 的 border 为 ss 的一个非 ss 本身的子串 tt，满足 tt 既是 ss 的前缀，又是 ss 的后缀。
对于 s_2s2​，你还需要求出对于其每个前缀 s's′ 的最长 border t't′ 的长度。

输入格式

第一行为一个字符串，即为 s_1s1​。
第二行为一个字符串，即为 s_2s2​。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 s_2s2​ 在 s_1s1​ 中出现的位置。
最后一行输出 |s_2|∣s2​∣ 个整数，第 ii 个整数表示 s_2s2​ 的长度为 ii 的前缀的最长 border 长度。

输入输出样例

输入 #1复制

ABABABC
ABA

输出 #1复制

1
3
0 0 1 

说明/提示

样例 1 解释

。

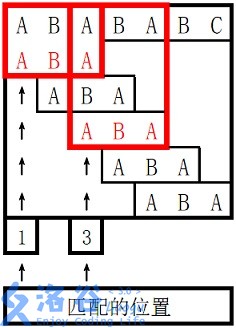对于 s_2s2​ 长度为 33 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 11。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

• Subtask 1（30 points）：|s_1| leq 15∣s1​∣≤15，|s_2| leq 5∣s2​∣≤5。
• Subtask 2（40 points）：|s_1| leq 10^4∣s1​∣≤104，|s_2| leq 10^2∣s2​∣≤102。
• Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 1 leq |s_1|,|s_2| leq 10^61≤∣s1​∣,∣s2​∣≤106，s_1, s_2s1​,s2​ 中均只含大写英文字母。

代码：

#include<bits/stdc++.h>
using namespace std;

string S,T;
int Slen,Tlen,Next[1000050];

void GetNext(){
    int i,j=-1;//初始为-1，因此后面的前缀和后缀相等时对应前缀/后缀的最大长度减了1
    Next[0]=-1;//这么写是因为字符串下标从0开始，而每次比较都是拿T[j+1]和S[i]比较，
    for(i=1;i<Tlen;i++){
        while(j>-1&&T[j+1]!=T[i])//j==-1的话表示不能再往前回溯了
            j=Next[j];//回溯
        if(T[j+1]==T[i])
            j++;
        Next[i]=j;
    }
}//模式串T的Next数组预处理

void KMP(){
    int i,j=-1;
    for(i=0;i<Slen;i++){
        while(j>-1&&T[j+1]!=S[i])
            j=Next[j];
        if(T[j+1]==S[i])
            j++;
        if(j==Tlen-1)
            cout<<i-Tlen+1+1<<endl;//多加一的原因还是因为下标从0开始，题目输出要求从1开始
    }
}//匹配模式串每次出现在主串中的位置

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>S;cin>>T;
    Slen=S.length(),Tlen=T.length();
    GetNext();
    KMP();
    for(int i=0;i<Tlen;i++)cout<<Next[i]+1<<" ";//输出border长度
    return 0;
}