Codeforces Round #315 (Div. 2)

A. Music

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Lesha loves listening to music via his smartphone. But the smartphone doesn't have much memory, so Lesha listens to his favorite songs in a well-known social network InTalk.

Unfortunately, internet is not that fast in the city of Ekaterinozavodsk and the song takes a lot of time to download. But Lesha is quite impatient. The song's duration is T seconds. Lesha downloads the first S seconds of the song and plays it. When the playback reaches the point that has not yet been downloaded, Lesha immediately plays the song from the start (the loaded part of the song stays in his phone, and the download is continued from the same place), and it happens until the song is downloaded completely and Lesha listens to it to the end. For q seconds of real time the Internet allows you to download q - 1 seconds of the track.

Tell Lesha, for how many times he will start the song, including the very first start.

Input

The single line contains three integers T, S, q (2 ≤ q ≤ 104, 1 ≤ S < T ≤ 105).

Output

Print a single integer — the number of times the song will be restarted.

Sample test(s)

input

5 2 2

output

2

input

5 4 7

output

1

input

6 2 3

output

1

Note

In the first test, the song is played twice faster than it is downloaded, which means that during four first seconds Lesha reaches the moment that has not been downloaded, and starts the song again. After another two seconds, the song is downloaded completely, and thus, Lesha starts the song twice.

In the second test, the song is almost downloaded, and Lesha will start it only once.

In the third sample test the download finishes and Lesha finishes listening at the same moment. Note that song isn't restarted in this case.

题解：追击问题嘛。。。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<stack>
#include<queue>
#include<cstring>
#define PAU putchar(' ')
#define ENT putchar('
')
using namespace std;
int T,S,q2,q1;
inline int read(){
    int x=0;bool sig=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-')sig=0;
    for(;isdigit(ch);ch=getchar())x=10*x+ch-'0';
    return sig?x:-x;
}
inline void write(int x){
    if(x==0){putchar('0');return;}if(x<0)putchar('-'),x=-x;
    int len=0,buf[20];while(x)buf[len++]=x%10,x/=10;
    for(int i=len-1;i>=0;i--)putchar(buf[i]+'0');return;
}
int main(){
    T=read();S=read();q2=read();q1=q2-1;
    if(S>=T){write(1);return 0;}
    int s2=0,s1=S,cur=1;
    while(true){
        int tim=s1-s2;int all=s2+tim*q2;if(all>=T){write(cur);break;}
        cur++;s1=all;
    }
    return 0;
}

B. Inventory

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Companies always have a lot of equipment, furniture and other things. All of them should be tracked. To do this, there is an inventory number assigned with each item. It is much easier to create a database by using those numbers and keep the track of everything.

During an audit, you were surprised to find out that the items are not numbered sequentially, and some items even share the same inventory number! There is an urgent need to fix it. You have chosen to make the numbers of the items sequential, starting with 1. Changing a number is quite a time-consuming process, and you would like to make maximum use of the current numbering.

You have been given information on current inventory numbers for n items in the company. Renumber items so that their inventory numbers form a permutation of numbers from 1 to n by changing the number of as few items as possible. Let us remind you that a set of n numbers forms a permutation if all the numbers are in the range from 1 to n, and no two numbers are equal.

Input

The first line contains a single integer n — the number of items (1 ≤ n ≤ 105).

The second line contains n numbers a1, a2, ..., an (1 ≤ ai ≤ 105) — the initial inventory numbers of the items.

Output

Print n numbers — the final inventory numbers of the items in the order they occur in the input. If there are multiple possible answers, you may print any of them.

Sample test(s)

input

3
1 3 2

output

1 3 2 

input

4
2 2 3 3

output

2 1 3 4 

input

1
2

output

1 

Note

In the first test the numeration is already a permutation, so there is no need to change anything.

In the second test there are two pairs of equal numbers, in each pair you need to replace one number.

In the third test you need to replace 2 by 1, as the numbering should start from one.

题解：一开始想复杂了，就是按位往里面塞东西就行。。。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<stack>
#include<queue>
#include<set>
#include<cstring>
#define PAU putchar(' ')
#define ENT putchar('
')
using namespace std;
const int maxn=100000+10,inf=-1u>>1;
struct data{int id,v;}A[maxn];bool operator<(const data&a,const data&b){return a.v<b.v||(a.v==b.v&&a.id<b.id);}
inline int read(){
    int x=0;bool sig=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-')sig=0;
    for(;isdigit(ch);ch=getchar())x=10*x+ch-'0';
    return sig?x:-x;
}
inline void write(int x){
    if(x==0){putchar('0');return;}if(x<0)putchar('-'),x=-x;
    int len=0,buf[20];while(x)buf[len++]=x%10,x/=10;
    for(int i=len-1;i>=0;i--)putchar(buf[i]+'0');return;
}
bool b[maxn];data t[maxn];int cnt,ans[maxn],bas[maxn],n;
int main(){
    n=read();
    for(int i=1;i<=n;i++)A[i].v=read(),A[i].id=i;
    sort(A+1,A+1+n);
    for(int i=1;i<=n;i++){
        if(1<=A[i].v&&A[i].v<=n&&!b[A[i].v]){
            b[A[i].v]=true;ans[A[i].id]=A[i].v;
        }else t[++cnt]=A[i];
    }int cur=1;
    //for(int i=1;i<=n;i++)write(ans[i]),PAU;ENT;
    for(int i=1;i<=n;i++){
        if(ans[i])write(ans[i]),PAU;
        else{
            while(b[cur])cur++;
            write(cur);PAU;b[cur++]=true;
        }
    }
//  int pos=lower_bound(A+1,A+1+n,n)-A-1;
//  for(int i=1;i<=n;i++){
//      if(1<=A[i]&&A[i]<=n){
//          if(!b[A[i]])b[A[i]]=true,ans[i]=A[i];
//          else t[cnt++]=A[i];
//      }else{
//          t[cnt++]=A[i];
//      }
//  }
//  for(int i=1;i<=n;i++){
//      
//  }
//  for(int i=1;i<=n;i++){
//      if(1<=A[i]&&A[i]<=n){
//          if(S.count(A[i]))ans++;
//          else S.insert(A[i]);
//      }else ans++;
//  }write(ans);
    return 0;
}

C. Primes or Palindromes?

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Rikhail Mubinchik believes that the current definition of prime numbers is obsolete as they are too complex and unpredictable. A palindromic number is another matter. It is aesthetically pleasing, and it has a number of remarkable properties. Help Rikhail to convince the scientific community in this!

Let us remind you that a number is called prime if it is integer larger than one, and is not divisible by any positive integer other than itself and one.

Rikhail calls a number a palindromic if it is integer, positive, and its decimal representation without leading zeros is a palindrome, i.e. reads the same from left to right and right to left.

One problem with prime numbers is that there are too many of them. Let's introduce the following notation: π(n) — the number of primes no larger than n, rub(n) — the number of palindromic numbers no larger than n. Rikhail wants to prove that there are a lot more primes than palindromic ones.

He asked you to solve the following problem: for a given value of the coefficient A find the maximum n, such that π(n) ≤ A·rub(n).

Input

The input consists of two positive integers p, q, the numerator and denominator of the fraction that is the value of A (, ).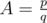

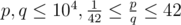Output

If such maximum number exists, then print it. Otherwise, print "Palindromic tree is better than splay tree" (without the quotes).

Sample test(s)

input

1 1

output

40

input

1 42

output

1

input

6 4

output

172

题解：噗。。。这道题枚举就行。。。做的时候在64位机上也得跑了3~4s，虚的不行，就去打表了，然后蹦了。。。

D. Symmetric and Transitive

time limit per test

1.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Johnny has recently learned about set theory. Now he is studying binary relations. You've probably heard the term "equivalence relation". These relations are very important in many areas of mathematics. For example, the equality of the two numbers is an equivalence relation.

A set ρ of pairs (a, b) of elements of some set A is called a binary relation on set A. For two elements a and b of the set A we say that they are in relation ρ, if pair 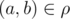, in this case we use a notation .

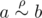Binary relation is equivalence relation, if:

1. It is reflexive (for any a it is true that );
2. It is symmetric (for any a, b it is true that if 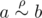, then );
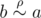3. It is transitive (if 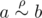 and 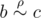, than ).

Little Johnny is not completely a fool and he noticed that the first condition is not necessary! Here is his "proof":

Take any two elements, a and b. If 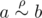, then  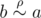(according to property (2)), which means  (according to property (3)).

It's very simple, isn't it? However, you noticed that Johnny's "proof" is wrong, and decided to show him a lot of examples that prove him wrong.

Here's your task: count the number of binary relations over a set of size n such that they are symmetric, transitive, but not an equivalence relations (i.e. they are not reflexive).

Since their number may be very large (not 0, according to Little Johnny), print the remainder of integer division of this number by109 + 7.

Input

A single line contains a single integer n (1 ≤ n ≤ 4000).

Output

In a single line print the answer to the problem modulo 109 + 7.

Sample test(s)

input

1

output

1

input

2

output

3

input

3

output

10

Note

If n = 1 there is only one such relation — an empty one, i.e. 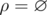. In other words, for a single element x of set A the following is hold: .

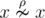If n = 2 there are three such relations. Let's assume that set A consists of two elements, x and y. Then the valid relations are 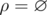,ρ = {(x, x)}, ρ = {(y, y)}. It is easy to see that the three listed binary relations are symmetric and transitive relations, but they are not equivalence relations.

题解：ans[n] = Bell[n +１] - Bell[n];呵呵哒。。。