第二章 分治算法 上

分治算法的原理

设计过程：

Divide：整个问题划分为多个子问题——分解

Conquer：求解各个子问题（递归调用子问题的算法）——求解

Combine：合并子问题的解，形成原始问题的解。——合并

分析过程：

1、建立递归方程：

　　T(n)=aT(n/b)+D(n)+C(n)

　　　　Divide时间复杂度：D(n)

　　　　Conquer时间复杂度：aT(n/b)

　　　　Combine：C(n)

　　当n<c，T(n)=θ(1)

2、递归方程求解：

归并算法：

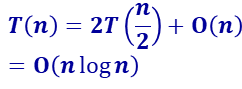
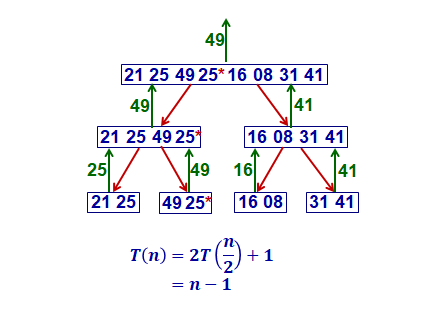
找最大值：

 

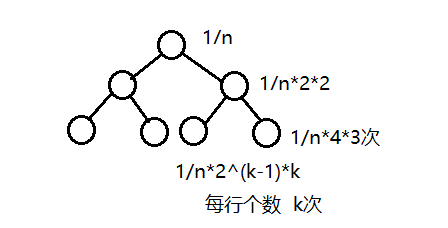
折半搜索：

最坏情况：T(n)=T(n/2)+O(1)

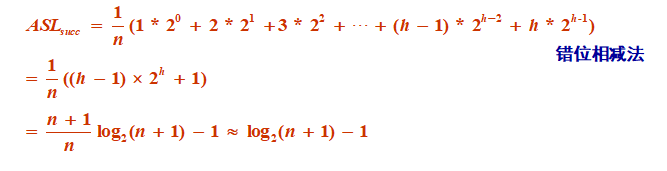
大整数乘法

 

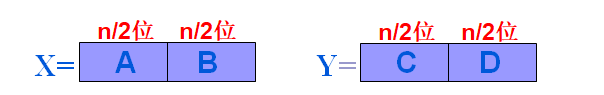
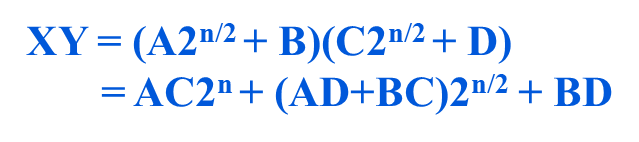
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  =AC2^n+AD2^(n/2)+BC*2^(n/2)+BD

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  分解成了四个规模是n/2的子问题4T(n/2)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　AC2^n——2n的规模的数字

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　AD2^(n/2)——(3/2n)的规模的数字

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　BC2^(n/2)——(3/2n)的规模的数字

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　BD——n规模的数字

上述四项相加的复杂度为O(6n)

所以

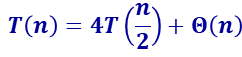
利用master定理可以计算时间复杂度为O(n^2)

由于通用算法的时间复杂度为O(n^2)，所以此算法并没有改善时间复杂度。

下面换一种算法：

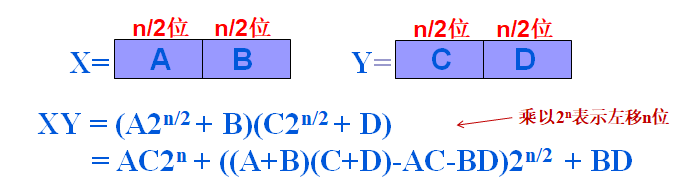
　　　　　　　　　　　　　　　　　　　　　　1、分解成了三个规模是n/2的乘法

　　　　　　　　　　　　　　　　　　　　　　2、合并代价依旧是O(n)

快速排序：

最好情况T(n)=2T(n/2)+O(n)

最坏情况T(n)=T(1)+T(n-1)+O(n)

基于比较排序方法最好的算法不会好于O(nlogn)

因为比较搜索树中2^h>=n!，从而h>=nlogn

第k小的元素

在有n个元素的数组中找第k小的元素

Select (S,k)

if |S|<50，排序输出第k小，return.

S划分5个元素一组，每小组取出中位数。

将中位数放入数组M中，有n/5个

X=Select(M,|M|/2)——找中位数的中位数

A是S中比X小的元素

B是S中与X相等的元素

C是S中大于X的元素

if|A|>=k :select(A,k)

elseif |A|+|B|>=k  X

else:select(C,k-|A|-|B|)