哈夫曼树与哈夫曼编码

哈夫曼树是一种简单的树结构，建树过程如下：

给出一组数据，不断选择最小的两个数，并用两个数的和作为它们的parent节点，再从数据中删除这两个数，将两个数的和加入数据中，直到所有的数据都被加入树结构，形成一颗树。

这颗树的所有非叶子节点都有两个child，两个child的值的和则是这个节点的值，根节点是初始数据的总和。

哈夫曼树有多种用途，这里讲解一下哈夫曼编码。

哈夫曼编码是将所给数据生成哈夫曼树后，从根节点开始，给每个节点的left child添加一位编码0，right child添加一位编码1，如图，编码完成后，则每个节点有了对应的二进制编码，如图中值为2的节点编码为010100，值为13的节点编码为00.

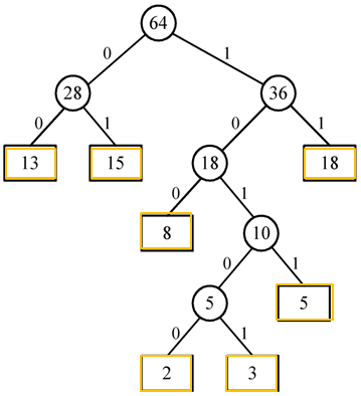
哈夫曼树有广泛的应用，例如在建立字库时，根据每个字符的使用频率，将使用频率高的字符编一个较短的编码，而将使用频率低的字符编一个较大的编码，来有效的节省空间。下面我展示一下哈夫曼编码的代码。

#pragma once
#include <queue>
#include <string>

int huffman_N;
std::string huffman_code_res[MAX_N];

struct Node
{
    int id, freq, left, right;
    void init(int i, int f)
    {
        id = i;
        freq = f;
        left = right = INF;
    }
    bool operator<(const Node &a) const
    {
        return a.freq < freq;
    }
} huffman_node[2 * MAX_N];

void add_huffman_code(Node tmp)
{
    huffman_code_res[tmp.left] = huffman_code_res[tmp.id] + "0";
    huffman_code_res[tmp.right] = huffman_code_res[tmp.id] + "1";
    if (huffman_node[tmp.left].left != INF) add_huffman_code(huffman_node[tmp.left]);
    if (huffman_node[tmp.right].left != INF) add_huffman_code(huffman_node[tmp.right]);
}

void make_huffman_tree()
{
    std::priority_queue<Node> pq;
    for (int i = 0;i < huffman_N;++i)
    {
        pq.push(huffman_node[i]);
        huffman_code_res[i] = "";
    }
    Node a, b;
    while (!pq.empty())
    {
        a = pq.top();pq.pop();
        if (pq.empty()) break;
        b = pq.top();pq.pop();
        huffman_node[a.id + huffman_N] = { a.id + huffman_N,a.freq + b.freq,a.id,b.id };
        pq.push(huffman_node[a.id + huffman_N]);
    }
    add_huffman_code(a);
}

之后我用图中树进行一次测试：

void huffman_codeTest()
{
    cin >> huffman_N;
    for (int i = 0;i < huffman_N;++i)
    {
        int tmp;
        cin >> tmp;
        huffman_node[i].init(i, tmp);
    }
    make_huffman_tree();
    for (int i = 0;i < huffman_N;++i)
        cout << i << " " << huffman_node[i].freq << " " << huffman_code_res[i] << endl;
}

测试结果如下：

7
2 3 5 8 13 15 18
0 2 11110
1 3 11111
2 5 1110
3 8 110
4 13 00
5 15 01
6 18 10
请按任意键继续. . .

可以看到，虽然由于建树顺序的差别，和图中编码有所不同，但是位数一致，哈夫曼树成功的按照使用频率的区别给不同的id进行了编码。根据结果来推断，这棵树的样子是下面这样：