1.问题描述
旅行商问题(Travelling Salesman Problem, 简记TSP,亦称货郎担问题):设有n个城市和距离矩阵D=[dij],其中dij表示城市i到城市j的距离(i,j=1,2 … n),则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。
2.算法设计
对原问题进行分析,TSP的一个解可表述为一个循环排列:
Π= (Π1,Π2,Π3… Πn),即
Π1→ Π2→ … → Πn→ Π1
有(n-1)!/2 种不同方案,若使用穷举法,当n很大时计算量是不可接受的。旅行商问题综合了一大类组合优化问题的典型特征,属于NP难题,不能在多项式时间内进行检验。若使用动态规划的方法时间复杂性和空间复杂性都保持为n的指数函数。
本次实验利用模拟退火算法(Simulated Annealing)求解TSP问题。模拟退火算法最早由N.Metropolis等人于1953年提出,基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。该算法从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间随机寻找全局最优解。
退火是将固体加热到足够高的温度,使分子呈随机排列态,然后逐步降温冷却,最后分子以低能状态排列,得到稳定状态的固体。退火的过程有:
(1)加温过程:增强粒子运动,消除系统原本可能存在的非均匀态;
(2)等温过程:对于与环境换热而温度不变的封闭系统,系统状态的自发变化总是朝向自由能减少的方向进行,当自由能达到最小时,系统平衡;
(3)冷却过程:使粒子热运动减弱并逐渐趋于有序,系统能量逐渐下降,从而得到低能的晶体结构。
其中,固体在恒温下达到热平衡的过程采用Metropolis方法进行模拟:
温度恒定为T时,当前状态i转为新状态j,如果j状态的能量小于i,则接受状态j为当前状态;否则,如果概率p=exp{-(Ej-Ei)/(k*T)}大于[0,1)区间的随机数,则仍接受状态j为当前状态;若不成立则保留状态i为当前状态。
温度变化时,由于p=exp{-(Ej-Ei)/(k*T)},因此在高温下,可接受当前状态能量差较大的新状态;在低温下,只接受与当前状态能量差较小的新状态。
退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。
我们使用模拟退火算法实现TSP的参数选取如下:
控制参数初值:t0 = 2000
停止准则:连续2个Mapkob链中对路径无任何变动(优化或恶化的)时即停止算法运行。
冷却进度表中的控制参数t的衰减函数:α(t)=0.98 * t
Mapkob链长:定长20000
新解的产生:随机交换两个序号。任选序号u和v (u<v),将u和v的顺序交换。
(Π1 …Πu-1ΠuΠu+1 …Πv-1ΠvΠv+1… Πn)
变为
(Π1 …Πu-1ΠvΠu+1 …Πv-1ΠuΠv+1… Πn)
3.程序流程

4.核心伪代码
Begin:
INITIALIZE; { 初始化i0= Π1 …Πn, t0=2000, L= 20000 }
randomize; { 初始化随机数种子}
Repeat
bChange:=0;
for l:=1 to L do
begin:
GENERATE; { 随机交换两个序号产生新的路径}
CALCULATE(df); { 计算df= f(j)-f(i) 的值}
if ACCEPT(t, df) then { 根据Metropolis准则判断是否接受新的路径}
begin
f: = f + df; { 计算已接受的路径的长度}
bChange:= 1;
end;
end;
t:=t * 0.9; { 衰减函数α(t)=0.98 * t }
if (bChange= 0) then s:=s+1 else s:=0;
until s = 2 { 停止准则为连续两个Mapkob链路径无变化}
End;
5.代码运行及测试
运行环境:VS2013,Windows 10系统
输入说明:
第一行输入需要遍历的城市数目num,之后的num行输入邻接矩阵用于描述城市两两之间的距离。
输出说明:输出包括最短路径回路和最短路径的距离。
程序运行结果:
(1)
程序输入:

程序输出1:
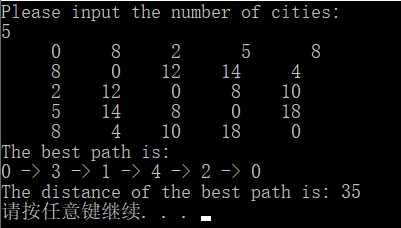
程序输出2:

程序输出3:
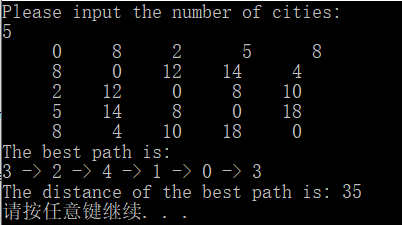
(2)
程序输入:

程序输出1:
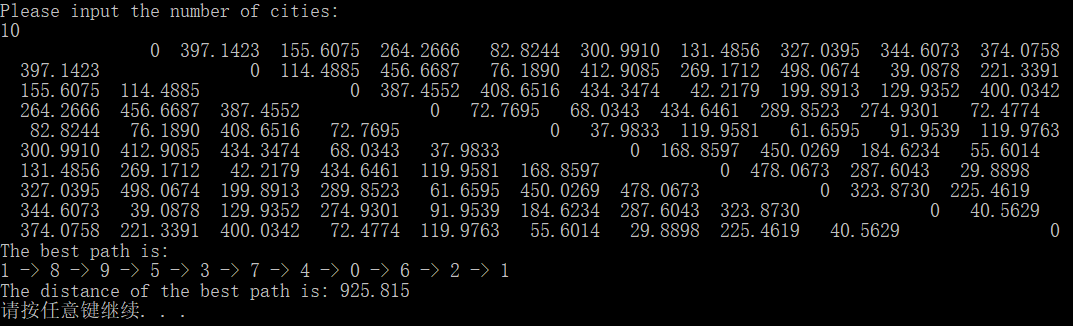
程序输出2:
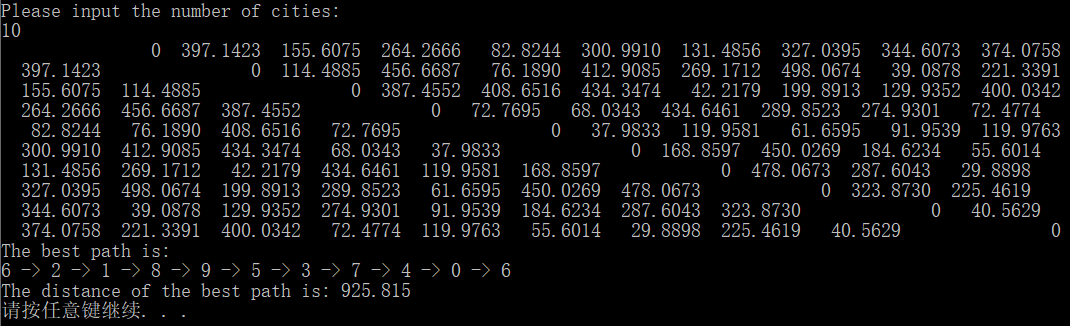
程序输出3:
由上述实验结果可知,如果全局最优解不唯一,那么对于同一组输入数据,多次运行得到的路径也不相同。SA算法的效果依赖于链长、温度变化范围、控制参数等等,如果参数选取不合适将不能得到好的解。此外,实验过程中发现,在当前的参数(t0=2000,L=20000,alpha=0.98)情况下,问题规模很小时耗费时间较长,而当问题规模较大时耗费时间明显减少,可见模拟退火算法在大规模问题下的高效性。
6.结论
本次实验采用模拟退火算法解决TSP问题,该算法具有超越算法本身的启发式意义。模拟退火算法将自然物理过程中的固体退火过程与组合优化问题进行类比,成功地将退火过程迁移用于组合优化问题,不仅应用范围广、使用灵活,而且初始化条件少。但是收敛速度较慢,运行时间较长。模拟退火算法是在状态空间搜索近似最优解的过程,由于搜索过程中会以一定概率接受更差的结果,所以能够跳出局部最优状态范围。
源码:
#include <iostream> #include <time.h> #include <math.h> using namespace std; #define MAX_CITY_NUM 100 #define T0 2000 #define T 1e-5 #define ALPHA 0.98 #define L 20000 struct path{ int route[MAX_CITY_NUM]; double dis; }; double w[MAX_CITY_NUM][MAX_CITY_NUM]; int num; double s = 0; path p0; void Init_City() { cout << "Please input the number of cities:" << endl; cin >> num; for (int i = 0; i < num; ++i) for (int j = 0; j < num; ++j) cin >> w[i][j]; } void Init_path() { p0.dis = 0; for (int i = 0; i < num; ++i) { p0.route[i] = i; if (i != num - 1) p0.dis += w[i][i + 1]; } p0.dis += w[num - 1][0]; } path generate(path p) { int x = 0, y = 0; while (x == y) { x = (int)(num * (rand() / (RAND_MAX + 1.0))); y = (int)(num * (rand() / (RAND_MAX + 1.0))); } path gen = p; int tmp; tmp = gen.route[x]; gen.route[x] = gen.route[y]; gen.route[y] = tmp; gen.dis = 0; for (int i = 0; i < num - 1; ++i) gen.dis += w[gen.route[i]][gen.route[i + 1]]; gen.dis += w[gen.route[num - 1]][gen.route[0]]; return gen; } void TSP_SA() { double t = T0; srand(time(NULL)); path cur = p0; path next = p0; int bChange; while (t > T) { bChange = 0; for (int i = 0; i < L; ++i) { next = generate(cur); double df = next.dis - cur.dis; if (df <= 0) { cur = next; bChange = 1; } else { double rndp = rand() / (RAND_MAX + 1.0); double eps = exp(-df / t); if (eps > rndp && eps < 1) { cur = next; bChange = 1; } } } if (cur.dis < p0.dis) p0 = cur; t *= ALPHA; if (!bChange) ++s; else s = 0; if (s == 2) break; } } int main() { Init_City(); Init_path(); TSP_SA(); cout << "The best path is:" << endl; for (int i = 0; i < num; ++i) cout << p0.route[i] << " -> "; cout << p0.route[0] << endl; cout << "The distance of the best path is: " << p0.dis << endl; system("pause"); return 0; }