题目链接:https://leetcode.com/problems/largest-rectangle-in-histogram/description/
题目大意:在直方图中找出最大的矩形面积。例子如下:
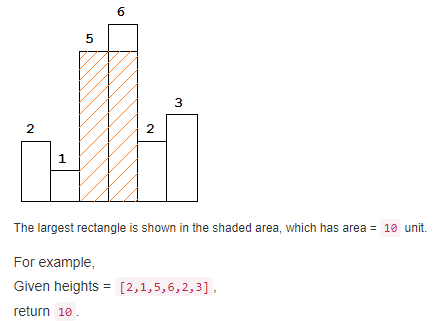
法一:暴力,无任何优化,超时了。对于每个高度,分别向左和向右查找能到达的最远下标(在目前的高度情况下)。代码如下:

1 public int largestRectangleArea(int[] heights) { 2 int ma = 0; 3 for(int i = 0; i < heights.length; i++) { 4 //向左 5 int left = i; 6 for(; left >= 0 && heights[left] >= heights[i]; left--); 7 //向右 8 int right = i; 9 for(; right < heights.length && heights[right] >= heights[i]; right++); 10 int sum = (right - left - 1) * heights[i]; 11 if(sum > ma) { 12 ma = sum; 13 } 14 } 15 return ma; 16 }
法二:换了一种思维方式的暴力,依旧超时。不再从中间向两边扩展,而是每到一个点,就找其局部峰值,然后由局部峰值点向前查找每个矩形面积,比较得最大值。代码如下:

1 public int largestRectangleArea(int[] heights) { 2 int ma = 0; 3 for(int i = 0; i < heights.length; i++) { 4 //找局部峰值 5 //如果不是目前峰值,则跳过 6 if(i + 1 < heights.length && heights[i] < heights[i + 1]) { 7 continue; 8 } 9 //如果是目前峰值,则向前计算矩形,会将目前峰值前面所有可能的矩形面积都计算一遍 10 //所以虽然这个方法没有在每个点上向左右两边扩展计算所有可能的矩形面积,但是其实也变相计算了所有可能的矩形面积,只是换了种思维方式 11 int mi = heights[i]; 12 for(int j = i; j >= 0; j--) { 13 mi = Math.min(mi, heights[j]); 14 int sum = mi * (i - j + 1); 15 ma = Math.max(ma, sum); 16 } 17 } 18 return ma; 19 }
法三:用stack优化暴力,其实也计算了所有可能的矩形面积,只是优化了遍历方式,据说时间复杂度是o(n)?比较怀疑。代码如下(耗时23ms):

1 public int largestRectangleArea(int[] heights) { 2 //stack中存递增高度 3 Stack<Integer> s = new Stack<Integer>(); 4 int ma = 0; 5 for(int i = 0; i < heights.length; i++) { 6 //如果栈顶高度比当前高度高,则退栈 7 //由目前栈顶高度向右计算可能的最大矩形面积,其实最终也把每个点所有可能的矩形面积都计算了一遍,但是由于优化计算,效率上好了很多 8 while(!s.isEmpty() && heights[s.peek()] >= heights[i]) { 9 int cur = s.pop(); 10 //计算矩形面积 11 ma = Math.max(ma, heights[cur] * (s.isEmpty() ? i : (i - s.peek() - 1))); 12 } 13 //如果与栈顶是递增关系,则压栈 14 s.push(i); 15 } 16 //由于最后stack中必定存在一个递增序列,因为在最后一次s.push(i)之后,没有计算,所以要将此递增序列计算完 17 while(!s.isEmpty()) { 18 int cur = s.pop(); 19 ma = Math.max(ma, heights[cur] * (s.isEmpty() ? heights.length : (heights.length - s.peek() - 1))); 20 } 21 return ma; 22 }
