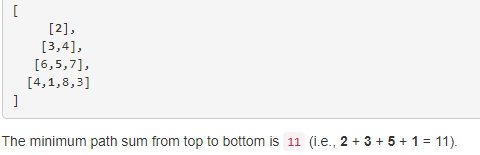
题目大意:给出一个三角矩阵,求解从顶端到底端的最短路径和(空间复杂度最好是o(n))。例子如下:
法一:二维DP。dp[i][j]表示第i行第i列,从下到当前位置的最短路径和。公式:dp[i][j] = Math.min(dp[i+1][j], dp[i+1][j+1])+当前值。从下到上依次计算即可。代码如下(耗时7ms):

1 public int minimumTotal(List<List<Integer>> triangle) { 2 int row = triangle.size(); 3 int[][] dp = new int[row][row]; 4 //初始化最后一行 5 for(int i = 0; i < row; i++) { 6 dp[row - 1][i] = triangle.get(row - 1).get(i); 7 } 8 //从倒数第二行往上逐行进行计算 9 for(int i = row - 2; i >= 0; i--) { 10 for(int j = 0; j <= i; j++) { 11 dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle.get(i).get(j); 12 } 13 } 14 return dp[0][0]; 15 }
法二:一维DP。与二维DP完全类似,只是把外层的空间略去了,因为内层每次dp都依托外层的计算,所以公式就是:dp[j]=Math.min(dp[j],dp[j+1])+当前值。代码如下(耗时8ms):

1 public int minimumTotal(List<List<Integer>> triangle) { 2 int row = triangle.size(); 3 int[] dp = new int[row]; 4 //初始化 5 for(int i = 0; i < row; i++) { 6 dp[i] = triangle.get(row - 1).get(i); 7 } 8 //逐行计算 9 for(int i = row - 2; i >= 0; i--) { 10 for(int j = 0; j <= i; j++) { 11 dp[j] = Math.min(dp[j], dp[j + 1]) + triangle.get(i).get(j); 12 } 13 } 14 return dp[0]; 15 }
