96. Unique Binary Search Trees

题目链接

题目大意：1~n的自然数，可以组成多少个不同的二叉搜索树。例子如下：

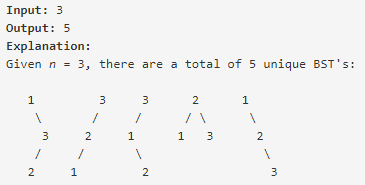
法一：卡特兰数。通项公式C(2n, n)/(n+1)=C(2n, n) - C(2n, n+1)。代码如下（耗时0ms）：

    public int numTrees(int n) {
        //卡特兰数
        //C(2n, n)/(n+1)
        long res = 1;
        for(int i = n + 1; i <= n * 2; i++) {
            res = res * i / (i - n);
        }
        return (int)(res / (n + 1));
    }

法二：DP。利用的也是卡特兰数。代码如下（耗时0ms）：

    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++) {
            for(int j = 0; j < i; j++) {
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }