20182334 2019-2020-1 《数据结构与面向对象程序设计》第九周学习总结
教材学习内容总结
第九周我学习到的内容有:
- 树
- 树的遍历
- 二叉树的实现
- 决策树
- 中序和先序构成后树
- 堆排序
- 二叉排序树
树
树是非线性结构,其元素组织为一个结构层次。
计算树高度的代码为:
public int height(){
return height(root);
}
public int height(BinaryNode<T> root){
if(root==null)
return 0;
int L_height=height(root.left);
int R_height=height(root.right);
return (L_height>=R_height)?L_height+1:R_height+1;
}
树的遍历
- 先序遍历 :访问根,自左至右遍历子树。
public void preOrder(Node root)
{ // 前序遍历
if (root != null)
{
System.out.print(root.data + " ");
preOrder(root.left);
preOrder(root.right);
}
}
- 中序遍历:遍历左子树,然后访问根,然后自左至右遍历余下的各个子树。
public void inOrder(Node root)
{ // 中序遍历
if (root != null)
{
inOrder(root.left);
System.out.print(root.data + " ");
inOrder(root.right);
}
}
- 后序遍历:自左至右遍历各子树,然后访问根。
public void postOrder(Node root)
{ // 后序遍历
if (root != null)
{
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data + " ");
}
}
- 层序遍历:从树的顶层到底层,从左至右,访问树中每层的每个结点。
public void levelOrder() {
BiTNode<E> node =root;
LinkedList<BiTNode<E>> list = new LinkedList<>();
list.add(node);
while(!list.isEmpty()) {
node=list.poll();
System.out.print(node.data);
if(node.lchild!=null)
list.offer(node.lchild);
if(node.rchild!=null)
list.offer(node.rchild);
}
}
二叉树的实现
以下是实现的代码:
public void creat(Object[] objs){
datas=new ArrayList<bintree>();//将一个数组的值依次转换为Node节点
for(Object o:objs){
datas.add(new bintree(o)); }//第一个数为根节点
root=datas.get(0);//建立二叉树
for (int i = 0; i <objs.length/2; i++) {//左孩子
datas.get(i).left=datas.get(i*2+1);//右孩子
if(i*2+2<datas.size()){//避免偶数的时候下标越界
datas.get(i).right=datas.get(i*2+2);
}
}
}
决策树
用例子来说明一个决策树:
import javafoundations.*;
import java.util.Scanner;
public class asd
{
private LinkedBinaryTree<String> tree;
public asd()
{
String e1 = "TA是个人";
String e2 = "TA是男性,再猜一遍!";//N
String e4 = "他很帅!!再猜一遍!!";//N
String e8 = "怎么这都猜错?再来一次!!";//N
String e16 = "我的天还错??!!行吧再给你一条,他较高,再猜一遍!";
String e18 = "你大爷!TA是1823班的!再猜一遍!";
String e20 = "服了,TA是1823最帅的那个,再猜一遍!";
String e22 = "......拜托你好好想想,再猜一遍!";
String e24 = "...再想想??再猜一遍!";
String e26 = "..come on 拜托!再来!";
String e28 = "712最帅的那个!再猜一遍";
String e30 = "算了你别猜了,赶紧洗洗睡吧!";
String e31 = "你大爷!终于猜出来了!还是值得表扬!";
String e29 = "你能猜这么久也是没谁了。";
String e27 = "哥你终于对了";
String e25 = "邹佳伟?? 就这麦?怎么可能有姬旭帅?还算你有眼光";
String e23 = "没错,姬旭是最帅的,其他男人怎么能比得过呢???搞不懂你为啥选这么久,气死为父了!!";
String e21 = "还行";
String e19 = "算你还不错!";
String e17 = "你可真不容易,终于对了!";
String e9 = "有眼光!!姬旭天下第一帅!!";//Y
String e5 = "!!!bingo!!!";//Y
String e3 = "!!!bingo!!!";//Y
LinkedBinaryTree<String> n2, n3, n4, n5, n8, n9,
n17,n16,n18,n19,n20,n21,n22,n23,n24,n25,
n26,n27,n28,n29,n30,n31;
n31 = new LinkedBinaryTree<String>(e31);
n30 = new LinkedBinaryTree<String>(e30);
n29 = new LinkedBinaryTree<String>(e29);
n28 = new LinkedBinaryTree<String>(e28,n30,n31);
n27 = new LinkedBinaryTree<String>(e27);
n26 = new LinkedBinaryTree<String>(e26,n28,n29);
n25 = new LinkedBinaryTree<String>(e25);
n24 = new LinkedBinaryTree<String>(e24,n26,n27);
n23 = new LinkedBinaryTree<String>(e23);
n22 = new LinkedBinaryTree<String>(e22,n24,n25);
n21 = new LinkedBinaryTree<String>(e21);
n20 = new LinkedBinaryTree<String>(e20,n22,n23);
n19 = new LinkedBinaryTree<String>(e19);
n18 = new LinkedBinaryTree<String>(e18,n20,n21);
n16 = new LinkedBinaryTree<String>(e16,n18,n19);
n17 = new LinkedBinaryTree<String>(e17);
n8 = new LinkedBinaryTree<String>(e8,n16,n17);
n9 = new LinkedBinaryTree<String>(e9);
n4 = new LinkedBinaryTree<String>(e4, n8, n9);
n5 = new LinkedBinaryTree<String>(e5);
n2 = new LinkedBinaryTree<String>(e2, n4, n5);
n3 = new LinkedBinaryTree<String>(e3);
tree = new LinkedBinaryTree<String>(e1, n2, n3);
}
public void diagnose()
{
Scanner scan = new Scanner(System.in);
LinkedBinaryTree<String> current = tree;
System.out.println ("开始竞猜!!");
while (current.size() > 1)
{
System.out.println (current.getRootElement());
String a = scan.nextLine();
if (a.equalsIgnoreCase("姬旭"))
current = current.getRight();
else
current = current.getLeft();
}
System.out.println (current.getRootElement());
}
}
中序和先序构造后序
public Node<E> CreatTree(E[] array){
nodeList = new LinkedList<Node>();
for (int i = 0 ; i < array.length ; i++ ){
nodeList.add(new Node(array[i]));
}
for(int j = 0;j<(array.length/2-1);j++){
nodeList.get(j).setLeft(nodeList.get(j*2+1));
nodeList.get(j).setright(nodeList.get(j*2+2));
}
int index = array.length/2-1;
nodeList.get(index).setLeft(nodeList.get(index*2+1));
if(array.length%2 == 1){
nodeList.get(index).setright(nodeList.get(index*2+2));
}
root = nodeList.get(0);
return root;
}
堆排序
public class Sort {
public static void main(String[] args) {
int[] nums = {16,7,3,20,17,8};
headSort(nums);
for (int num : nums) {
System.out.print(num + " ");
}
}
/**
* 堆排序
*/
public static void headSort(int[] list) {
//构造初始堆,从第一个非叶子节点开始调整,左右孩子节点中较大的交换到父节点中
for (int i = (list.length) / 2 - 1; i >= 0; i--) {
headAdjust(list, list.length, i);
}
//排序,将最大的节点放在堆尾,然后从根节点重新调整
for (int i = list.length - 1; i >= 1; i--) {
int temp = list[0];
list[0] = list[i];
list[i] = temp;
headAdjust(list, i, 0);
}
}
private static void headAdjust(int[] list, int len, int i) {
int k = i, temp = list[i], index = 2 * k + 1;
while (index < len) {
if (index + 1 < len) {
if (list[index] < list[index + 1]) {
index = index + 1;
}
}
if (list[index] > temp) {
list[k] = list[index];
k = index;
index = 2 * k + 1;
} else {
break;
}
}
list[k] = temp;
}
}
堆排序有最大堆,最小堆。
- 最大堆:非叶子节点比左右子节点要大
- 最小堆: 非叶子节点比左右子节点要小
为了使大家更明白,这里放一张图:

二叉排序树
二叉排序树构造起来很简单,但是在删除方法的部分比较困难,在思考算法的时候有很多问题,以下是整个排序树,里面包含查找、排序、插入、删除等各种方法。
public class BinarySearchTree
{ // 二叉搜索树类
private class Node
{ // 节点类
int data; // 数据域
Node right; // 右子树
Node left; // 左子树
}
private Node root; // 树根节点
public void insert(int key)
{
Node p = new Node(); //待插入的节点
p.data =key;
if(root==null)
{
root=p;
}
else
{
Node parent = new Node();
Node current=root;
while(true)
{
parent=current;
if(key>current.data)
{
current=current.right; // 右子树
if(current==null)
{
parent.right=p;
return;
}
}
else
{
current=current.left; // 左子树
if(current==null)
{
parent.left=p;
return;
}
}
}
}
}
public void preOrder(Node root)
{ // 前序遍历
if (root != null)
{
System.out.print(root.data + " ");
preOrder(root.left);
preOrder(root.right);
}
}
public void inOrder(Node root)
{ // 中序遍历
if (root != null)
{
inOrder(root.left);
System.out.print(root.data + " ");
inOrder(root.right);
}
}
public void postOrder(Node root)
{ // 后序遍历
if (root != null)
{
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data + " ");
}
}
public Node find(int key)
{ // 从树中按照关键值查找元素
Node current = root;
while (current.data != key)
{
if (key > current.data)
current = current.right;
else
current = current.left;
if (current == null)
return null;
}
return current;
}
public void show(Node node)
{ //输出节点的数据域
if(node!=null)
System.out.println(node.data);
else
System.out.println("null");
}
private Node getSuccessor(Node delNode) //寻找要删除节点的中序后继结点
{
Node successorParent=delNode;
Node successor=delNode;
Node current=delNode.right;
//用来寻找后继结点
while(current!=null)
{
successorParent=successor;
successor=current;
current=current.left;
}
//如果后继结点为要删除结点的右子树的左子,需要预先调整一下要删除结点的右子树
if(successor!=delNode.right)
{
successorParent.left=successor.right;
successor.right=delNode.right;
}
return successor;
}
public boolean delete(int key) // 删除结点
{
Node current = root;
Node parent = new Node();
boolean isRightChild = true;
while (current.data != key)
{
parent = current;
if (key > current.data)
{
current = current.right;
isRightChild = true;
}
else
{
current = current.left;
isRightChild = false;
}
if (current == null) return false; // 没有找到要删除的结点
}
// 此时current就是要删除的结点,parent为其父结点
// 要删除结点为叶子结点
if (current.right == null && current.left == null)
{
if (current == root)
{
root = null; // 整棵树清空
}
else
{
if (isRightChild)
parent.right = null;
else
parent.left = null;
}
return true;
}
//要删除结点有一个子结点
else if(current.left==null)
{
if(current==root)
root=current.right;
else if(isRightChild)
parent.right=current.right;
else
parent.left=current.right;
return true;
}
else if(current.right==null)
{
if(current==root)
root=current.left;
else if(isRightChild)
parent.right=current.left;
else
parent.left=current.left;
return true;
}
//要删除结点有两个子结点
else
{
Node successor=getSuccessor(current); //找到要删除结点的后继结点
if(current==root)
root=successor;
else if(isRightChild)
parent.right=successor;
else
parent.left=successor;
successor.left=current.left;
return true;
}
}
教材学习中的问题和解决过程
-
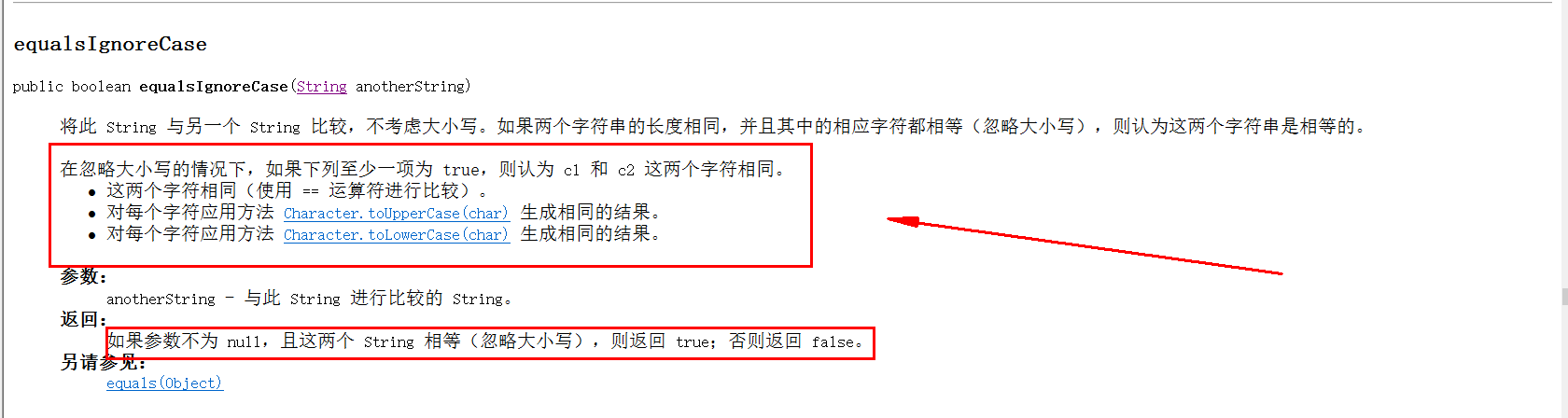
问题1:在设计决策树时,书上代码出现equalIgnoreCase,我不知道它和equal有什么区别?

-
问题1解决方案:上api jdk 上查了一下,发现原来equal是要完全相等,但equalIgnoreCase是不考虑大小写的,其实本质上都是一样的,,只不过是不看大小写了,这点对于用户输入Y或者y时有很大的帮助,省略了很多代码,可能这是java的好处吧!

-
问题2:不知道平衡二叉查找树有什么用,如果不用会有什么影响?
-
问题2解决方案:为了解决这个问题,我上网看了看别人的博客,发现了一个讲解:二叉查找树与平衡二叉树
那么什么是平衡二叉树呢?
平衡二叉搜索树,又被称为AVL树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
由于普通的二叉查找树会容易失去”平衡“,极端情况下,二叉查找树会退化成线性的链表,导致插入和查找的复杂度下降到 O(n) ,所以,这也是平衡二叉树设计的初衷。那么平衡二叉树如何保持”平衡“呢?根据定义,有两个重点,一是左右两子树的高度差的绝对值不能超过1,二是左右两子树也是一颗平衡二叉树。
如下图所示,左图是一棵平衡二叉树,根节点10,左右两子树的高度差是1,而右图,虽然根节点左右两子树高度差是0,但是右子树15的左右子树高度差为2,不符合定义,所以右图不是一棵平衡二叉树。

-
问题3:堆排序有两种方法,一直搞不清两者的区别和各自的优势。
-
问题3解决方案:还是上网找博客,看到一篇java堆排序
堆排序分为最大堆和最小堆,所谓最大堆,就是非叶子结点比左右子节点要大,所谓 最小堆,就是非叶子节点比左右子节点要小。
以构建最大堆为例,堆排序的过程:
-
1、原始数组形成一个顺序堆。数组中下标索引为i的节点,左节点是i2 +1,右节点是i2+2
-
2、初始化堆,从最后一个叶子节点的父节点开始一层层向上遍历,使得每一对父子节点中的最大节点上浮,维持最大堆的性质。
如果有交换位置的操作,那么要以交换后的新子节点为父节点递归遍历,以维持该分支上的最大堆性质。直到遍历到根节点,此时根节点最大。
- 3、排序阶段:将根节点与最后一个叶子节点交换位置,交换过位置的尾部叶子节点就是从小到大的排序,最后的叶子节点的索引相对应也减1。
然后以根节点,维护最大堆性质,同样的,如果有交换位置的操作,那么要以被交换的子节点为父节点递归遍历,以维持该分支上的最大堆性质
堆排序的核心点在于:如果有交换位置的操作,那么要以交换后的新子节点为父节点递归遍历,以维持该分支上的最大堆性质
代码调试中的问题和解决过程
-
问题1:如下图,这里的getRight方法不知道为什么不对,怎么调也不对。

-
问题1解决方案:仔细看报错的原因,原来是因为它调用的方法里定义的变量不对:
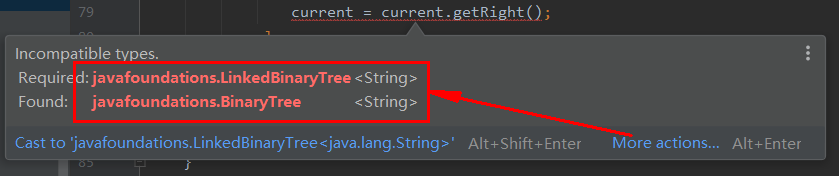
少了Linked,所以一直错,于是我到对应的类里去看,果然发现,getLeft和getRight两个方法定义的变量不同:

改正问题之后,发现原来都是细节地方出错,实在是不应该。
- 问题2:在通过中序和先序创造后序时,不知道怎么用代码实现。那棵树不知道怎么联合建起来。
String preOrder[] = {"A","B","D","H","I","E","J","M","N","C","F","G","K","L"};
String inOrder[] = {"H","D","I","B","E","M","J","N","A","F","C","K","G","L"};
- 问题2解决方案:我仔细分析了下,首先应该看先序,找到先序中的根节点,然后通过根节点确定在中序的位置,从而找到整体的左子树和右子树,例如上面这两个序列,可以先找到root A ,再确定A在inOrder中的位置,立刻就可以看出A左边的序列都是左子树,右边的序列是右子树;然后传左子树到Creat方法中,再利用递归,一个一个叉的建立起来,最后形成后序。
creat方法:
public Node creat(String []preOrder,int pstart,int pend,String []inOrder ,int instart,int inend){
if(pstart > pend || instart > inend){
return null;
}
String rootData = preOrder[pstart];
Node root = new Node(rootData);
int rootIndex = findIndexInArray(inOrder,rootData,instart,inend);
int xiabiao = rootIndex - instart - 1;
//左
Node left = creat(preOrder,pstart+1,pstart+xiabiao+1,inOrder,instart,instart+xiabiao);
//右
Node right = creat(preOrder,pstart + xiabiao + 2,pend,inOrder,rootIndex+1,inend);
root.setLeft(left);
root.setright(right);
return root;
}

-
问题3:在二叉排序树实现的时候,Delete方法我不太会用,尤其是删除有两个子树的节点,难倒我了。
-
问题3解决方案:在这篇博客中,介绍的很详细:JAVA实现二叉排序树(创建、中序遍历、插入节点和删除节点操作)
具体删除的过程是:
当删除叶子节点时,直接让他的父节点指向null就行,
当删除有一个子树的节点时,将其父节点指向其孩子节点。
当删除有两个孩子的节点时,先进行中序排列,按照排列出来的结果,将被删除的节点两边即视为为可代替原节点的备选节点,可以选择两者中的一个。将要被删除的节点数据删除,然后将代替节点的数据填入,之后再删除代替节点,若代替节点出现三种情况之一,即循环往复,直到全部删除。
具体的代码实现为:
public boolean delete(int key) // 删除结点
{
Node current = root;
Node parent = new Node();
boolean isRightChild = true;
while (current.data != key)
{
parent = current;
if (key > current.data)
{
current = current.right;
isRightChild = true;
}
else
{
current = current.left;
isRightChild = false;
}
if (current == null) return false; // 没有找到要删除的结点
}
// 此时current就是要删除的结点,parent为其父结点
// 要删除结点为叶子结点
if (current.right == null && current.left == null)
{
if (current == root)
{
root = null; // 整棵树清空
}
else
{
if (isRightChild)
parent.right = null;
else
parent.left = null;
}
return true;
}
//要删除结点有一个子结点
else if(current.left==null)
{
if(current==root)
root=current.right;
else if(isRightChild)
parent.right=current.right;
else
parent.left=current.right;
return true;
}
else if(current.right==null)
{
if(current==root)
root=current.left;
else if(isRightChild)
parent.right=current.left;
else
parent.left=current.left;
return true;
}
//要删除结点有两个子结点
else
{
Node successor=getSuccessor(current); //找到要删除结点的后继结点
if(current==root)
root=successor;
else if(isRightChild)
parent.right=successor;
else
parent.left=successor;
successor.left=current.left;
return true;
}
}
代码托管

上周考试错题总结
- [x] 第一题: It is possible to implement a stack and a queue in such a way that all operations take a constant amount of time.
- A .true
- B .false
解析:堆栈和队列的理想实现具有所有操作,这些操作都需要一定的时间。
故答案选 A
- [x] 第二题:To maintain the completeness of the tree, there is only one valid element to replace the root, and that is the element stored in the first leaf in the tree.
- A .true
- B .false
解析:为了保持树的完整性,只有一个有效的元素可以替换这个元素,那就是存储在树的最后一个叶子中的元素。
故答案选 B
点评过的同学博客和代码
其他(感悟、思考等)
已经打到10000行了,还有一个月,争取再干5000行。在这一学期的学习中,基本把所有学习的时间都给了java,但是很充实,也很 痛苦,但并快乐着。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 212/212 | 2/2 | 17/17 | |
| 第二周 | 132/344 | 2/4 | 17/34 | |
| 第三周 | 689/1033 | 1/5 | 23/67 | |
| 第四周 | 664/1697 | 2/7 | 20/87 | |
| 第五周 | 586/2283 | 2/9 | 20/107 | |
| 第六周 | 500/2783 | 1/10 | 26/133 | |
| 第七周 | 2143 /4928 | 2/12 | 40/173 | |
| 第八周 | 2000 /6140 | 2/14 | 40/210 | |
| 第九周 | 4000 /10140 | 3/17 | 40/250 |
-
计划学习时间:29小时
-
实际学习时间:40小时
-
改进情况:不妥协,死磕到底!
