大致题意:
给出一个点集,其中有一个点有相同的几率会被删除,求删除之后的点集够成的凸包上的点的平均数。
首先看到题目,可以考虑枚举删除的点,将其凸包上前后两点以及两点间凸包内所有点构建凸包,因为凸包内每个点
最多被访问一次,所以是O(N)的复杂度。理论上可行,但是实际上实现起来相当困难,又兴趣的可以去尝试。
这题的正解是先将所有的点求个凸包,若凸包顶点为偶数,则只需先删除凸包上的所有奇数点,然后求得一个凸包,然
后再删除凸包上偶数点,在求一次凸包,最后答案为
ans=两个凸包的顶点数+(m-1)*m-构建前两个凸包时经过的凸包的点数+删除的点在凸包内部的情况
奇数点同理,但要多计算一次。
附图 偶数点时
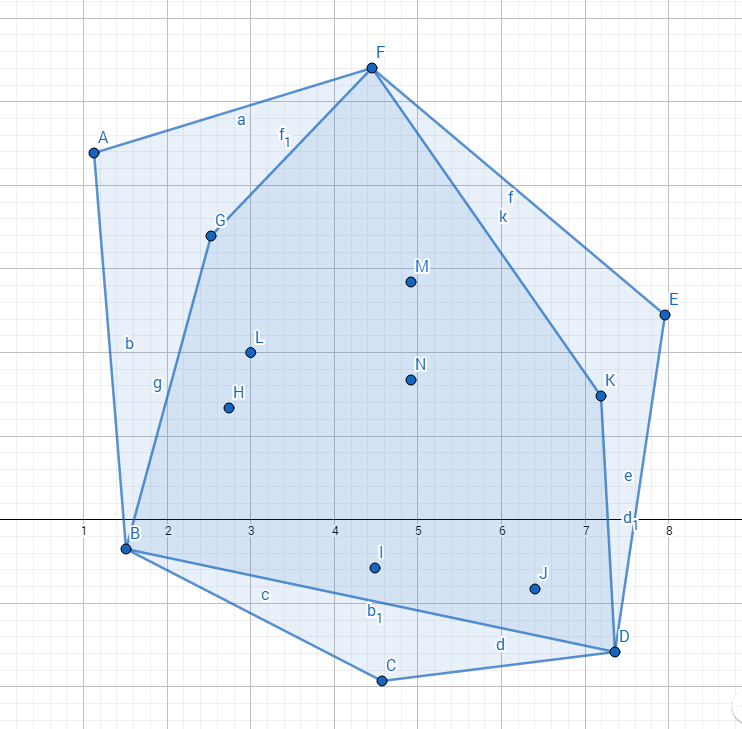
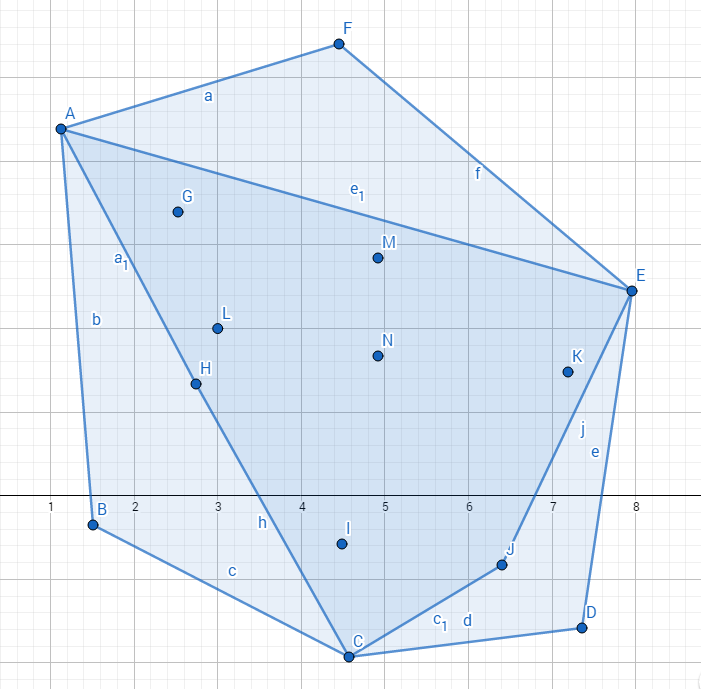
奇数点时
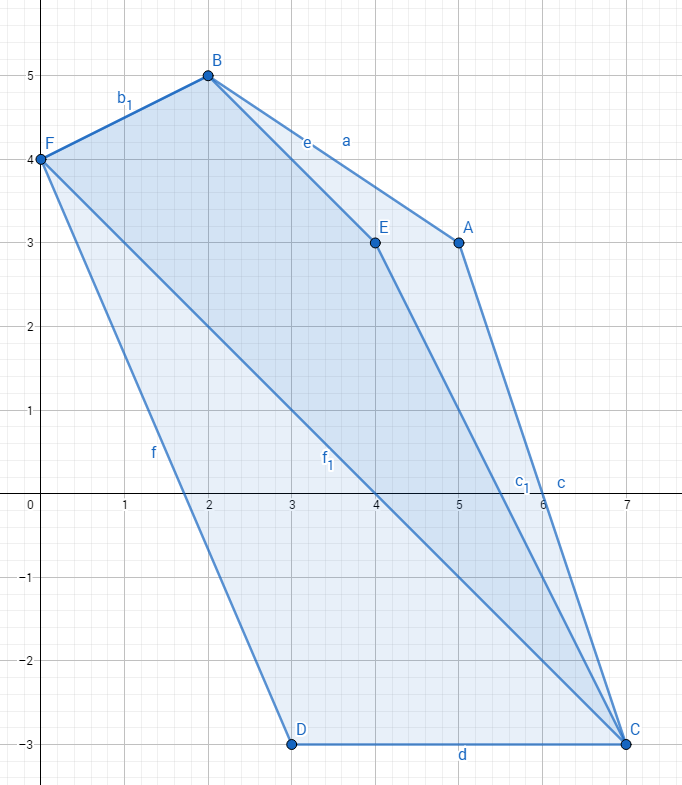
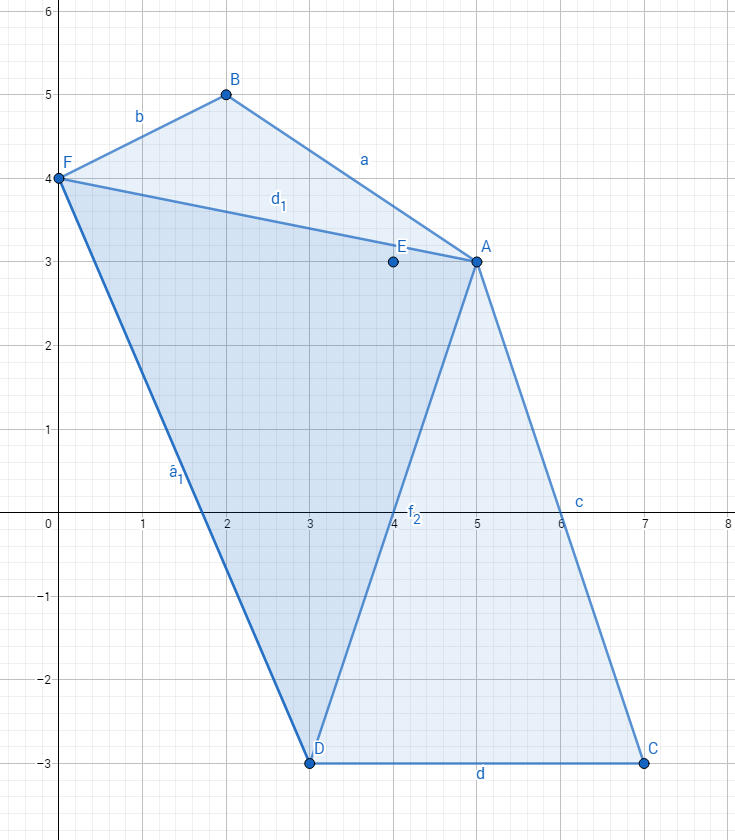

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #include<set> 7 #include<map> 8 #include<stack> 9 #include<time.h> 10 #include<cstdlib> 11 #include<cmath> 12 #include<list> 13 using namespace std; 14 #define MAXN 200100 15 #define eps 1e-5 16 #define For(i,a,b) for(int i=a;i<=b;i++) 17 #define Fore(i,a,b) for(int i=a;i>=b;i--) 18 #define lson l,mid,rt<<1 19 #define rson mid+1,r,rt<<1|1 20 #define mkp make_pair 21 #define pb push_back 22 #define cr clear() 23 #define sz size() 24 #define met(a,b) memset(a,b,sizeof(a)) 25 #define iossy ios::sync_with_stdio(false) 26 #define fre freopen 27 #define pi acos(-1.0) 28 #define inf 1e9+9 29 #define Vector Point 30 const int Mod=1e9+7; 31 typedef unsigned long long ull; 32 typedef long long ll; 33 typedef pair<int,int> pii; 34 typedef pair<ll,ll> pll; 35 int dcmp(double x){ 36 if(fabs(x)<=eps) return 0; 37 return x<0?-1:1; 38 } 39 struct Point { 40 double x,y; 41 int id; 42 int pre,nxt; 43 Point(double x=0,double y=0) : x(x),y(y) {} 44 Point operator - (const Point &a)const{ return Point(x-a.x,y-a.y); } 45 Point operator + (const Point &a)const{ return Point(x+a.x,y+a.y); } 46 Point operator * (const double &a)const{ return Point(x*a,y*a); } 47 Point operator / (const double &a)const{ return Point(x/a,y/a); } 48 bool operator < (const Point &a)const{ if(x==a.x) return y<a.y;return x<a.x; } 49 bool operator == (const Point &a)const{ return dcmp(x-a.x)==0 && dcmp(y-a.y)==0; } 50 void read(int iid=0) { scanf("%lf%lf",&x,&y);id=iid; } 51 void out(){cout<<"Bug: "<<x<<" "<<y<<endl;} 52 }; 53 inline double Cross(Vector a,Vector b) { return a.x*b.y-a.y*b.x; } 54 inline double Dot(Vector a,Vector b) { return a.x*b.x+a.y*b.y; } 55 inline double dis(Vector a) { return sqrt(Dot(a,a)); } 56 int ConvexHull(Point *p,int n,Point *ch){ 57 int m=0; 58 sort(p,p+n); 59 For(i,0,n-1){ 60 p[i].id=i; 61 while(m>1 && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--; 62 ch[m++]=p[i]; 63 } 64 int k=m; 65 Fore(i,n-2,0){ 66 while(m>k && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--; 67 ch[m++]=p[i]; 68 } 69 if(n>1) m--; 70 return m; 71 } 72 inline bool Onsegment(Point a,Point b1,Point b2){ 73 return dcmp(Cross(b1-a,b2-a))==0 && dcmp(Dot(b1-a,b2-a))<0; 74 } 75 bool Intersect_Segm_Segm(Point a1,Point a2,Point b1,Point b2){ 76 if(a1==b1 || a1==b2 || a2==b1 || a2==b2) return 1; 77 if(Onsegment(a1,b1,b2) || Onsegment(a2,b1,b2)) return 1; 78 double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1); 79 double c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1); 80 return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0; 81 } 82 Point Intersect_Line_Point(Point p,Vector u,Point q,Vector v){ 83 Vector w=p-q; 84 double t=Cross(v,w)/Cross(u,v); 85 return p+u*t; 86 } 87 int vis[MAXN],vvis[MAXN]; 88 int tcnt; 89 int tConvexHull(Point *p,int n,Point *ch){ 90 int m=0; 91 sort(p,p+n); 92 For(i,0,n-1){ 93 if(vis[p[i].id]) continue; 94 while(m>1 && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--; 95 ch[m++]=p[i]; 96 } 97 int k=m; 98 Fore(i,n-2,0){ 99 if(vis[p[i].id]) continue; 100 while(m>k && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--; 101 ch[m++]=p[i]; 102 } 103 if(ch[0]==ch[m-1]) m--; 104 For(i,0,m-1){ 105 if(vvis[ch[i].id]) tcnt++; 106 } 107 return m; 108 } 109 ll n; 110 Point ch[MAXN],p[MAXN],stk[MAXN]; 111 int solve(){ 112 scanf("%lld",&n); 113 tcnt=0; 114 met(vis,0); 115 met(vvis,0); 116 For(i,0,n-1) p[i].read(i); 117 int m=ConvexHull(p,n,ch); 118 For(i,0,m-1) vvis[ch[i].id]=1; 119 if(n==1) return puts("0/1"); 120 ll ans=m*1LL*(n-m); 121 if(m%2==0){ 122 For(i,0,m-1){ 123 vis[ch[i].id]=1; 124 i++; 125 } 126 ans+=tConvexHull(p,n,stk); 127 met(vis,0); 128 For(i,1,m-1){ 129 vis[ch[i].id]=1; 130 i++; 131 } 132 ans+=tConvexHull(p,n,stk); 133 }else{ 134 For(i,2,m-1){ 135 vis[ch[i].id]=1; 136 i++; 137 } 138 ans+=tConvexHull(p,n,stk); 139 met(vis,0); 140 For(i,1,m-1){ 141 vis[ch[i].id]=1; 142 i++; 143 } 144 ans+=tConvexHull(p,n,stk); 145 met(vis,0); 146 vis[ch[0].id]=1; 147 ans+=tConvexHull(p,n,stk); 148 } 149 ans+=m*1LL*(m-1)-tcnt; 150 ll cnt=__gcd(ans,n); 151 ans/=cnt; 152 n/=cnt; 153 printf("%lld/%lld ",ans,n); 154 } 155 int main(){ 156 // fre("in.txt","r",stdin); 157 fre("average.in","r",stdin); 158 fre("average.out","w",stdout); 159 int t=1; 160 solve(); 161 return 0; 162 }
