EZ 2018 06 24 NOIP2018 模拟赛（二十）

很久之前写的一套题了，由于今天的时间太多了，所以记起来就写掉算了。

这一场尽管T2写炸了，但也莫名Rank4涨了Rating。不过还是自己太菜。

A. 环游世界

首先我们先排个序，想一下如果不用走回来那么直接相邻的两个直接走就可以了。

那么我们要走回来呢，很简单，手动为回来留一条路径即可。还是一样的贪心方法，这次我们一般间隔两个。为什么是一般呢，其实也是对于边界的不同讨论了。

比如对于这样的一种情况，我们可以这样走：

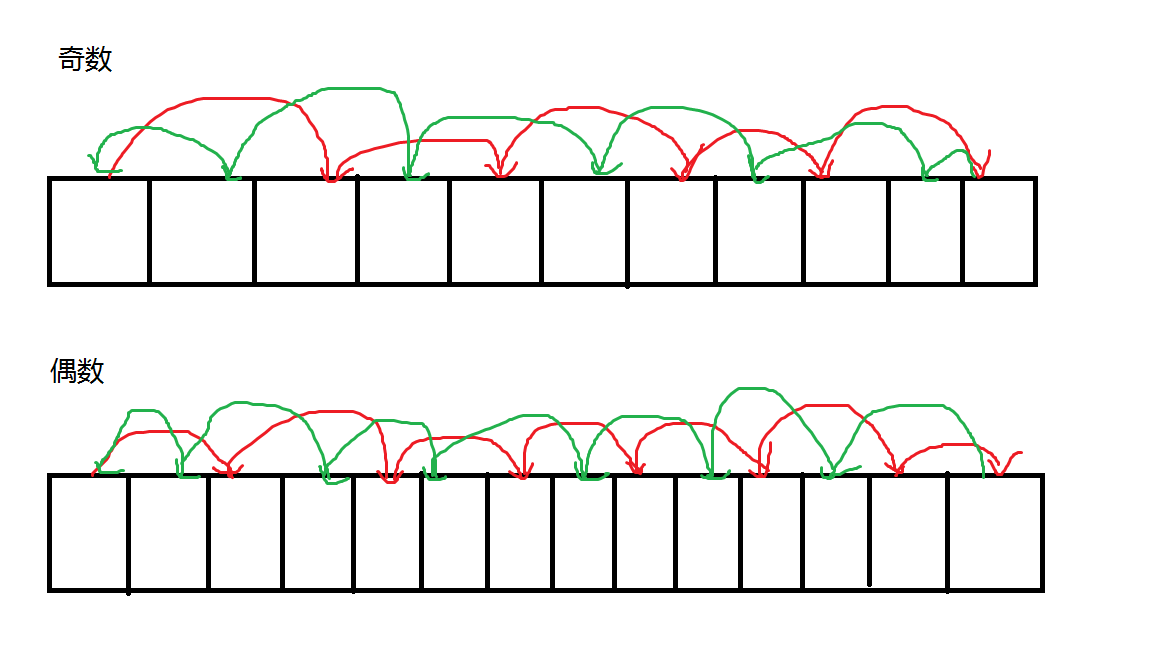
其中红色表示走过去的边，绿色表示走回来的边。

CODE

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e5+5;
int w[N],n;
long long ans;
inline char tc(void)
{
	static char fl[100000],*A=fl,*B=fl;
	return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
	x=0; char ch=tc();
	while (ch<'0'||ch>'9') ch=tc();
	while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc();
}
inline long long power(int x)
{
	return (long long)x*x*x;
}
inline void solve1(void)
{
	register int i;
	for (i=1;i+2<=n;i+=2)
	ans+=power(w[i+2]-w[i]);
	for (i=2;i+2<=n-1;i+=2)
	ans+=power(w[i+2]-w[i]);
	ans+=power(w[2]-w[1])+power(w[n]-w[n-1]);
	printf("%lld",ans);
}
inline void solve2(void)
{
	register int i;
	for (i=1;i+2<=n-1;i+=2)
	ans+=power(w[i+2]-w[i]);
	for (i=2;i+2<=n;i+=2)
	ans+=power(w[i+2]-w[i]);
	ans+=power(w[2]-w[1])+power(w[n]-w[n-1]);
	printf("%lld",ans);
}
int main()
{
	//freopen("A.in","r",stdin); freopen("A.out","w",stdout);
	register int i; read(n);
	for (i=1;i<=n;++i)
	read(w[i]); sort(w+1,w+n+1);
	if (n&1) solve1(); else solve2();
	return 0;
}

B. 献礼

一道比较显然的Dsu on tree（树上启发式合并）

题意大概就是在一个人的所有孩子中，找的所有开心的孩子中出现的颜色最多的一个。

如果最多的颜色的个数小于一个给定的值，那么这个人就会不开心。

其实像这种没有修改的题目写dsu还是很方便的。

记一下每个点出现颜色的最多的次数(mx)和颜色(mc)。然后还是先更新轻儿子，在算上重儿子并把轻儿子累加。还是一样的策略。

具体实现看CODE吧

#include<cstdio>
#include<cstring>
using namespace std;
const int N=2e5+5;
struct edge
{
	int to,next;
}e[N];
struct data
{
	int x,c;
}ans[N];
int head[N],s[N],id[N],size[N],son[N],t[N],col[N],w[N],cnt,tot,n,x,rt,mx,mc;
bool hap[N];
inline char tc(void)
{
	static char fl[100000],*A=fl,*B=fl;
	return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
	x=0; char ch=tc();
	while (ch<'0'||ch>'9') ch=tc();
	while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc();
}
inline void write(int x)
{
	if (x>9) write(x/10);
	putchar(x%10+'0');
}
inline void add(int x,int y)
{
	e[++cnt].to=y; e[cnt].next=head[x]; head[x]=cnt;
}
inline void DFS(int now)
{
	size[now]=1; id[now]=++tot; s[tot]=now; int res=-1;
	for (register int i=head[now];i!=-1;i=e[i].next)
	{
		DFS(e[i].to);
		size[now]+=size[e[i].to];
		if (size[e[i].to]>res) res=size[e[i].to],son[now]=e[i].to;
	}
}
inline void ins(int now)
{
	if (!hap[now]) return;
	if (++t[col[now]]>mx||(t[col[now]]==mx&&col[now]<mc)) mx=t[col[now]],mc=col[now];
}
inline void del(int now)
{
	t[col[now]]=0;
}
inline void dsu(int now)
{
	if (!son[now]) { if (!w[now]) hap[now]=1,ins(now); return; }
	register int i,j;
	for (i=head[now];i!=-1;i=e[i].next)
	if (e[i].to!=son[now])
	{
		dsu(e[i].to);
		for (j=id[e[i].to];j<=id[e[i].to]+size[e[i].to]-1;++j)
		del(s[j]); mx=mc=0;
	}
	if (son[now]) dsu(son[now]);
	for (i=head[now];i!=-1;i=e[i].next)
	if (e[i].to!=son[now])
	{
		for (j=id[e[i].to];j<=id[e[i].to]+size[e[i].to]-1;++j)
		ins(s[j]);
	}
	if (mx>=w[now])
	{
		ans[now].x=mx; ans[now].c=mc; 
		hap[now]=1; ins(now);
	}
}
int main()
{
	//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
	register int i; read(n);
	memset(head,-1,sizeof(head));
	memset(e,-1,sizeof(e));
	for (i=1;i<=n;++i)
	read(col[i]);
	for (i=1;i<=n;++i)
	{
		read(x); add(x,i);
		if (!x) rt=i;
	}
	for (i=1;i<=n;++i)
	read(w[i]);
	DFS(rt); dsu(rt);
	for (i=1;i<=n;++i)
	if (hap[i]) write(ans[i].x),putchar(' '),write(ans[i].c),putchar('
');
	else puts("oioi");
	return 0;
}

C. 幻想王国

作为一道斐波那契数列性质+矩阵快速幂的挺神仙的题目，还是有点超出范围了。

留着待坑吧