定理
-
(sum_{d|n}mu(d), n=1时为1,n > 1时为0)
-
设(F(i)=sum_{d|i}f(d))
形式一
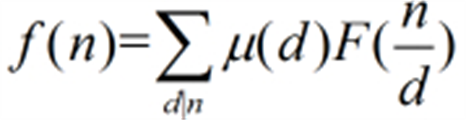
证明:(f(n)=sum_{d|n}mu(d)sum_{k|frac{n}{d}}f(k)=sum_{d|n}f(d)sum_{k|frac{n}{d}}mu(k))
(sum_{k|frac{n}{d}}mu(k)当1=frac{n}{d},即n=d时才为1,否则为0)
所以$f(n)=sum_{d|n}mu(d)F(frac {n}{d}) $
还有第二种形式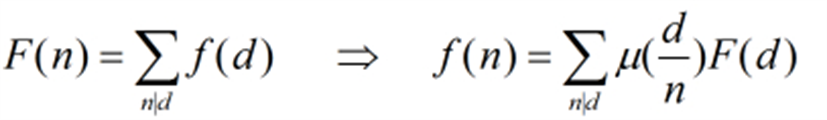
- $令 n = Pi_{p_i|n} p_{i} ^ {a_{i}} (
若m有)a_i>1(则)mu(i) = 0$
否则
若(a_i=1)有奇数个则(mu(i) = -1)
若(a_i=1)有偶数个则(mu(i) = 1)
不会证明找规律可证
有些大佬称之为容斥系数
求解u的代码,筛素数法
IL void Prime(){
isprime[1] = mu[1] = 1;
for(RG int i = 2; i < _; i++){
if(!isprime[i]) prime[++cnt] = i, mu[i] = -1;
for(RG int j = 1; j <= cnt && i * prime[j] < _; j++){
isprime[prime[j] * i] = 1;
if(!(i % prime[j])){ mu[i * prime[j]] = 0; break; }
else mu[prime[j] * i] = -mu[i];
}
}
}
应用
1
【HDU1695】GCD
求a<=x<=b,c<=y<=d,a<=x<=b,c<=y<=d
且gcd(x,y)=k的无序数对的个数
其中,你可以假定a=c=1a=c=1
所有数都<=100000<=100000
数据组数<=3000
。
。
。
即求(gcd(x, y)==1, x<=b/k, y<=d/k)的无序数对个数
设$f(i)为gcd(x, y) == i (的有序数对
)F(i) = ∑i|d f(d) (显然)F(i)表示gcd(x, y)==i$的倍数的有序数对
又显然 $F(i) = (b/k/i)*(d/k/i) $
然后用莫比乌斯反演求出 (f(i))
$f(1)=∑_{1|d} mu(d)F(d) $
因为是无序的,而我们求的是有序的,所以要去重
# include <bits/stdc++.h>
# define IL inline
# define RG register
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
const int _(100010);
IL ll Read(){
RG char c = getchar(); RG ll x = 0, z = 1;
for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
for(; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + c - '0';
return x * z;
}
int mu[_], prime[_], isprime[_], cnt;
IL void Prime(){
isprime[1] = mu[1] = 1;
for(RG int i = 2; i < _; i++){
if(!isprime[i]) prime[++cnt] = i, mu[i] = -1;
for(RG int j = 1; j <= cnt && i * prime[j] < _; j++){
isprime[prime[j] * i] = 1;
if(!(i % prime[j])){ mu[i * prime[j]] = 0; break; }
else mu[prime[j] * i] = -mu[i];
}
}
}
IL ll Calc(RG ll x, RG ll y){
RG ll ans = 0, _ans = 0, z = min(x, y);
for(RG ll i = 1; i <= z; i++) ans += mu[i] * (x / i) * (y / i);
for(RG ll i = 1; i <= z; i++) _ans += mu[i] * (z / i) * (z / i);
return ans - _ans / 2;
}
int main(RG int argc, RG char* argv[]){
Prime();
RG int n = Read(), x, y, d, Case = 0;
while(n--){
Read(), x = Read(), Read(), y = Read(), d = Read();
printf("Case %d: %lld
", ++Case, d ? Calc(x / d, y / d) : 0);
}
return 0;
}
2
[POI2007]ZAP-Queries
对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a,y<=b,并且gcd(x,y)=d
(1≤d≤a,b≤50 000) (1≤n≤50 000)
。
。
。
和上面的题目是一样的,只是这个是有序的,数据变大了直接蒯会TLE
因为(n/d)的个数只有根号个,所以,在某一段区间里面(n/i)是一样的,这时候我们用((n/(n/i)))优化去算就好了 预处理(mu(i))的前缀和)
那么我们可以把连续的一段d一起来算(分块):
设(a/d=x),那么最后一个(a/d=x即d=a/x),所以这段连续的区间就是([d,a/(a/d)])
# include <bits/stdc++.h>
# define IL inline
# define RG register
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
const int _(100010);
IL ll Read(){
RG char c = getchar(); RG ll x = 0, z = 1;
for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
for(; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + c - '0';
return x * z;
}
int mu[_], prime[_], isprime[_], cnt;
ll sum[_];
IL void Prime(){
isprime[1] = sum[1] = mu[1] = 1;
for(RG int i = 2; i < _; i++){
if(!isprime[i]) prime[++cnt] = i, mu[i] = -1;
for(RG int j = 1; j <= cnt && i * prime[j] < _; j++){
isprime[prime[j] * i] = 1;
if(!(i % prime[j])){ mu[i * prime[j]] = 0; break; }
else mu[prime[j] * i] = -mu[i];
}
}
for(RG int i = 2; i < _; i++) sum[i] = sum[i - 1] + mu[i];
}
IL ll Calc(RG ll x, RG ll y){
RG ll ans = 0, z = min(x, y);
for(RG ll i = 1, j; i <= z; i = j + 1){
j = min(x / (x / i), y / (y / i));
ans += (sum[j] - sum[i - 1]) * (x / i) * (y / i);
}
return ans;
}
int main(RG int argc, RG char* argv[]){
Prime();
RG int n = Read(), x, y, d;
while(n--){
x = Read(), y = Read(), d = Read();
printf("%lld
", d ? Calc(x / d, y / d) : 0);
}
return 0;
}
3
[HAOI2011]Problem b
对于给出的n个询问,每次求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y) = k,gcd(x,y)函数为x和y的最大公约数。
1≤n≤50000,1≤a≤b≤50000,1≤c≤d≤50000,1≤k≤50000
。
。
。
一样的再加上一个容斥即可
# include <bits/stdc++.h>
# define IL inline
# define RG register
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
const int _(100010);
IL ll Read(){
RG char c = getchar(); RG ll x = 0, z = 1;
for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
for(; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + c - '0';
return x * z;
}
int mu[_], prime[_], isprime[_], cnt;
ll sum[_];
IL void Prime(){
isprime[1] = sum[1] = mu[1] = 1;
for(RG int i = 2; i < _; i++){
if(!isprime[i]) prime[++cnt] = i, mu[i] = -1;
for(RG int j = 1; j <= cnt && i * prime[j] < _; j++){
isprime[prime[j] * i] = 1;
if(!(i % prime[j])){ mu[i * prime[j]] = 0; break; }
else mu[prime[j] * i] = -mu[i];
}
}
for(RG int i = 2; i < _; i++) sum[i] = sum[i - 1] + mu[i];
}
IL ll Calc(RG ll x, RG ll y){
RG ll ans = 0, z = min(x, y);
for(RG ll i = 1, j; i <= z; i = j + 1){
j = min(x / (x / i), y / (y / i));
ans += (sum[j] - sum[i - 1]) * (x / i) * (y / i);
}
return ans;
}
int main(RG int argc, RG char* argv[]){
Prime();
RG int n = Read(), a, b, c, d, k;
while(n--){
a = Read(), b = Read(), c = Read(), d = Read(), k = Read();
printf("%lld
", Calc(b / k, d / k) - Calc((a - 1) / k, d / k) - Calc((c - 1) / k, b / k) + Calc((a - 1) / k, (c - 1) / k));
}
return 0;
}
以上就是本蒟蒻的一些见解
题目可能比较水