图的遍历

1. 深度优先

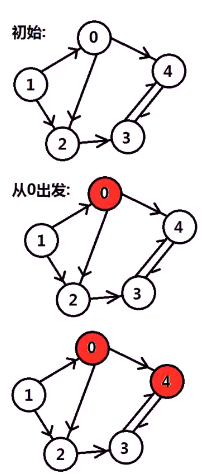
#include<iostream>
#include<vector>

using namespace std;

struct GrapNode {
    int label;
    vector<GrapNode*> neighbors;
    GrapNode(int x) : label(x) {};
};

void DFS_graph(GrapNode *node, int visit[]) {
    visit[node->label] = 1;        //标记已访问的顶点
    printf("%d ", node->label);
    for (int i = 0; i < node->neighbors.size(); i++) {
        if (visit[node->neighbors[i]->label] == 0) {    //访问相邻的且没有被访问的顶点
            DFS_graph(node->neighbors[i], visit);
        }
    }
}

int main() {
    const int MAX_N = 5;
    GrapNode *Graph[MAX_N];

    for (int i = 0; i < MAX_N; i++) {
        Graph[i] = new GrapNode(i);
    }

    Graph[0]->neighbors.push_back(Graph[4]);
    Graph[0]->neighbors.push_back(Graph[2]);
    Graph[1]->neighbors.push_back(Graph[0]);
    Graph[1]->neighbors.push_back(Graph[2]);
    Graph[2]->neighbors.push_back(Graph[3]);
    Graph[3]->neighbors.push_back(Graph[4]);
    Graph[4]->neighbors.push_back(Graph[3]);

    int visit[MAX_N] = { 0 };    //标记已被访问的顶点

    for (int i = 0; i < MAX_N; i++) {
        if (visit[i] == 0) {    //顶点没有被标记才会访问
            printf("From label(%d) : ", Graph[i]->label);
            DFS_graph(Graph[i], visit);
            printf("
");
        }
    }

    for (int i = 0; i < MAX_N; i++) {
        delete Graph[i];
    }

    return 0;
}

2.宽度优先

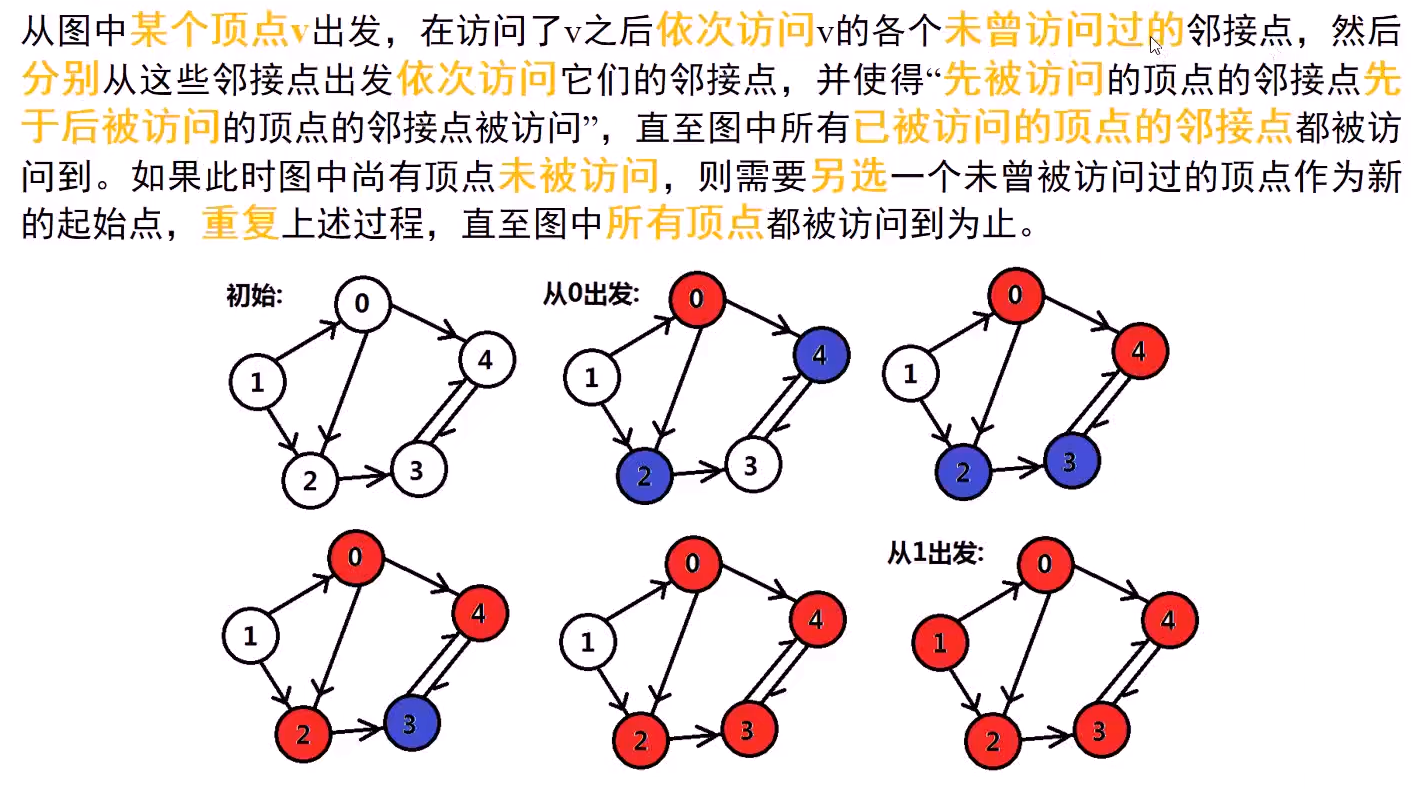
#include<iostream>
#include<vector>
#include<queue>

using namespace std;

struct GraphNode {
    int label;
    vector<GraphNode*> neighbors;
    GraphNode(int x) : label(x) {};
};

//宽度优先
void BFS_graph(GraphNode *node, int visit[]){
    queue<GraphNode*> Q;
    Q.push(node);
    visit[node->label] = 1;
    while (!Q.empty()) {
        GraphNode *node = Q.front();
        Q.pop();
        printf("%d ", node->label);
        for (int i = 0; i < node->neighbors.size(); i++) {
            if (visit[node->neighbors[i]->label] == 0) {
                Q.push(node->neighbors[i]);
                visit[node->neighbors[i]->label] = 1;
            }
        }
    }

}

int main() {
    const int MAX_N = 5;
    GraphNode *Graph[MAX_N];

    for (int i = 0; i < MAX_N; i++) {
        Graph[i] = new GraphNode(i);
    }

    Graph[0]->neighbors.push_back(Graph[4]);
    Graph[0]->neighbors.push_back(Graph[2]);
    Graph[1]->neighbors.push_back(Graph[0]);
    Graph[1]->neighbors.push_back(Graph[2]);
    Graph[2]->neighbors.push_back(Graph[3]);
    Graph[3]->neighbors.push_back(Graph[4]);
    Graph[4]->neighbors.push_back(Graph[3]);

    int visit[MAX_N] = { 0 };    //标记已被访问的顶点

    for (int i = 0; i < MAX_N; i++) {
        if (visit[i] == 0) {    //顶点没有被标记才会访问
            printf("From label(%d) : ", Graph[i]->label);
            BFS_graph(Graph[i], visit);
            printf("
");
        }
    }

    for (int i = 0; i < MAX_N; i++) {
        delete Graph[i];
    }

    return 0;
}

3. 判断有向图是否有环

（1）在深度优先搜索中，如果正在搜索某一个顶点（还未退出该顶点的递归深度搜索），又回到了该顶点，即证明有环。

（2）在宽度优先搜索时，只将入度为0的点添加至队列。当完成一个顶点的搜索（从队列中取出），它指向的所有顶点入度都减1，若此时某顶点入度为0则添加至队列，若完成宽度搜索后，所有的入度都为0，则图无环，否则有环。