(sroce : 100 + 100 + 10 + 12 + 24 + 40 = 286),还需继续加油鸭!
题解顺序按本人心中的难度顺序升序排序。
D1T1. 格雷码
题目链接:Link。
- 一道简单的分治。
- 1 位格雷码由两个 1 位二进制串组成,顺序为:0,1。
- (n + 1) 位格雷码的前 (2^n) 个二进制串,可以由依次算法生成的 (n) 位格雷码(总共 (2^n) 个 (n) 位二进制串)按顺序排列,再在每个串前加一个前缀 0 构成。
- (n + 1) 位格雷码的后 (2^n) 个二进制串,可以由依次算法生成的 (n) 位格雷码(总共 (2^n) 个 (n) 位二进制串)按逆序排列,再在每个串前加一个前缀 1 构成。
-
通过上面的这段 " 一种格雷码的生成算法 " 我们可以知道,对于任意的 (n(n geq 2)),(n) 位格雷码总是可以由 (n - 1) 位格雷码加一个前缀 0 或前缀 1 构成,考虑分治。
-
记 (calc(n, k)) 表示 (n) 位格雷码中的 (k) 号二进制串。
-
首先是递归边界 (n = 1),此时若 (k = 0),则 (calc(n, k) = 0);若 (k = 1),则 (calc(n, k) = 1)。
-
对于任意的 (n(n geq 2)),此时有两种情况:
- 若 (k < 2^{n - 1}),则 (calc(n, k) = 0 + calc(n - 1, k))。
- 若 (k geq 2^{n - 1}),则 (calc(n, k) = 1 + calc(n - 1, 2^n - 1 - k))。
-
时间复杂度 (mathcal{O(n)})。
-
记得开
unsigned long long! -
题外话。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
using namespace std;
int n;
unsigned long long k;
string calc(int n, unsigned long long k) {
if (n == 1) return k == 0 ? "0" : "1";
else {
unsigned long long S = 1ull << (n - 1);
if (k < S) return "0" + calc(n - 1, k);
else return "1" + calc(n - 1, 2 * S - 1 - k);
}
}
int main() {
cin >> n >> k;
cout << calc(n, k) << endl;
return 0;
}
D1T2. 括号树
题目链接:Link。
-
注意到答案的形式是 ((1 imes k_1) ext{xor} (2 imes k_2) ext{xor} (3 imes k_3) ext{xor} ⋯ ext{xor} (n imes k_n)),这使得我们难以对答案进行一些分析,只能乖乖地把 (k_1, k_2, k_3, ..., k_n) 都求出来,再计算出答案。
-
为了方便叙述,约定变量:
- (fa_x):(x) 号节点在树上的父亲编号。
- (lst_x):在 (1 sim x) 的路径中,能成功与 (x) 号节点上的括号匹配的深度最大的节点,当不存在能成功与 (x) 号节点上的括号匹配的节点时,(lst_x = -1)。
- (cnt_x):在 (1 sim x) 的路径中,以 (x) 号节点为结尾最多能数出多少个连续的括号块,例如
()(())((()))就能数出 (3) 个连续的括号块。
-
考虑对树进行一次广度优先遍历,一开始只有 (1) 号节点。
-
每次从队头取出节点 (u),考虑 (u) 的每条出边 ((u, v)),考虑计算 (k_v)。
-
首先答案可以先继承,即我们可以让 (k_v = k_u),然后再考虑一下将节点 (v) 上的括号加进 (s_u) 时产生的贡献。
-
首先当节点 (v) 上的括号为
(时,不会产生贡献。 -
考虑当节点 (v) 上的括号为
)时产生的贡献,令 (p = u),我们考虑让 (p) 去暴力跳 (lst) 数组,来找出与节点 (v) 上的)匹配的(的位置:- 当 (lst_p = -1) 时,此时 (p) 不能继续跳了。
若节点 (p) 上的括号是(,则匹配成功,结束匹配。
否则匹配失败,令 (p = 0)。 - 当 (lst_p eq -1) 时,令 (p = fa_{lst_p})。
- 当 (p = 0) 时,表示匹配失败,结束匹配。
- 当 (lst_p = -1) 时,此时 (p) 不能继续跳了。
-
当 (p eq 0) 时,我们就找到了与节点 (v) 上的
)匹配的(的位置 (p)。 -
则 (lst_v = p),(cnt_v = cnt_{fa_p} + 1),而此时加入节点 (v) 上的括号对答案贡献也即为 (cnt_v) 了,因为以节点 (v) 为结尾的连续的括号块的每一个后缀,都是合法括号串,一共有 (cnt_v) 个后缀。
-
注意到在跳的过程中,每一个括号块只会被经过一次(要么匹配成功,并建立了一个跨度更大的括号块,要么匹配失败,跳的时候就不会再涉及到该括号块),故时间复杂度 (O(n))。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 500100;
int n;
char s[N];
int tot, head[N], ver[N], Next[N];
void add(int u, int v) {
ver[++ tot] = v; Next[tot] = head[u]; head[u] = tot;
}
int fa[N];
int lst[N];
int cnt[N];
long long k[N];
void bfs() {
queue<int> q;
q.push(1);
memset(lst, -1, sizeof(lst));
while (q.size()) {
int u = q.front(); q.pop();
for (int i = head[u]; i; i = Next[i]) {
int v = ver[i];
q.push(v);
k[v] = k[u];
if (s[v] == '(') continue;
int p = u;
while (p) {
if (lst[p] == -1) {
if (s[p] == ')') p = 0;
break;
}
else p = fa[lst[p]];
}
if (p) {
lst[v] = p;
cnt[v] = cnt[fa[p]] + 1;
k[v] += cnt[v];
}
}
}
}
int main() {
scanf("%d", &n);
scanf("%s", s + 1);
for (int i = 2; i <= n; i ++) {
scanf("%d", &fa[i]);
add(fa[i], i);
}
bfs();
long long ans = 0;
for (int i = 1; i <= n; i ++)
ans ^= k[i] * i;
printf("%lld
", ans);
return 0;
}`
D2T1. Emiya 家今天的饭
题目链接:Link。
- 在不考虑每种主要食材至多在一半的菜中被使用时,答案即为:
-
我们可以简单容斥一下,先求出在 " 存在一种主要食材使用次数大于菜的一半 " 情况下的方案数,再与上式做个差即可求出答案。
-
注意到有且仅有一种主要食材使用次数大于菜的一半,我们可以枚举这个主要食材,记我们枚举的主要食材的编号为 (col),对于每一个主要食材,考虑 dp。
-
设 (f_{i, j, k}) 表示:在前 (i) 个烹饪方法中,做了 (j) 道菜,且第 (col) 种主要食材用了 (k) 个时的方案数。
-
设 (S_i = sumlimits_{j = 1}^m a_{i, j}),根据题意,转移有三种:
-
不使用第 (i) 个烹饪方法做菜。此时可以从 " 在前 (i - 1) 个烹饪方法中,做了 (j) 道菜,且第 (col) 种主要食材用了 (k) 个 " 转移而来,故该种转移的方案数为 (f_{i - 1, j, k})。
-
使用第 (i) 个烹饪方法做菜,使用第 (col) 种主要食材。此时可以从 " 在前 (i - 1) 个烹饪方法中,做了 (j - 1) 道菜,且第 (col) 种主要食材用了 (k - 1) 个 " 转移而来,使用第 (i) 个烹饪方法且使用第 (j) 个主要食材可以制作出 (a_{i, col}) 道菜,根据乘法原理,该种转移的方案数为 (f_{i - 1, j - 1, k - 1} ast a_{i, col})。
-
使用第 (i) 个烹饪方法做菜,不使用第 (col) 种主要食材。此时可以从 " 在前 (i - 1) 个烹饪方法中,做了 (j - 1) 道菜,且第 (col) 种主要食材用了 (k) 个 " 转移而来,使用第 (i) 个烹饪方法且不使用第 (j) 个主要食材可以制作出 (S_i - a_{i, col}) 道菜,根据乘法原理,该种转移的方案数为 (f_{i - 1, j - 1, k} ast (S_i - a_{i, col}))。
-
-
故有状态转移方程:
- 初态:(f_{i, 0, 0} = 1)。
- 目标:(sumlimits_{j = 1}^nsumlimits_{k = leftlfloorfrac{j}{2} ight floor + 1}^j f_{n, j, k})。
- 直接做 dp 的时间复杂度 (mathcal{O(n^3 m)}),考虑进一步优化。
- 考虑维度合并,注意到我们只关心 (leftlfloorfrac{j}{2} ight floor) 与 (k) 的差值,并不关心 (j) 与 (k) 的值具体是多少,于是我们可以将 (j) 这一维和 (k) 这一维进行合并。
- 设 (f_{i, j}) 表示:在前 (i) 个烹饪方法中," 使用第 (col) 种主要食材做的菜数 " 减去 " 不使用第 (col) 种主要食材做的菜数 " 的差值为 (j) 时的方案数。
- 转移依旧是上述的三种。
- 简单分析即可得到状态转移方程:
- 初态:(f_{0, 0} = 1)。
- 目标:(sumlimits_{j = 1}^n f_{n, j})。
- 时间复杂度 (mathcal{O(n^2 m)})。
- 注意到差值 (j) 也有可能是负数,所以我们需要用一个偏移量 (base),使得值域变为非负整数域后再进行处理。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
inline int read() {
int x = 0, f = 1; char s = getchar();
while (s < '0' || s > '9') { if (s == '-') f = -f; s = getchar(); }
while (s >= '0' && s <= '9') { x = x * 10 + s - '0'; s = getchar(); }
return x * f;
}
const int N = 110, M = 2010, base = 100;
const int mod = 998244353;
int n, m;
int a[N][M];
int S[N];
int f[N][N * 2];
int main() {
n = read(), m = read();
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
a[i][j] = read();
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
S[i] = (S[i] + a[i][j]) % mod;
int ans = 1;
for (int i = 1; i <= n; i ++)
ans = 1ll * ans * (S[i] + 1) % mod;
ans = ((ans - 1) % mod + mod) % mod;
for (int col = 1; col <= m; col ++) {
memset(f, 0, sizeof(f));
f[0][0 + base] = 1;
for (int i = 1; i <= n; i ++)
for (int j = -i + base; j <= i + base; j ++) {
int val = 0;
val = (val + f[i - 1][j]) % mod;
if (j) val = (val + 1ll * f[i - 1][j - 1] * a[i][col]) % mod;
val = (val + 1ll * f[i - 1][j + 1] * (S[i] - a[i][col])) % mod;
val = (val % mod + mod) % mod;
f[i][j] = val;
}
for (int j = 1 + base; j <= n + base; j ++)
ans = ((ans - f[n][j]) % mod + mod) % mod;
}
printf("%d
", ans);
return 0;
}
D2T2. 划分
题目链接:Link。
- 考虑 dp,记 (S_i = sumlimits_{j = 1}^i a_j)。
- 设 (f_{i, j}) 表示:考虑到前 (i) 项,划分的最后一段区间为 ((j, i]) 时,能取得的最小的平方和。
- 显然有状态转移方程:
- 直接做的时间复杂度为 (mathcal{O(n^3)})。
- 有一个结论:定义决策点 (k) 若满足 (S_j - S_k leq S_i - S_j),则被称为 " 合法 ",对于合法的两个决策点 (k_1, k_2),不妨设 (k_1 < k_2),则决策点 (k_2) 不劣于 (k_1)。
证明略,但是看起来就比较显然对不对。- 我们可以得知 (f_{i, j}) 的最优决策点是 " 合法 " 的所有决策点中,位置最靠后的那个决策点。
- 也就是说,当最后若干段尽量小时,能取得的平方和会尽量小。
- 于是我们大力 dp。
- 约定变量:
- (f_i):考虑到前 (i) 项时,能取得的最小的平方和。
- (dec_i):(f_i) 的最优决策点。
- (suf_i):(f_i) 中最后一段划分的区间和,其实就是 (S_i - S_{dec_i})。
- 显然有状态转移方程:
- 我们重新定义:当决策点 (j) 若满足 (suf_j leq S_i - S_j) ,则被称为 " 合法 ",移项得 (suf_j + S_j leq S_i)。
- 考虑 (f_i) 的最优决策点 (dec_i),根据上述结论,我们知道最优决策点 (dec_i) 是 " 合法 " 的所有决策点中,位置最靠后的那个决策点,注意到 (suf_j + S_j leq S_i) 中的 (S_i) 是单调递增的,说明决策集合只增大不减小,我们可以用一个变量 (p) 表示处理到前 (i) 项时," 合法 " 的所有决策中,位置最靠后的那个。考虑单调队列维护决策,我们维护一个下标 (j) 递增,(suf_j + S_j) 也递增的单调队列。
- 令 (i = 1 sim n),对于每个 (i) 执行以下三个步骤。
- 判断队头决策 (j) 是否满足 (suf_j + S_j leq S_i)。若满足,则令 (p = max(p, j)),将队头出队。
- 此时 (p) 就是 (f_i) 的最优决策点 (dec_i)。
- 不断删除队尾决策 (j),直到决策 (j) 满足 (suf_j + S_i leq suf_j + S_j),然后把 (i) 作为一个新的决策入队。
- 注意到样例 3 输出 4972194419293431240859891640 ...
- 一看就是要打高精,时空复杂度都比较紧张,我们在转移的时候,并不用计算出 dp 值 (f_i),只需记录 (f_i) 的最优决策点 (dec_i) 即可,最后从 (n) 倒推回去并计算答案。
- 发现其实 (S, dec, suf) 数组都还可以开的下,而且 (suf) 也并不必要开数组存。
只是最后计算答案的时候需要用到高精。 - 时间复杂度 (mathcal{O(n)})。
- 我比较懒,用的
__int128,大家还是好好打高精吧(:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
inline int read() {
int x = 0, f = 1; char s = getchar();
while (s < '0' || s > '9') { if (s == '-') f = -f; s = getchar(); }
while (s >= '0' && s <= '9') { x = x * 10 + s - '0'; s = getchar(); }
return x * f;
}
inline void print(__int128 x) {
if (x > 9) print(x / 10);
putchar('0' + x % 10);
}
const int N = 40001000, M = 100100;
int n, type;
int a[N];
void makedata() {
static int x, y, z, b[N], m, p[M], l[M], r[M], mod = (1 << 30);
x = read(), y = read(), z = read(), b[1] = read(), b[2] = read(), m = read();
p[0] = 0;
for (int i = 1; i <= m; i ++)
p[i] = read(), l[i] = read(), r[i] = read();
for (int i = 3; i <= n; i ++)
b[i] = (1ll * x * b[i - 1] + 1ll * y * b[i - 2] + z) % mod;
for (int j = 1; j <= m; j ++)
for (int i = p[j - 1] + 1; i <= p[j]; i ++)
a[i] = (b[i] % (r[j] - l[j] + 1)) + l[j];
}
long long S[N];
int l, r;
int q[N];
int dec[N];
long long suf(int x) {
return S[x] - S[dec[x]];
}
int main() {
n = read(), type = read();
if (type == 1) makedata();
else
for (int i = 1; i <= n; i ++)
a[i] = read();
for (int i = 1; i <= n; i ++)
S[i] = S[i - 1] + a[i];
l = 1, r = 1;
q[1] = 0;
int p = 0;
for (int i = 1; i <= n; i ++) {
while (l <= r && S[q[l]] + suf(q[l]) <= S[i]) p = max(p, q[l ++]);
dec[i] = p;
while (l <= r && S[q[r]] + suf(q[r]) >= S[i] + suf(i)) r --;
q[++ r] = i;
}
__int128 ans = 0;
int x = n;
while (x) {
ans += (__int128) suf(x) * suf(x);
x = dec[x];
}
print(ans);
return 0;
}
D2T3. 树的重心
题目链接:Link。
部分分还是有一些细讲的价值的。
Test (1 sim 8)
特殊性质:(n leq 2000)。
-
暴力莽,暴力枚举每一条边的时间复杂度是 (mathcal{O(n)}),暴力求重心的时间复杂度是 (mathcal{O(n)})。
-
暴力求重心大家应该都会吧 ... -
时间复杂度 (mathcal{O(n^2)}),这档分还是要吃掉的。
Test (9 sim 11)
特殊性质:树的形态为一条链。
- 当树的形态为一条链的时候,显然该树的重心就是链的中间点,1 个或 2 个。
- 这时候,我们删掉一条边,树会被分解成两部分,每部分都是一条链,于是取这两部分的中间点计入答案即可。
- 具体的,设链上第 (i) 个节点的编号为 (p_i)。
- 令 (i = 1 sim n - 1),这时候我们要删掉 ((p_i, p_{i + 1})) 这条边。
考虑先求 (1 sim i) 部分的重心,对 (i) 的奇偶性讨论一下:- 当 (i) 是奇数时,(p_{frac{i + 1}{2}}) 是重心。
- 当 (i) 是偶数时,(p_{frac{i}{2}}) 和 (p_{frac{i}{2} + 1}) 是重心。
- 求 (i + 1 sim n) 部分的重心,翻转一下 (p) 再做一次即可。
- 时间复杂度 (mathcal{O(n)}),吃掉这档分还是比较简单的。
Test (12 sim 15)
特殊性质:树的形态为满二叉树。
- 当树的形态为满二叉树的时候,删掉一条边 ((u, v)),不妨设 (u) 是 (v) 的父亲。
- (v) 的子树内的重心还是很好分析的,显然 (v) 的子树也是满二叉树,故重心即为 (v)。
- 考虑在原树中刨去 (v) 的子树后,重心的分布。不妨设树的深度为 (d)。
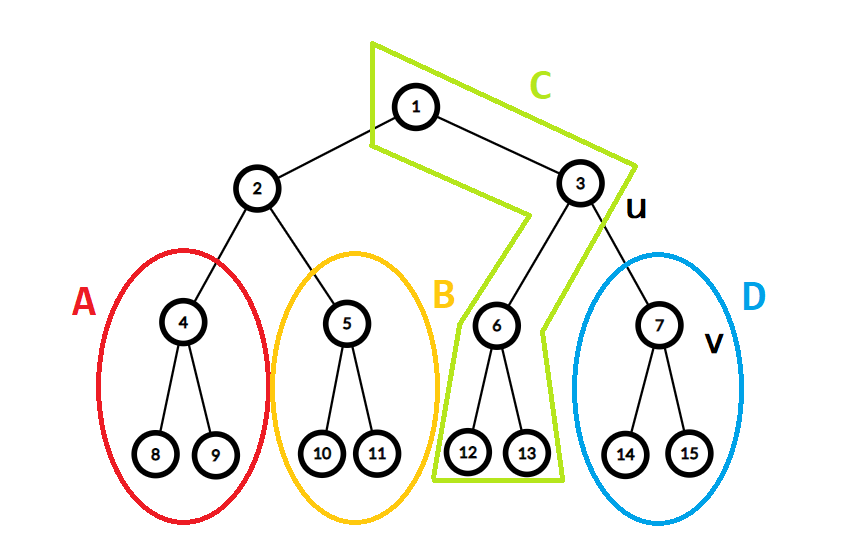
-
上图是一棵满二叉树,我们先对 ((u, v)) 在满二叉树的右侧时讨论,左侧同理。
我们把树分成了 四个部分 和 一个点,设 (v) 的深度为 (p),则各个部分的节点数为:- (color{red}A color{black}: 2^{d-2} - 1)。
- (color{yellow}B color{black}: 2^{d-2} - 1)。
- (color{green}C color{black}: 2^{d - 1} - 2^{d - p + 1} + 1)。
- (color{blue}D color{black}: 2^{d - p + 1} - 1)。
-
首先,重心显然不会出现在 (color{red}A) 和 (color{yellow}B) 里,也并不可能出现在 (color{green}C) 中除了根节点以外的节点中。
-
我们对 (2) 号点(根的其中一个儿子)与根节点进行重点讨论:
- 删除 (2) 号点后剩下的最大子树:(x = max(2^{d - 2} - 1, 2^{d - 1} - 2^{d - p + 1} + 1))。
- 删除根节点后剩下的最大子树:(y = max(2^{d - 1} - 1, 2^{d - 1} - 2^{d - p + 1}))。
-
当 (p < d) 时,有 (x < 2^{d - 1} - 1),(y = 2^{d - 1} - 1)。(x < y),此时 (2) 号点是重心。
-
当 (p = d) 时,有 (x = 2^{d - 1} - 1),(y = 2^{d - 1} - 1)。(x = y),此时 (2) 号点与根节点都是重心。
-
设根节点为 (a),根节点的左儿子为 (b),根节点的右儿子为 (c)。我们发现,当 ((u, v)) 在满二叉树的右侧时,这条边对答案有 (b) 的贡献,当 ((u, v)) 在满二叉树的左侧时,这条边对答案有 (c) 的贡献,特别地,当 ((u, v)) 中的 (v) 为叶节点时,这条边对答案还有额外的 (a) 的贡献。
-
经过上述分析,故答案为:
Solution
-
不难想到,可以对于每个点 (u),计算 (u) 成为重心时,对答案的贡献。
-
我们钦定点 (u) 为整棵树的根,现在有一个 (u) 的子节点 (v),我们要从 (v) 的子树中再删去一个大小为 (x) 的小子树,使得 (u) 成为重心。
-
约定变量:
-
(size_v):以 (u) 为根时,(v) 的子树大小。
-
(size'_v):经过删边后的 (v) 的子树大小,这里实际上 (size'_v = size_v - x)。
-
(s):在 (u) 的所有子树中,刨去 (v) 的子树后的总节点数,这里实际上 (s = n - 1 - size_v)。
-
(m):在 (u) 的所有子树中,除 (v) 之外的最大子树大小。
-
-
我们来分析一下,经过删边后的 (size'_v) 的取值范围:
- (1)(v) 的子树大小不能比 (u) 的其他子树大小的和加 (1) 还要大,否则重心取 (v) 会更加平衡。则有:
[size_v' leq s + 1 ]- (2)除 (v) 之外的最大子树大小不能比 (u) 其他子树大小的和加 (1) 还要大,否则重心取最大子树的根会更加平衡。则有:
[m leq s - m + size'_v + 1 ] -
经过上述分析,我们可以知道,经过删边后的 (size'_v in [2 ast m - s - 1, s + 1])。
- 于是问题转化为 (v) 的子树内有多少个点的子树大小在某个区间范围内,线段树合并直接可以 rush 掉。
- 显然不能每次都以 (u) 为根重新做一遍线段树合并,我们钦定 (1) 为整棵树的根。
- 对于 (v) 是 (u) 的子节点,我们可以线段树合并简单统计一下。
对于 (v) 是 (u) 的父亲节点时,我们再讨论一下边的分布。 - 设 (l = 2 ast (n - size_u) - n),(r = n - 2 ast m)。
- 对于 (1 sim u) 的路径中的边 ((a, b)),不妨设 (a) 是 (b) 的父亲,当删去 ((a, b)) 这条边时,包含 (a) 的这一块的子树大小为 (n - size_b),反过来我们可以得到,删去 ((a, b)) 这条边会使得 (u) 成为重心当且仅当 (size_b in [n - r, n - l])。
- 对于非 (1 sim u) 的路径中的边 ((a, b)),我们可以简单容斥一下,该类型边的边数即为: " 整棵树中子树大小在 ([l, r]) 内的点的个数 " 减去 " (u) 的子树中子树大小在 ([l, r]) 内的点的个数 " 减去 " (1 sim u) 的路径中子树大小在 ([l, r]) 内的点的个数 "。
- 结合上述两种情况,我们可以得知,当 (v) 是 (u) 的父亲节点时,满足删去 ((a, b)) 后会使得 (u) 成为重心的边数为:" 整棵树中子树大小在 ([l, r]) 内的点的个数 " 减去 " (u) 的子树中子树大小在 ([l, r]) 内的点的个数 " 减去 " (1 sim u) 的路径中子树大小在 ([l, r]) 内的点的个数 " 加上 " (1 sim u) 的路径中子树大小在 ([n - r, n - l]) 内的点的个数 "。
-
对于整棵树的区间数点问题,我们可以预处理出前缀和 (sum_i) 表示 " 在整棵树中,子树大小在 ([1, i]) 内的节点个数 ",从而转化为前缀做差的形式。
-
对于子树内的区间数点问题,我们可以用顺手处理的线段树合并计算。
-
对于根节点到 (u) 点路径上的区间数点问题,我们可以用一个树状数组实时维护根节点到 (u) 点的子树大小,还是可以用前缀做差的形式计算。
- 时间复杂度 (mathcal{O(n log n)}),空间复杂度 (mathcal{O(n log n)})。
但是好像常数有点大。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
inline int read() {
int x = 0, f = 1; char s = getchar();
while (s < '0' || s > '9') { if (s == '-') f = -f; s = getchar(); }
while (s >= '0' && s <= '9') { x = x * 10 + s - '0'; s = getchar(); }
return x * f;
}
const int N = 300100, M = 600100, MLOGN = 10000000;
int n;
int ovo, head[N], ver[M], Next[M];
void addedge(int u, int v) {
ver[++ ovo] = v; Next[ovo] = head[u]; head[u] = ovo;
}
// BIT part
int c[N];
void add(int x, int val) {
for (; x <= n; x += x & -x) c[x] += val;
}
int calc(int x) {
int ans = 0;
for (; x; x -= x & -x) ans += c[x];
return ans;
}
// SegmentTree part
int tot, root[N];
struct SegmentTree {
int lc, rc;
int cnt;
} t[MLOGN];
int New() {
tot ++;
t[tot].lc = t[tot].rc = t[tot].cnt = 0;
return tot;
}
void insert(int &p, int l, int r, int delta, int val) {
if (!p) p = New();
t[p].cnt += val;
if (l == r) return;
int mid = (l + r) / 2;
if (delta <= mid)
insert(t[p].lc, l, mid, delta, val);
else
insert(t[p].rc, mid + 1, r, delta, val);
}
int merge(int p, int q) {
if (!p || !q)
return p ^ q;
t[p].cnt += t[q].cnt;
t[p].lc = merge(t[p].lc, t[q].lc);
t[p].rc = merge(t[p].rc, t[q].rc);
return p;
}
int ask(int p, int l, int r, int s, int e) {
if (s <= l && r <= e)
return t[p].cnt;
int mid = (l + r) / 2;
int val = 0;
if (s <= mid)
val += ask(t[p].lc, l, mid, s, e);
if (mid < e)
val += ask(t[p].rc, mid + 1, r, s, e);
return val;
}
// solve part
long long ans;
int size[N];
void search(int u, int fa) {
size[u] = 1;
for (int i = head[u]; i; i = Next[i]) {
int v = ver[i];
if (v == fa) continue;
search(v, u);
size[u] += size[v];
}
}
long long sum[N];
void dfs(int u, int fa) {
int firv = 0, secv = 0;
for (int i = head[u]; i; i = Next[i]) {
int v = ver[i];
if (v == fa) continue;
if (size[v] > firv) secv = firv, firv = size[v];
else if (size[v] > secv) secv = size[v];
}
if (n - size[u] > firv) secv = firv, firv = n - size[u];
else if (n - size[u] > secv) secv = n - size[u];
for (int i = head[u]; i; i = Next[i]) {
int v = ver[i];
if (v == fa) continue;
add(size[v], 1), dfs(v, u), add(size[v], -1);
int m = size[v] == firv ? secv : firv;
int l = 2 * size[v] - n, r = n - 2 * m;
if (l > n || r < 1 || l > r) {
root[u] = merge(root[u], root[v]);
continue;
}
if (l < 1) l = 1;
if (r > n) r = n;
ans += 1ll * ask(root[v], 1, n, l, r) * u;
root[u] = merge(root[u], root[v]);
}
if (u == 1)
return;
int m = n - size[u] == firv ? secv : firv;
int l = 2 * (n - size[u]) - n, r = n - 2 * m;
if (l > n || r < 1 || l > r) {
insert(root[u], 1, n, size[u], 1);
return;
}
if (l < 1) l = 1;
if (r > n) r = n;
int cnt = 0;
cnt += sum[r] - sum[l - 1];
cnt -= ask(root[u], 1, n, l, r);
cnt -= calc(r) - calc(l - 1);
l = n - l, r = n - r, swap(l, r);
if (l < 1) l = 1;
if (r > n) r = n;
cnt += calc(r) - calc(l - 1);
ans += 1ll * cnt * u;
insert(root[u], 1, n, size[u], 1);
}
void work() {
memset(head, 0, sizeof(head));
memset(c, 0, sizeof(c));
memset(sum, 0, sizeof(sum));
memset(root, 0, sizeof(root));
ovo = 0, tot = 0, ans = 0;
n = read();
for (int i = 1; i < n; i ++) {
int u = read(), v = read();
addedge(u, v), addedge(v, u);
}
search(1, 0);
for (int i = 2; i <= n; i ++)
sum[size[i]] ++;
for (int i = 2; i <= n; i ++)
sum[i] += sum[i - 1];
dfs(1, 0);
printf("%lld
", ans);
}
int main() {
int T = read();
while (T --) work();
return 0;
}
D1T3. 树上的数
题目链接:Link。
咕咕咕。
我是不会告诉您其实我不会做这道题的 233。