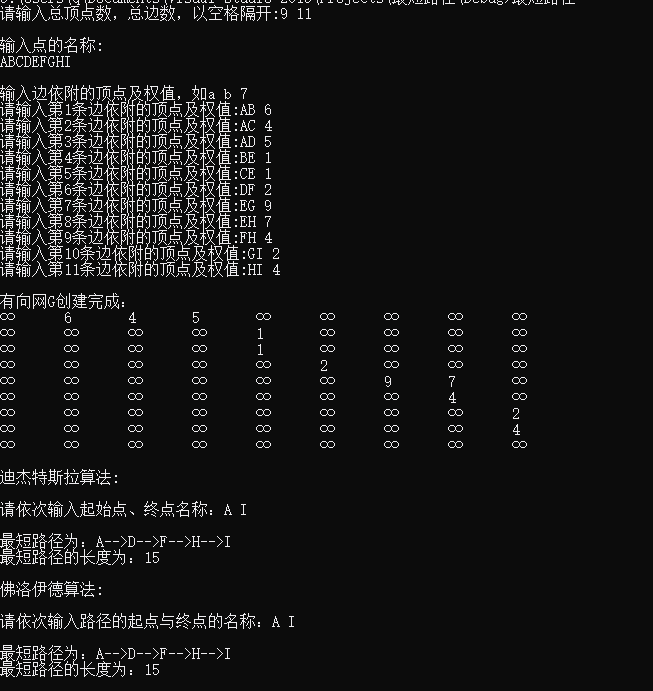
有向图找最短路径
/*最短路径*/ #include <iostream> using namespace std; #define MaxInt 32767 //表示极大值,即∞ #define MVNum 100 //最大顶点数 typedef char VerTexType; //假设顶点的数据类型为字符型 typedef int ArcType; //假设边的权值类型为整型 typedef struct { VerTexType vexs[MVNum]; //顶点表 ArcType arcs[MVNum][MVNum]; //邻接矩阵 int vexnum, arcnum; //图的当前点数和边数 }AMGraph; int LocateVex(AMGraph G, VerTexType v) { for (int i = 0; i < G.vexnum; ++i) if (G.vexs[i] == v) return i; return -1; } void CreateUDN(AMGraph &G) { int i, j, k; cout << "请输入总顶点数,总边数,以空格隔开:"; cin >> G.vexnum >> G.arcnum; cout << endl; cout << "输入点的名称:" << endl; for (i = 0; i < G.vexnum; ++i) { cin >> G.vexs[i]; } cout << endl; for (i = 0; i < G.vexnum; ++i) for (j = 0; j < G.vexnum; ++j) G.arcs[i][j] = MaxInt; cout << "输入边依附的顶点及权值,如a b 7" << endl; for (k = 0; k < G.arcnum; ++k) { VerTexType v1, v2; ArcType w; cout << "请输入第" << (k + 1) << "条边依附的顶点及权值:"; cin >> v1 >> v2 >> w; i = LocateVex(G, v1); j = LocateVex(G, v2); G.arcs[i][j] = w; } } /***************迪杰特斯拉算法****************/ int *D = new int[MVNum]; //用于记录最短路的长度 bool *S = new bool[MVNum]; //标记顶点是否进入S集合 int *Path = new int[MVNum]; //用于记录最短路顶点的前驱 void ShortestPath_DIJ(AMGraph G, int v0) { //用Dijkstra算法求有向网G的v0顶点到其余顶点的最短路径 int v, i, w, min; int n = G.vexnum; //n为G中顶点的个数 for (v = 0; v < n; ++v) { //n个顶点依次初始化 S[v] = false; //S初始为空集 D[v] = G.arcs[v0][v]; //将v0到各个终点的最短路径长度初始化为弧上的权值 if (D[v] < MaxInt) Path[v] = v0; //如果v0和v之间有弧,则将v的前驱置为v0 else Path[v] = -1; //如果v0和v之间无弧,则将v的前驱置为-1 }//for S[v0] = true; //将v0加入S D[v0] = 0; //源点到源点的距离为0 for (i = 1; i < n; ++i) { //对其余n-1个顶点,依次进行计算 min = MaxInt; for (w = 0; w < n; ++w) if (!S[w] && D[w] < min) { //选择一条当前的最短路径,终点为v v = w; min = D[w]; } S[v] = true; //将v加入S for (w = 0; w < n; ++w) //更新从v0出发到集合V?S上所有顶点的最短路径长度 if (!S[w] && (D[v] + G.arcs[v][w] < D[w])) { D[w] = D[v] + G.arcs[v][w]; //更新D[w] Path[w] = v; //更改w的前驱为v } } } void DisplayPath_DIJ(AMGraph G, int begin, int temp) { if (Path[temp] != -1) { DisplayPath_DIJ(G, begin, Path[temp]); cout << G.vexs[Path[temp]] << "-->"; } } /***************佛洛伊德算法*************/ int Path_F[MVNum][MVNum]; //最短路径上顶点vj的前一顶点的序号 int D_F[MVNum][MVNum]; //记录顶点vi和vj之间的最短路径长度 void ShortestPath_Floyed(AMGraph G) { //用Floyd算法求有向网G中各对顶点i和j之间的最短路径 int i, j, k; for (i = 0; i < G.vexnum; ++i) //各对结点之间初始已知路径及距离 for (j = 0; j < G.vexnum; ++j) { D_F[i][j] = G.arcs[i][j]; if (D_F[i][j] < MaxInt && i != j) Path_F[i][j] = i; //如果i和j之间有弧,则将j的前驱置为i else Path_F[i][j] = -1; //如果i和j之间无弧,则将j的前驱置为-1 } for (k = 0; k < G.vexnum; ++k) for (i = 0; i < G.vexnum; ++i) for (j = 0; j < G.vexnum; ++j) if (D_F[i][k] + D_F[k][j] < D_F[i][j]) { //从i经k到j的一条路径更短 D_F[i][j] = D_F[i][k] + D_F[k][j]; //更新D[i][j] Path_F[i][j] = Path_F[k][j]; //更改j的前驱为k } } void DisplayPath_Floyed(AMGraph G, int begin, int temp) { if (Path_F[begin][temp] != -1) { DisplayPath_Floyed(G, begin, Path_F[begin][temp]); cout << G.vexs[Path_F[begin][temp]] << "-->"; } } void main() { AMGraph G; int i, j, num_start, num_destination; VerTexType start, destination; CreateUDN(G); cout << endl; cout << "有向网G创建完成: "<< endl; for (i = 0; i < G.vexnum; ++i) { for (j = 0; j < G.vexnum; ++j) { if (j != G.vexnum - 1) { if (G.arcs[i][j] != MaxInt) cout << G.arcs[i][j] << " "; else cout << "∞" << " "; } else { if (G.arcs[i][j] != MaxInt) cout << G.arcs[i][j] << endl; else cout << "∞" << endl; } } } cout << " 迪杰特斯拉算法:"<<endl; cout << " 请依次输入起始点、终点名称:"; cin >> start >> destination; num_start = LocateVex(G, start); num_destination = LocateVex(G, destination); ShortestPath_DIJ(G, num_start); cout << endl << "最短路径为:"; DisplayPath_DIJ(G, num_start, num_destination); cout << G.vexs[num_destination] << endl; cout << "最短路径的长度为:" << D[num_destination] << endl; /****************************************/ cout << " 佛洛伊德算法:" << endl; ShortestPath_Floyed(G); cout << " 请依次输入路径的起点与终点的名称:"; cin >> start >> destination; num_start = LocateVex(G, start); num_destination = LocateVex(G, destination); cout << endl << "最短路径为:"; DisplayPath_Floyed(G, num_start, num_destination); cout << G.vexs[num_destination] << endl; cout << "最短路径的长度为:" << D_F[num_start][num_destination] << endl; cout << endl; }
运行结果: