前言
首先此篇文章是为低年级的朋友准备的,不涉及什么深奥的知识,比如线性规划之类的。仔细看,不要以为自己学不会,看不懂,只要你会DP并打过一些题目而且会单调队列优化DP,斜率DP离你就不远了~~~。这篇文章也是在我领悟了斜率DP不久写的,如果本文有什么不严谨的地方,欢迎指出!!!在此推荐一个大佬的BLOG,https://www.cnblogs.com/Xing-Ling/p/11210179.html,讲得很详细,如果你理解能力稍微强一点,可以看这篇文章,本文取自这篇博客的精华外加自己感受,换了一个简单点的题目方便理解。
斜率DP介绍
“斜率DP”,顾名思义就是通过斜率来优化DP,斜率式子(frac{y_1-y_2}{x_1-x_2})表示(x_1,y_1)和(x_2,y_2)两点的斜率。可以用斜率优化的式子通常可以写成(f[i]=min/max(f[j]+P(i)*Q(j))+H(i)),(P)和(H)是只与(i)有关的函数,(Q)是只与(j)有关的函数,单调队列优化解决不了的就在于既包含(i)又包含(j)的这一项(P(i)*Q(j)),于是诞生了斜率DP这么个东西,当然它对这个式子也有一个特殊要求,(P)和(Q)中至少有一个是单调递增/递减的(如果没有,据说可以用一些高级算法维护)。
- 如果有一个是单调的,可以优化到(O(n log_2 n));
- 如果有两个是单调的,也就是说满足决策单调性(以上BLOG有讲),可以优化到(O(n))。
至于为什么,请听下面分析。
理解斜率DP
这里以NOIP2010 四校联考模拟一 city为例。题目大意:有(n)个点,从第(i)个点到第(j)个点((i<j))的费用为((j-i)*a[i]+b[j]),求从第(1)个点到第(n)个点的最小费用。这题描述很简单。
那么由题列出的状态转移方程为(f[i]=min(f[j]+j*a[i]+b[j])-i*a[i](i<j)),可能看到这你有点疑问吧,为了让这题可做,我们从(n)~(1)枚举(i),至于为什么,学会了你可以自己顺着试试。我们把只含(i)的项提了出来,因为在每次算(f[i])时是不变的。普通做法的时间复杂度显然是(O(n^2))的,显然是过不了的。
设(j,k(0<i<k<j leq n))为(i)的决策点(一定要注意这里的大小关系),也就是可以转移到(i)的两点,且决策点(j)优于(或“相等“)(k),也就是费用更少。可以列出下面式子:
结论:我们得知,如果出现了这种情况(-a[i] geq frac{g[j]-g[k]}{j-k}),(j)是优于(包括相等)(k)的,同理,如果是(-a[i] leq frac{g[j]-g[k]}{j-k}),则是(k)(包括相等)优于(j)。我们把(j,k)看成x坐标;(g[j],g[k])看做y坐标,则代表决策点(j)的点的坐标为((j,g[j])),(k)为((k,g[k]))。**划重点(引用上文的博客,有改动):此处移项需要遵循的原则是:参变分离。将只与(i)有关的视作未知量,用其他的量来表示出只与(i)有关的量。最后的公式尽量化成(frac{y_1-y_2}{x_1-x_2}),而不是(frac{y_1-y_2}{x_2-x_1}),对于这种情况我们可以两边(*-1),注意要变号 **!!!
维护凸包
那么我们使用这个式子,维护一个凸包(用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集中所有的点——百度百科)。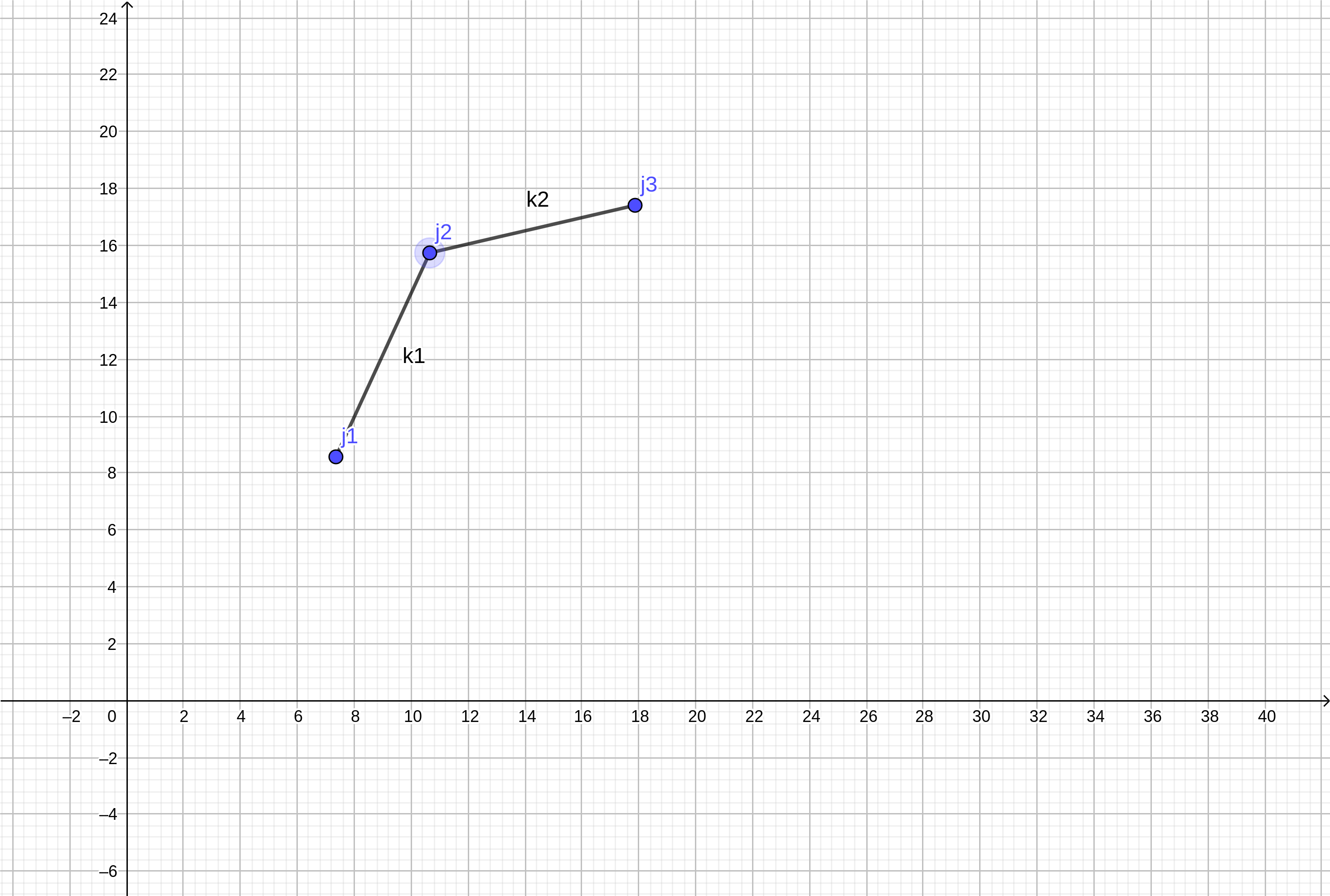
设有三个点(j1,j2,j3),他们都是已经求出了值的。(k1,k2)代表斜率。很明显可以看出(k2<k1),我们设(k0=-a[i])。有以下三种情况(为了应对以后不同大小的(k0),我们必须保证正确性,于是列出三种情况):
- (k2<k1 leq k0),由上述结论知,(j3优于j2优于j1);
- (k2 leq k0 <k1),由上述结论知,(j3和j1优于j2);
- (k0 leq k2 <k1),由上述结论知,(j1优于j2优于j3);
综上,无论哪种情况(j2)这个决策点都不是最优的,也就是在后续的DP中,不论(k0)多大,(j2)永远不会被用于更新一个点,它是没用的,我们把它删去。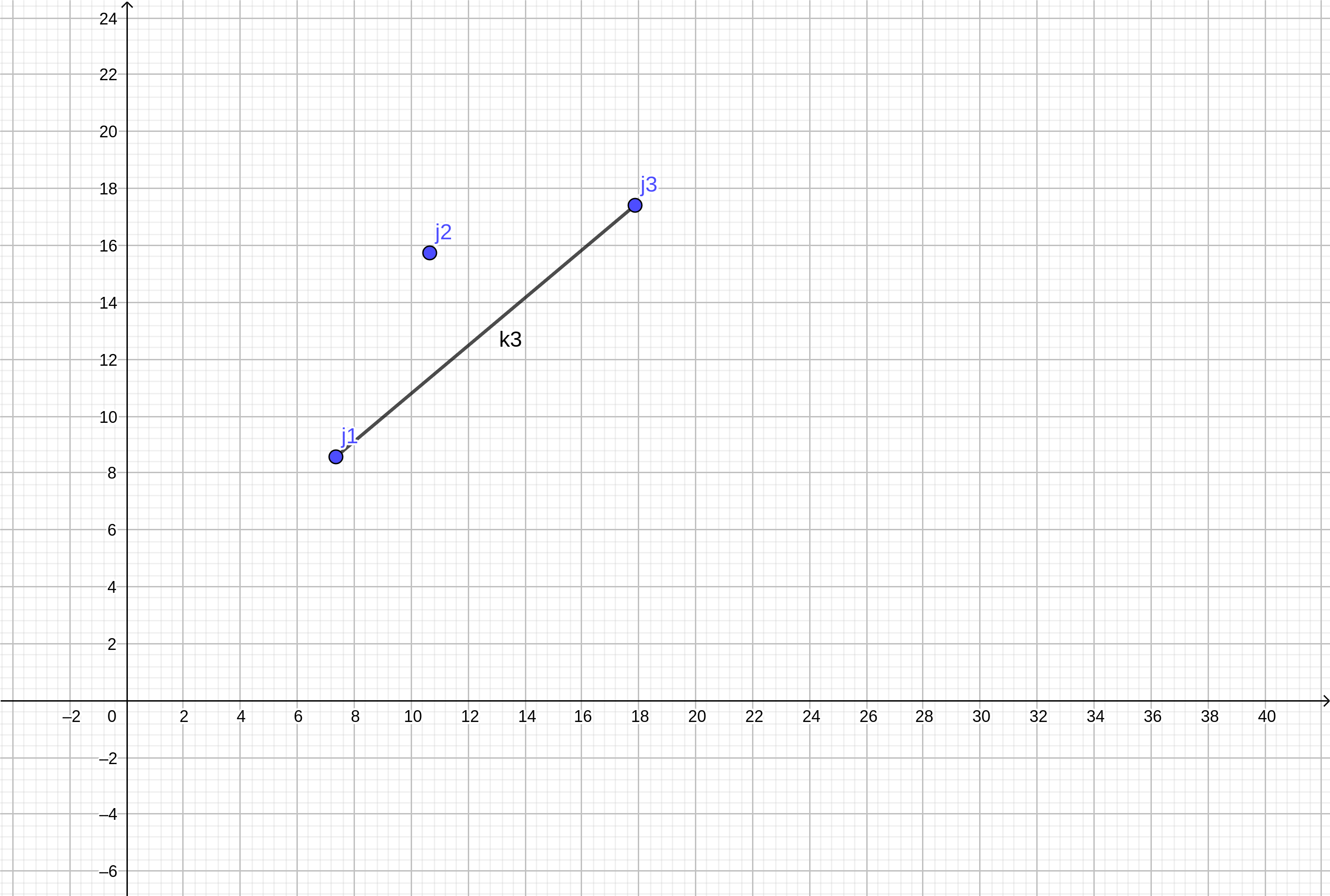
这个有什么用呢?维护凸包,说白了就是维护像单调队列优化那样的队列。这个队列中存在一个最优决策点,就是最优的那个,队列中的每个点都有可能为后续的DP做贡献。我们在(f[i])求完以后将它加入队列(如图的(j3)),并删除没用的点(如图的(j2))。在此贴上本题本部分代码
while(head<tail&&slope(q[tail-1],q[tail])<=slope(q[tail-1],i)) tail--;//slope函数是计算x,y两点的斜率;必须保证队列里至少有2个点
q[++tail]=i;//q是队列,存的是点的编号
二分答案
我们求(f[i])的时候,队列里必定存在着一个最优决策点,从它转移到(i)是最优的,通过以上的维护凸包,我们发现,对于这题我们维护的是下凸包(很形象,就是凸向下的),如果对于这题求花费最大,也就是把结论中的符号反过来维护的就是上凸包。不改变这题,相邻两个点间的斜率是递增的,如下图: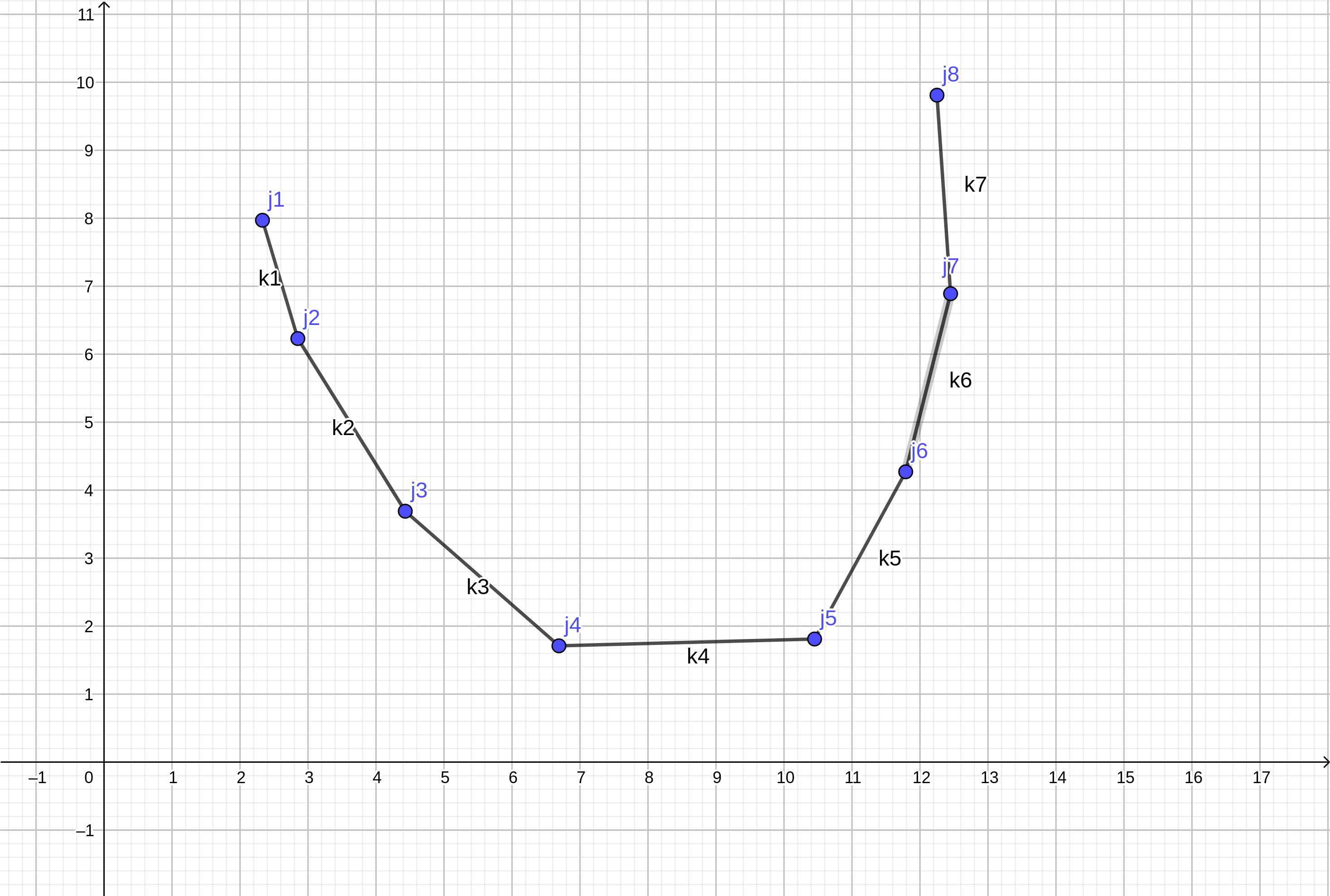
由于斜率是单调递增的,我们可以二分答案,那我们要二分找啥呢?
如上图:(k1<k2<k3<k4<k5<k6<k7),假设(k0)的大小是这样的:(k1<k2<k3 leq k0<k4<k5<k6)
我们发现,(k3 leq k0),由上述结论知,(j4优于j3);(k0<k4),由上述结论知,(j4优于j5)。其他以此类推。所以当前图中(j4)是最优决策点,我们二分一条线段的右端点,找到第一个斜率(>k0)的,它的上一个节点(也就是那条线段的左端点)即是最优决策点。如此,可以用(log_2 n)的时间求出最优决策点。需要注意的是二分这里有很多细节,我之前是二分左端点的,但是当所有的斜率都小于(k0)的时候,实际上最优的是最后一个点,但是我的程序二分到了倒数第二个端点,于是错了,卡了我好久,后开加了个特判过了。贴上代码(因为加了特判,写的很丑,见谅!同学们可以二分右端点):
l=head;
r=tail-1;
if(l==r){
if(slope(q[l],q[l+1])<-a[i]) l++;//只有两个点时无法二分
}else{
while(l<r){
mid=(l+r-1)/2;
if(slope(q[mid],q[mid+1])<-a[i]) r=mid;
else l=mid+1;
}
if(tail>head)
if(slope(q[l],q[l+1])>=-a[i]) l++;//特殊情况判断
}
//l即为最优决策点在队列中的下标
f[i]=f[q[l]]+(q[l]-i)*a[i]+b[q[l]];//用最优决策点更新f[i]
总结
实际上,斜率DP不是一个太难的东西,你可以把它想象成单调队列优化的工作模式,它的核心也是一个单调队列,但是它维护的规则与单调队列优化不一样,单调队列优化只是简单地基于数值维护,而斜率优化则是通过斜率维护,他们每加入一个新点时都要删去一些点。附上完整代码:
#include<cstdio>
int n,l,r,mid,head,tail,q[100005];
long long a[100005],b[100005],f[100005];
inline long double slope(int j,int k) {return (long double)((f[j]+b[j])-(f[k]+b[k]))/(long double)(j-k);}
int main(){
freopen("t3.in","r",stdin);
freopen("t3.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)
scanf("%lld",&b[i]);
f[n]=0;
head=tail=1;
q[1]=n;
for(int i=n-1;i>=1;i--){
l=head;
r=tail-1;
if(l==r){
if(slope(q[l],q[l+1])<-a[i]) l++;
}else{
while(l<r){
mid=(l+r-1)/2;
if(slope(q[mid],q[mid+1])<-a[i]) r=mid;
else l=mid+1;
}
if(tail>head)
if(slope(q[l],q[l+1])>=-a[i]) l++;
}
f[i]=f[q[l]]+(q[l]-i)*a[i]+b[q[l]];
while(head<tail&&slope(q[tail-1],q[tail])<=slope(q[tail-1],i)) tail--;
q[++tail]=i;
}
printf("%lld",f[1]);
return 0;
}