
要想实现高斯模糊的特点,则需要通过构建对应的权重矩阵来进行滤波。
1.3.1 正态分布

正态分布
正态分布中,越接近中心点,取值越大,越远离中心,取值越小。
计算平均值的时候,我们只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。正态分布显然是一种可取的权重分配模式。
1.3.2 高斯函数
如何反映出正态分布?则需要使用高函数来实现。
上面的正态分布是一维的,而对于图像都是二维的,所以我们需要二维的正态分布。

正态分布的密度函数叫做"高斯函数"(Gaussian function)。它的一维形式是:

其中,μ是x的均值,σ是x的方差。因为计算平均值的时候,中心点就是原点,所以μ等于0。

根据一维高斯函数,可以推导得到二维高斯函数:

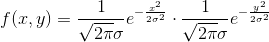
在运算的时候速度会加快很多,有了这个函数 ,就可以计算每个点的权重了。

更远的点以此类推。
为了计算权重矩阵,需要设定σ的值。假定σ=1.5,则模糊半径为1的权重矩阵如下:

这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵。

除以总值这个过程也叫做”归一问题“
目的是让滤镜的权重总值等于1。否则的话,使用总值大于1的滤镜会让图像偏亮,小于1的滤镜会让图像偏暗。

每个点乘以自己的权重值:

得到

将这9个值加起来,就是中心点的高斯模糊的值。
对所有点重复这个过程,就得到了高斯模糊后的图像。对于彩色图片来说,则需要对RGB三个通道分别做高斯模糊。

1.3.3 获取权重矩阵
假定中心点的坐标是(0,0),那么距离它最近的8个点的坐标如下:

更远的点以此类推。
为了计算权重矩阵,需要设定σ的值。假定σ=1.5,则模糊半径为1的权重矩阵如下:

这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵。

除以总值这个过程也叫做”归一问题“
目的是让滤镜的权重总值等于1。否则的话,使用总值大于1的滤镜会让图像偏亮,小于1的滤镜会让图像偏暗。
1.3.4 计算模糊值
有了权重矩阵,就可以计算高斯模糊的值了。
假设现有9个像素点,灰度值(0-255)如下:

每个点乘以自己的权重值:

得到

将这9个值加起来,就是中心点的高斯模糊的值。
对所有点重复这个过程,就得到了高斯模糊后的图像。对于彩色图片来说,则需要对RGB三个通道分别做高斯模糊。
1.3.5 边界值问题
既然是根据权重矩阵来进行处理的

如果一个点处于边界,周边没有足够的点,怎么办?
- ① 对称处理,就是把已有的点拷贝到另一面的对应位置,模拟出完整的矩阵。
- ② 赋0,想象图像是无限长的图像的一部分,除了我们给定值的部分,其他部分的像素值都是0
- ③ 赋边界值,想象图像是无限制长,但是默认赋值的不是0而是对应边界点的值
分别对x,y做一阶高斯滤波效果速度比较快
<!DOCTYPE html>
<html>
<head lang="en">
<meta charset="UTF-8">
<title>test</title>
</head>
<body>
<img src="./test.jpg" alt="img source" id="imgSource">
<canvas id="canvas"></canvas>
<script>
window.onload = function() {
var img = document.getElementById("imgSource"),
canvas = document.getElementById('canvas'),
width = img.width,
height = img.height;
// console.log(width);
canvas.width = width;
canvas.height = height;
var context = canvas.getContext("2d");
context.drawImage(img, 0, 0);
var canvasData = context.getImageData(0, 0, canvas.width, canvas.height);
//console.log(canvasData);
// 开始
var startTime = +new Date();
var tempData = gaussBlur1(canvasData, 8);
// var tempData = gosike(canvasData);
context.putImageData(tempData, 0, 0);
var endTime = +new Date();
console.log(" 一共经历时间:" + (endTime - startTime) + "ms");
}
/**
* 此函数为二重循环
*/
function gaussBlur(imgData, radius, sigma) {
var pixes = imgData.data,
width = imgData.width,
height = imgData.height;
radius = radius || 5;
sigma = sigma || radius / 3;
var gaussEdge = radius * 2 + 1; // 高斯矩阵的边长
var gaussMatrix = [],
gaussSum = 0,
a = 1 / (2 * sigma * sigma * Math.PI),
b = -a * Math.PI;
for (var i = -radius; i <= radius; i++) {
for (var j = -radius; j <= radius; j++) {
var gxy = a * Math.exp((i * i + j * j) * b);
gaussMatrix.push(gxy);
gaussSum += gxy; // 得到高斯矩阵的和,用来归一化
}
}
var gaussNum = (radius + 1) * (radius + 1);
for (var i = 0; i < gaussNum; i++) {
gaussMatrix[i] = gaussMatrix[i] / gaussSum; // 除gaussSum是归一化
}
//console.log(gaussMatrix);
// 循环计算整个图像每个像素高斯处理之后的值
for (var x = 0; x < width; x++) {
for (var y = 0; y < height; y++) {
var r = 0,
g = 0,
b = 0;
//console.log(1);
// 计算每个点的高斯处理之后的值
for (var i = -radius; i <= radius; i++) {
// 处理边缘
var m = handleEdge(i, x, width);
for (var j = -radius; j <= radius; j++) {
// 处理边缘
var mm = handleEdge(j, y, height);
var currentPixId = (mm * width + m) * 4;
var jj = j + radius;
var ii = i + radius;
r += pixes[currentPixId] * gaussMatrix[jj * gaussEdge + ii];
g += pixes[currentPixId + 1] * gaussMatrix[jj * gaussEdge + ii];
b += pixes[currentPixId + 2] * gaussMatrix[jj * gaussEdge + ii];
}
}
var pixId = (y * width + x) * 4;
pixes[pixId] = ~~r;
pixes[pixId + 1] = ~~g;
pixes[pixId + 2] = ~~b;
}
}
imgData.data = pixes;
return imgData;
}
function handleEdge(i, x, w) {
var m = x + i;
if (m < 0) {
m = -m;
} else if (m >= w) {
m = w + i - x;
}
return m;
}
/**
* 此函数为分别循环
*/
function gaussBlur1(imgData, radius, sigma) {
var pixes = imgData.data;
var width = imgData.width;
var height = imgData.height;
var gaussMatrix = [],
gaussSum = 0,
x, y,
r, g, b, a,
i, j, k, len;
radius = Math.floor(radius) || 3;
sigma = sigma || radius / 3;
a = 1 / (Math.sqrt(2 * Math.PI) * sigma);
b = -1 / (2 * sigma * sigma);
//生成高斯矩阵
for (i = 0, x = -radius; x <= radius; x++, i++) {
g = a * Math.exp(b * x * x);
gaussMatrix[i] = g;
gaussSum += g;
}
//归一化, 保证高斯矩阵的值在[0,1]之间
for (i = 0, len = gaussMatrix.length; i < len; i++) {
gaussMatrix[i] /= gaussSum;
}
//x 方向一维高斯运算
for (y = 0; y < height; y++) {
for (x = 0; x < width; x++) {
r = g = b = a = 0;
gaussSum = 0;
for (j = -radius; j <= radius; j++) {
k = x + j;
if (k >= 0 && k < width) { //确保 k 没超出 x 的范围
//r,g,b,a 四个一组
i = (y * width + k) * 4;
r += pixes[i] * gaussMatrix[j + radius];
g += pixes[i + 1] * gaussMatrix[j + radius];
b += pixes[i + 2] * gaussMatrix[j + radius];
// a += pixes[i + 3] * gaussMatrix[j];
gaussSum += gaussMatrix[j + radius];
}
}
i = (y * width + x) * 4;
// 除以 gaussSum 是为了消除处于边缘的像素, 高斯运算不足的问题
// console.log(gaussSum)
pixes[i] = r / gaussSum;
pixes[i + 1] = g / gaussSum;
pixes[i + 2] = b / gaussSum;
// pixes[i + 3] = a ;
}
}
//y 方向一维高斯运算
for (x = 0; x < width; x++) {
for (y = 0; y < height; y++) {
r = g = b = a = 0;
gaussSum = 0;
for (j = -radius; j <= radius; j++) {
k = y + j;
if (k >= 0 && k < height) { //确保 k 没超出 y 的范围
i = (k * width + x) * 4;
r += pixes[i] * gaussMatrix[j + radius];
g += pixes[i + 1] * gaussMatrix[j + radius];
b += pixes[i + 2] * gaussMatrix[j + radius];
// a += pixes[i + 3] * gaussMatrix[j];
gaussSum += gaussMatrix[j + radius];
}
}
i = (y * width + x) * 4;
pixes[i] = r / gaussSum;
pixes[i + 1] = g / gaussSum;
pixes[i + 2] = b / gaussSum;
// pixes[i] = r ;
// pixes[i + 1] = g ;
// pixes[i + 2] = b ;
// pixes[i + 3] = a ;
}
}
//end
imgData.data = pixes;
return imgData;
}
</script>
</body>
</html>