这份随笔是本人对B站斯坦福大学公开课:傅里叶变换及其应用 的学习笔记。
原课程网站:https://see.stanford.edu/Course/EE261
信号的周期化
我们希望建立的数学模型具有相当的普遍性,但并非所有的现象都是周期性的,实际的信号,最终都会结束,而 sin 和 cos 是无始无终的,永远持续下去。比如下图,信号只有在一段时间内的值非零,其余时间都是零。
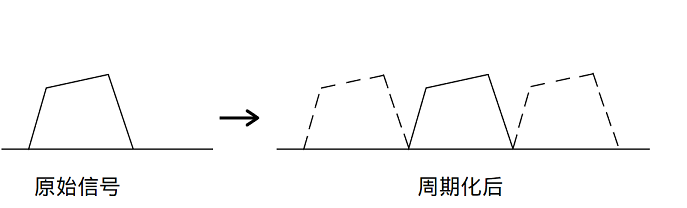
解决方法是,我们可以通过重复这个图形,把信号延申,使其具有时间上的周期性,即使我们只对其中一部分感兴趣,但对于数学分析,如果信号具有周期性,那他的性质对所有部分都适应。一般我们把这种方法叫做 信号的周期化。
我们可以利用这种思想来研究非周期信号。
假定周期
为了方便讨论,我们给周期现象假定周期为1,即
[f ( t + 1 ) = f ( t )
]
对于我们的数学模型,也使其周期为1,可以得到 sin(2πt) 与 cos(2πt)。
结论
我们可以使用 sin(2πt) 与 cos(2πt) 的组合来表示一般的周期为1的信号。
一个周期函数,包含多个频率成分
sin(2πt) 的最小正周期为 1,频率为 1,在1s内重复 1 次
sin(4πt) 的最小正周期为 1/2,频率为 2,在1s内重复 2 次
sin(6πt) 的最小正周期为 1/3,频率为 3,在1s内重复 3 次
但 1 都是他们的周期(比如sin(6πt) 把 3 次重复图形看成 1 次重复的图形)
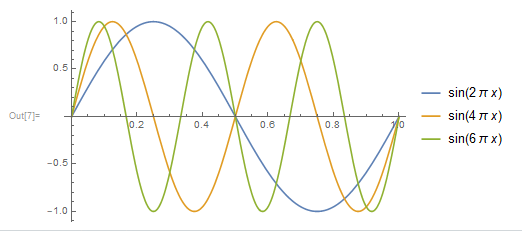
把他们加起来会怎么样?也就是 f(t)= sin(2πt) + sin(4πt) +sin(6πt) ,我们会得到
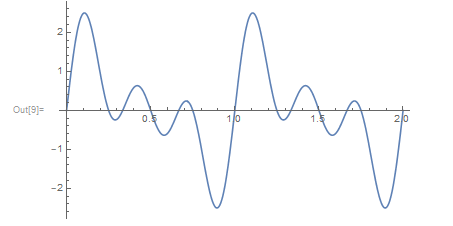
和式的周期是 1 .因为只有在最长周期的频率成分重复时,整个和式信号才重复一次。
这就是为什么一个周期,包含多个频率成分。而且,我们不单单可以改变频率,也可以改变振幅和相位。
结论:一个复杂的周期为1的信号,可以通过先变换正弦函数或余弦函数的频率,振幅,相位,然后相加获得。
即
[f(t)=sum _{k=1}^n A_k sin left(2 pi k t+varphi _k
ight)
]
其中,k是正整数,k=1的频率成分叫做基波,k>1的频率成分叫做谐波。
正余弦形式
运用和角公式化成正余弦形式
[sin left(varphi _k+2 ext{k$pi $t}
ight)=cos (2 ext{k$pi $t}) sin (varphi _k)+sin (2 pi k t) cos(varphi _k)
]
其中,(sin(varphi _k)) 和 (cos(varphi _k)) 是常数,所以可以得到我们常见的三角函数和式的形式:
[f(t)=sum _{k=1}^n left(a_kcos (2 pi k t)+b_ksin (2 pi k t)
ight)
]
(a_k) 和 (b_k) 和 振幅 A 有关。
这两种形式是等价的。
加上常数项(frac{a_0}{2})来表示其中不变的部分(为什么是(frac{a_0}{2})?,这只是另一种表达形式而已,方便计算):
[f(t)=frac{a_0}{2}+sum _{k=1}^n left( a_kcos (2 pi k t)+b_ksin (2 pi k t)
ight)
]
(frac{a_0}{2})在电子电力应用中,被称为直流成分。
指数形式
为了方便计算,我们在运算中,经常用的其实是指数形式。
根据欧拉公式,
[e^{2 pi i k t}=cos (2 pi k t) +i sin(2 pi ext{kt})
]
其中,i=(sqrt{-1})
得
[cos (2 pi k t)=frac{1}{2} left(e^{2 pi i k t}+e^{-2 pi i k t}
ight)
]
[sin (2 pi k t)=frac{1}{2i} left(e^{2 pi i k t}-e^{-2 pi i k t}
ight)
]
带入前面的三角函数形式的和式,
[�egin{align}
& a_k cos (2 pi k t)+ b_k sin (2 pi k t)\
=&frac{a_{k}(e^{-2 pi i k t}+e^{2 pi i k t})}{2}+frac{b_{k}(e^{2 pi i k t}-e^{-2 pi i k t})}{2}\
=&frac{1}{2} left(a_k e^{-2 pi i k t}+a_k e^{2 pi i k t}
ight)+frac{1}{2} left(b_k e^{2 pi i k t}-b_k e^{-2 pi i k t}
ight)\
=&frac{1}{2} left(a_k e^{-2 pi i k t}-b_k e^{-2 pi i k t}
ight)+frac{1}{2} left(a_k e^{2 pi i k t}+b_k e^{2 pi i k t}
ight)\
=&frac{1}{2} left(a_k-b_k
ight) e^{-2 pi i k t}+frac{1}{2} left(a_k+b_k
ight) e^{2 pi i k t}\
end{align}
]
从前面到这里,k还是正整数,它作为改变频率的系数,为了进一步化简,我们把复指数上正负号移到k上,与k结合,那么k就变成任意正负整数。复指数上正负号给予了“k”正负,但无论是正还是负,(a_k)和(b_k)的下标都对应正的。
[�egin{align}
&frac{1}{2} left(a_k-b_k
ight) e^{-2 pi i k t}+frac{1}{2} left(a_k+b_k
ight) e^{2 pi i k t}\
=&frac{1}{2} left(a_{- (-k)}-b_{- (-k)}
ight) e^{2 pi i (- k) t}+frac{1}{2} left(a_{+ (+k)}+b_{+ (+k)}
ight) e^{2 pi i (+ k) t}
end{align}
]
上式中,我们要把(-k)和(+k)看成一个整体,即此时,“k”还在实数域(其实这样描述不太准确,但为了区分两个域,我想不出更好描述,所以这里加了引号),(-k)代表k<0,(+k)代表k>0.。
所以这里的步骤,其实已经把三角函数形式的和式,进行分段操作,“k”进入复数域,是涵盖正负的整数,这样表示比较准确:
[frac{1}{2} left(a_k-b_k
ight) e^{-2 pi i k t}+frac{1}{2} left(a_k+b_k
ight) e^{2 pi i k t} o
�egin{array}{cc}
{ &
�egin{array}{cc}
frac{1}{2} left(a_{k}+b_{k}
ight) e^{2 pi i k t} & k>0 \
frac{1}{2} left(a_{-k}-b_{-k}
ight) e^{2 pi i k t} & k<0 \
end{array}
\
end{array}
]
我们把(frac{1}{2}(a_k+b_k))和(frac{1}{2}(a_k-b_k))统一用(C_k)表示
[C_k=
�egin{array}{cc}
{ &
�egin{array}{cc}
frac{1}{2}left(a_{+ k}+b_{+ k}
ight) & k>0 \
frac{1}{2}left(a_{- k}-b_{- k}
ight) & k<0 \
end{array}
\
end{array}
]
注意,(C_k)是分段函数.
将(C_k)代入分段函数化简,然后把各项频率分量相加,我们可以得到
[�egin{align}
&�egin{array}{cc}
{
�egin{array}{cc}
frac{1}{2} left(a_{k}+b_{k}
ight) e^{2 pi i k t} & k>0 \
frac{1}{2} left(a_{-k}-b_{-k}
ight) e^{2 pi i k t} & k<0 \
end{array}
\
end{array}
\
Longleftrightarrow & C_k e^{2 pi i k t}\
Longleftrightarrow &sum _{k=-n}^n C_k e^{2 pi i k t}\
end{align}
]
再思考一下,为什么k是从-n到n?
其实,这里的操作只是把原本的三角函数形式的和式,拆分为2次相加。
也就是说,在实数域中,三角函数形式的和式被分为两部分,在复数域我们需要两个式子相加,才能得到原本的实数域三角函数形式的和式。
比如在实域,当“k”=1时,
将三角函数形式的和式化为 tag(7)的形式为
[frac{1}{2} left(a_{ 1}-b_{ 1}
ight) e^{2 pi i (- 1) t}+frac{1}{2} left(a_{ 1}+b_{ 1}
ight) e^{2 pi i ( 1) t}\
]
在复数域,当“k”=1时
(C_k=frac{1}{2}(a_k+b_k)),
我们进行回推,得到
[�egin{align}
& C_1 e^{2 pi i 1 t}\
=&frac{1}{2} left(a_{1}+b_{1}
ight) e^{2 pi i (1) t}\
end{align}
]
我们需要加上“k”=-1,才能回推到实域
在复数域,当“k”=-1时,
(C_k=frac{1}{2}left(a_{- k}-b_{- k}
ight )),
我们进行回推 ,得到
[�egin{align}
& C_{-1} e^{2 pi i (-1) t}\
=&frac{1}{2} left(a_{1}-b_{1}
ight) e^{2 pi i (-1) t}\
end{align}
]
我们看到,要把两个指数形式的式子 相加,才能得到三角函数形式.
相加的和,还是实数,因为 两个指数形式 的式子满足共轭关系。
至此,我们就对普遍的周期性信号或现象完成了建模,我们得到最终简化的式子
[�egin{align}
f(t)=&sum _{k=-n}^n C_k e^{2 pi i k t}\
end{align}
]
其中,我们假定 f(t) 周期为1。
和式中的系数
假设我们建模问题已经解决,我们对某个周期性信号建模:
[�egin{align}
f(t)=&sum _{k=-n}^n C_k e^{2 pi i k t}\
end{align}
]
f(t)是我们已经得到的信号,那么式子中未知量就是(C_k)。怎么求出(C_k)?
先用代数运算,从和式中取出(C_m)项
[C_m e^{2 pi i m t}=f(t) -sum _{k
eq m} C_k e^{2 pi i k t}
]
[C_m=f (t) e^{-2 pi i m t}-sum _{k
eq m} C_k e^{2 pi i t (k-m)}
]
两边同时积分,
[int_0^1 C_m \, dt=C_m\
C_m=int_0^1 f (t) e^{-2 pi i m t} \, dt-sum _{k
eq m} C_k int_0^1 e^{2 pi i (k-m)t} \, dt
]
[�egin{align}
&int_0^1 e^{2 pi i (k-m)t} \, dt\
=&frac{e^{2 pi i (k-m)}-e^0}{2 pi i (k-m)}\
&欧拉公式变换\
=&frac{i sin (2 pi (k-m))+cos (2 pi (k-m))-1}{2 pi i (k-m)}\
=&frac{0+1-1}{2 pi i (k-m)}\
=&0
end{align}
]
(K-M)是整数,所有累加项的和消失,剩下
[C_m=int_0^1 f (t) e^{-2 pi i m t} \, dt
]
给定 f(t) ,我们就能求出对应分量的系数。


