时变磁场的计算
导线连接圆形电容,电容半径为 (R) ,通电的时候,会在电容内部产生一个变化的电场E。
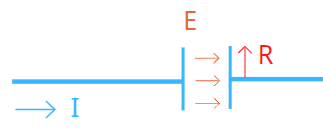
静态时,我们可以计算电容内部电场为
但由于给电容通电,(Q_{free}) 在不断增加,电场变化的,为 (frac{ ext{dE}}{ ext{dt}}) ,根据电流定义:
可得变化的电场为
只有电流为0时,电容内部才没有变化的电场。
通电瞬间,中间有电介质电容,电荷在极板上不断聚集,同时电介质不断的极化,感应电荷不断重新排列(电荷移动——内部有电流),当极板上的正负电荷达到一定程度,与电源提供的电场大小相同时,电荷不再聚集,电介质不再极化时,此时电流就为0。但是在真空电介质中,电容内部是没有电流的。
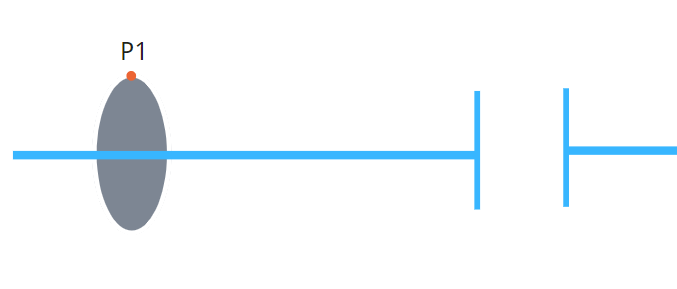
在距离导线 (r) 处取一点 (P_1) ,在电容上方距离导线相同距离的地方取一点 (P_2)。

我们关心的是,(P_1) 和 (P_2) 点的磁场是多少?由于电容是开口的,没有电流流过,怎么计算?
计算磁场大小,我们前面学过了毕奥萨法尔定律和安培定律,理论上毕奥萨法尔定律可以计算,但是电流会流到电容圆形极板上,显然很难计算。故用安培定律计算。
计算 (P_1) 处磁感应强度
选择半径为 (r) 的闭合圆环应用安培定律,给圆环加上一个开曲面,先可以直接选择这个平面。
应用安培定律可得
故
依然选择半径为 (r) 的闭合圆环应用安培定律,但给圆环加上一个穿过电容内部的开曲面,因为电容内部是开路的,没有电流穿过开曲面。

应用安培定律
现在计算结果为0。
计算 (P_2) 处磁感应强度
同 (P_1) 一样,选择半径为 (r) 的闭合圆环,给圆环加上一个开曲面,先可以直接选择这个平面。

应用安培定律
故
显然出错了,计算有问题。
这说明,安培环路定律不够完善。前面的安培环路定律只能研究恒定磁场与直流(传导电流)之间的关系。
修正的安培环路定理与位移电流
麦克斯韦大佬作出了解释。他认为不论闭合曲线包围的开曲面形状如何,都应该得到相同的结果。
麦克斯韦对安培定律进行了完善。
他推理,法拉第定律指出,变化的磁通量会激发电场,那么也许变化的电通量会激发磁场。
开曲面中电通量为
电容有“电流""时,必须有变化的电场。麦克斯韦提出,我们必须加上电通量的导数。
修正的安培环路定理:
其中
麦克斯韦将这一项记为 "位移电流" 。
实际上后面还需要修正。
但现在我们得到计算磁场的工具。
重新考虑 (P_1)
计算(P_1) 处磁感应强度
如果直接选择圆环内平面作为开曲面,没有电场穿过开曲面,显然位移电流项为0,故
如果选择一个穿过电容内部的开曲面,没有电流穿过开曲面,第一项电流为0,第二项加入电通量的导数,假设电容没有边缘场,则电通量就是 $ E pi R^2$ ,
可得
结果相同。
一种是位移电流项没有贡献,一种是传导电流项没有贡献。
电容内部的磁场
现在我们可以计算电容内部任何地方的磁场。
假设 (P_2) 在距离导线 (r<R) 的距离,直接选择圆环内平面作为开曲面,有电场穿过。
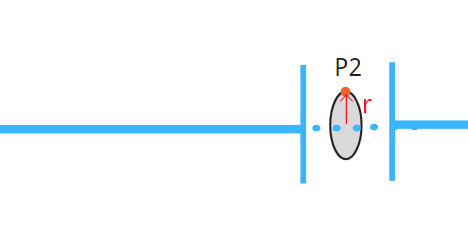
应该修正后的安培环路定理,注意开曲面表面积是 (pi r^2)
可得
我们可以画出电容磁感应强度关于距离 (r) 曲线图
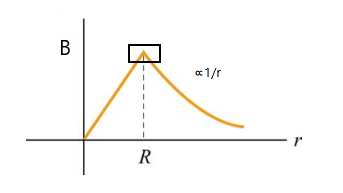
但实际上,接近边缘时是不正常的(方框,也就是 $r=R $),因为我们假设了边缘场为0,不同电容有不同的边缘场,很难准确计算,所以很难改正。