最近参照一些资料实现了一个非常简易的正则表达式引擎,支持基本的正则语法 | + * ()等。
实现思路是最基本的:正则式->AST->NFA->DFA。
以下是具体步骤:
一. 正则式->AST:
这一步没什么好说的,因为正则表达式的语法较为简单,使用编译原理中的递归下降的方法, 可以很容易的构造出一个语法分析器。
二. AST->NFA:
这里的NFA准确的来说应该是ε-NFA,即带有ε边的非确定的有穷状态自动机。ε边是指可以在不接受任何字符的情况下转移的边。其存在的意义是状态与状态之间的组合。从而更方便的将AST转化成ε-NFA。
正则的基本元素及状态的构造方法:
1.字符集
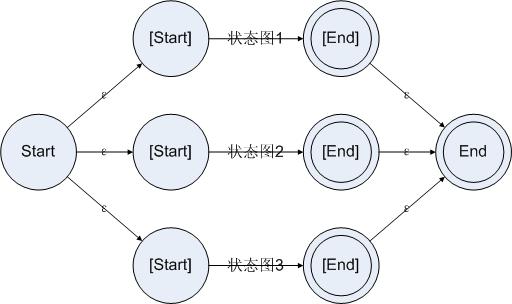
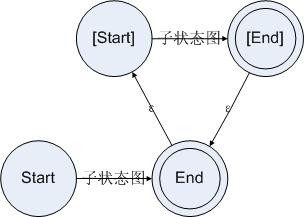
2.串联
从这里开始,我们便要使用ε边,以便将不同状态连接起来。
3.并联
4.重复(>0次)
5.可选(>=0次)
将重复的start删除,再让原end同时具备start和end即可。
在此处,我犯了一个错误。对于重复,我直接将要重复的子状态的end与start间建立了一条ε边,实现了同样的功能。我想将同样的思路应用于可选,便在重复的基础上在start与end间建立ε边,而这导致了状态通过ε边形成环路,从而使得下一步骤中ε闭包的寻找陷入死循环。
三. 消除ε边及无效状态
- 找到有效状态
有效状态的是开始状态加上所有存在非ε边的输入的状态。结束状态不一定是有效状态,但是如果存在一个有效状态可以仅通过ε边到达结束状态的话,那么这个状态应该被标记为结束状态。 - 添加必要的边
对所有有效状态,寻找其ε闭包。ε闭包是指从该状态仅通过ε边所能到达的状态集合(不包含该状态),此处使用BFS即可。并将闭包看做整体,将从闭包延伸出的边复制到该有效状态上。 - 删除所有ε边和无效状态
四. NFA->DFA
此处使用子集构造算法,主要思路就是将一个状态经过相同的转移条件所能到达的状态合并,看做一个DFA状态,再对这个DFA状态采取相同做法,重复执行。最后得到DFA状态表。
五. DFA->状态转移表
这一步就是将上一步得到的DFA表转换成一个字符表,记录每个状态接收某个字符能够转移到的状态。
最后,该引擎我还未完成,目前还不支持贪婪、非贪婪,捕获,边界,以及各种“黑魔法”(这么看来好像有点太简陋了)。只能说自己的编码水平还远远不够吧_(:з」∠)_。
代码:https://github.com/CknightX/Regex (好多bug未修复。。)
(本文的内容和图片主要参考自vczh《构造可配置词法分析器》和《正则表达式》)