
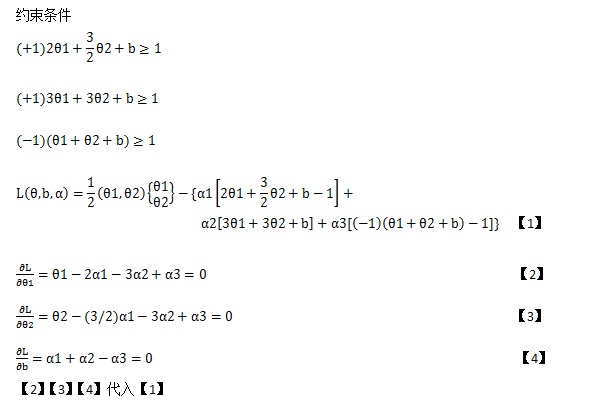


说明:
1)α2=0表示第二个样例不在分类面上,在分类面上的点αi均不为零。
2)二次项矩阵,可以通过矩阵相乘相加方法得到,如上例
3)目标函数变为负值,是为了照顾matlab的标准型。
假定应用多项式核(核方法) 样本使用此前的样本。

若有新元素(0,0)需要分类。
则Y(0,0) = ,则(0,0)为负例
利用核方法后,支持向量代入后不再为+1,或者-1.即Y(1,1)!=-1,Y(2,3/2)!=1。这个我还没搞明白为什么,希望有朋友能告诉我。
将x1,x2通过核函数转化为 x1*x1,x1*x2,x2*x1,x2*x2,原语料转化为
4,3,3,9/4 +
9,9,9,9 +
1,1,1,1 -
按照类似的解法解得:
Y=(< (4,3,3,9/4),(x1,x2,x3,x4) > - < (1,1,1,1),(x1,x2,x3,x4) > + b
解得b=-17.53125
Y=[(< (4,3,3,9/4),(x1,x2,x3,x4) > - < (1,1,1,1),(x1,x2,x3,x4) >+ -17.53125
除以9.28125得到:
Y=(< (0.4310 0.3232 0.3232 0.2424),(x1,x2,x3,x4) > - < (0.1077 0.1077 0.1077 0.1077),(x1,x2,x3,x4) > + -1,8889
这样:
Y(2,3/2) = +1
Y(1,1) = -1
因此没有比较纠结支持向量是否为+1或者-1,只需要正例为+r,负例为-r即可,最小的r,最大的-r均有支持向量获得。