参考:
《啊哈!算法》p.155
https://www.cnblogs.com/dailinfu/p/7398112.html
该算法用于解决一个点到其余各顶点的最短路径

先来一张图,求1点到6点的最短路径
先用一个二维数组用于存储这张图

还有一个一维数组存储1点到各点的距离

我们将此时dis数组中的值称为最短路程的“估计值”。
既然是求1号顶点到其余各个顶点的最短路程,那就先找一个离1号顶点最近的顶点。通过数组dis可知当前离1号顶点最近的是2号顶点。当选择了2号顶点后,dis[2]的值就已经从“估计值”变为了“确定值”,即1号顶点到2号顶点的最短路程就是当前dis[2]值。为什么呢?你想啊,目前离1号顶点最近的是2号顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得1号顶点到2号顶点的路程进一步缩短了。 因为1号顶点到其他顶点的路程肯定没有1号到2号顶点短,对吧O(∩_∩)O~
既然选了2号顶点,接下来再来看2号顶点有哪些出边呢。有2→3和2→4这两条边。先讨论通过2→3这条边能否让1号顶点到3号顶点的路程变短,也就是说现在来比较dis[3]和dis[2]+e[2][3]的大小。其中dis[3]表示1号顶点到3号顶点的路程; dis[2]+e[2][3]中 dis[2]表示1号顶点到2号顶点的路程,e[2][3]表示2→3这条边。所以
dis[2]+e[2][3]就表示从1号顶点先到2号顶点,再通过2→3这条边,到达3号顶点的路程。
我们发现dis[3]=12, dis[2]+e[2][3]=1+9=10, dis[3]>dis[2]+e[2][3], 因此dis[3]要更新为10。这个过程有个专业术语叫做“松弛”,1 号顶点到3号顶点的路程即dis[3],通过2→3这条边松弛成功。这便是Dijkstra算法的主要思想:通过“边”来松弛1号顶点到其余各个顶点的路程。
同理,通过2→4 (e[2][4]), 可以将dis[4]的值从∞松弛为4 (dis[4]初始为∞,dis[2]+e[2][4]=1+3=4, dis[4]>dis[2]+e[2][4], 因此dis[4]要更新为4)。
刚才我们对2号顶点所有的出边进行了松弛。松弛完毕之后dis数组为:
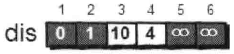
接下来,继续在剩下的3、4、5和6号顶点中,选出离1号顶点最近的顶点。通过上面更新过的dis数组,当前离1号顶点最近的是4号顶点。此时,dis[4]的值已经从“估计值”变为了“确定值”。 下面继续对4号顶点的所有出边(4-->3,4-->5和4-->6)用刚才的方法进行松弛。松弛完毕之后dis数组为:
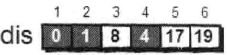

继续在剩下的5和6号顶点中,选出离1号顶点最近的顶点,这次选择5号顶点。此时,dis[5]的值已经从“估计值”变为了“确定值”。对5号顶点的所有出边(5-->4)进行松弛。松弛完毕之后dis 数组为:

最终dis数组如下,这便是1号顶点到其余各个顶点的最短路径。

OK,现在来总结一下刚才的算法。算法的基本思想是:每次找到离源点(. 上面例子的源点就是1号顶点)最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。基本步骤如下:
1.将所有的顶点分为两部分:已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始,已知最短路径的顶点集合P中只有源点一个顶点。我们这里用一个book数组来记录哪些点在集合P中。例如对于某个顶点i,如果book[i]为1则表示这个顶点在集合P中,如果book[i]为0则表示这个顶点在集合Q中。
2.设置源点s到自己的最短路径为0即dis[s]=0。若存在有源点能直接到达的顶点i,则把dis[i]设为e[s][i]。同时把所有其他(源点不能直接到达的)顶点的最短路径设为∞。
3. 在集合Q的所有顶点中选择一个离源点s最近的顶点u (即dis[u]最小) 加入到集合P。并考察所有以点u为起点的边,对每一条边进行松弛操作。例如存在一条从u到v的边,那么可以通过将边u→v添加到尾部来拓展一条从s到v的路径,这条路径的长度是dis[u]+e[u][v]。 如果这个值比目前已知的dis[v]的值要小,我们可以用新值来替代当前dis[v]中的值。
4. 重复第3步,如果集合Q为空,算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。
贴出完整算法
/*Dijkstra算法,即单源最短路径算法:通过边实现松弛*/
#include<stdio.h>
int main()
{
int i,j,n,m,u,v,t1,t2,t3,min;
int dis[10];
int e[10][10];
int book[10];
int inf=99999999;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j) e[i][j]=0;
else e[i][j]=inf;
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&t1,&t2,&t3);
e[t1][t2]=t3;
}
//初始化dis数组,1号到各个顶点的初始路程
for(i=1;i<=n;i++)
dis[i]=e[1][i];
for(i=1;i<=n;i++)
book[i]=0;
book[1]=1;
//Dijkstra核心算法
for(i=1;i<=n-1;i++)
{
//找到离1号顶点最近的顶点
min=inf;
for(j=1;j<=n;j++)
{
if(book[j]==0 && dis[j]<min)
{
min=dis[j];
u=j;
}
}
book[u]=1; //这一步漏了,一定要记住走过的顶点一定要标记
for(v=1;v<=n;v++)
{
if(e[u][v]<inf) //自己做的时候,还少了以这一步 是否应该改成if(book[v]==0 && e[u][v]<inf)
{
if(dis[v]>dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
for(i=1;i<=n;i++)
printf("%5d",dis[i]);
getchar();getchar();
return 0;
}
/*
input:
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
output:
0 1 8 4 13 17
* /
vector 邻接表版本
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
#include<cstdlib>
#define N 11000
#define INF 0x3f3f3f3f
using namespace std;
int n,m,a,b,c,vis[N],dis[N];
struct node
{
int d,w;
};//定义一个结构体来存储每个入度点以及对应边的权值
//比如边u->v,权值为w,node结构体存储的就是v以及w。
vector<node>v[N];
void dijkstra(int u);
int main()
{
//对于N非常大但是M很小的这种稀疏图来说,用邻接矩阵N*N是存不下的。邻接矩阵是将所有的点都存储下来了,然而
//对于稀疏图来说,有很多点是没有用到的,把这些点也存储下来的话就会很浪费空间。可以用邻接表来存储,这里借助vector来实现邻接表的操作。
//用邻接表存储时候,只存储有用的点,对于没有用的点不存储,实现空间的优化。
cin>>n>>m;
for(int i=0; i<=n; i++)
v[i].clear();//将vecort数组清空
for(int i=1; i<=m; i++) //用vector存储邻接表
{
node nd;
scanf("%d%d%d",&a,&b,&c);
nd.d=b,nd.w=c;//将入度的点和权值赋值给结构体
v[a].push_back(nd);//将每一个从a出发能直接到达的点都压到下标为a的vector数组中,以后遍历从a能到达的点就可以直接遍历v[a]
// nd.d=a,nd.w=c;//无向图的双向存边
// v[b].push_back(nd);
}
dijkstra(1);
if(dis[n]!=INF)
printf("%d
",dis[n]);
else
printf("-1");
return 0;
}
void dijkstra(int u)
{
//初始位置从顶点1开始。
memset(vis,0,sizeof(vis));//初始化标记数组
for(int i=0; i<=n; i++)
dis[i]=INF;//先将dis初始化为无穷大,下面更新dis的初始值。
dis[u]=0;
//初始化dis数组,1号到各个顶点的初始路程
for(int i=0;i<v[u].size();i++)
dis[v[u][i].d]=min(v[u][i].w,dis[v[u][i].d]);//可能存在重边和自环
for(int i=1;i<=n-1;i++)
{
//找到离1号顶点最近的顶点
int minn=INF;
int k=0;
for(int j=1;j<=n;j++)
if(vis[j]==0&&dis[j]<minn)//f[j]==0,未添加的点
minn=dis[j],k=j;
vis[k]=1;
if(k==0)break;
for(int p=0;p<v[k].size();p++)//v[k].size 个点与k相连
{
if(v[k][p].w+dis[k]<dis[v[k][p].d])//比较
dis[v[k][p].d]=v[k][p].w+dis[k];
}
}
}
但是这个算法的时间复杂度是0(N^2).我希望他的时间复杂度降为0((M+N)logN)
使用邻接矩阵实现的Djjkstra算法的复杂度是O(V^2)。使用邻接表的话,更新最短距离只需要访问每条边一次即可,因此这部分的复杂度是O(E)。但是每次要枚举所有的顶点来查找下一个使用的顶点,因此最终复杂度还是0(V)。在E比较小时,大部分的时间花在了查找下一个使用的顶点上,因此需要使用合适的数据结构对其进行优化。
需要优化的是数值的插入(更新)和取出最小值两个操作,因此使用堆就可以了。把每个顶点当前的最短距离用堆维护,在更新最短距离时,把对应的元素往根的方向移动以满足堆的性质。而每次从堆中取出的最小值就是下一次要使用的顶点。这样堆中元素共有O(V)个,更新和取出数值的操作有O(E)次,因此整个算法的复杂度是 O(ElogV)。
下面是使用STL的priority_ queue ”的实现。在每次更新时往堆里插人当前最短距离和顶点的值对。插人的次数是O(E)次,因此元素也是0(E)个。当取出的最小值不是最短距离的话,就丢弃这个值。这样整个算法也可以在同样的复杂度内完成。
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
#include<cstdlib>
#include<queue>
#define N 100005
#define INF 0x3f3f3f3f
using namespace std;
int n,m,a,b,c,dis[N];
typedef pair<int,int> P;
struct node
{
int d,w;
};//定义一个结构体来存储每个入度点以及对应边的权值
//比如边u->v,权值为w,node结构体存储的就是v以及w。
vector<node>G[N];
void dijkstra(int u);
int main()
{
//对于N非常大但是M很小的这种稀疏图来说,用邻接矩阵N*N是存不下的。邻接矩阵是将所有的点都存储下来了,然而
//对于稀疏图来说,有很多点是没有用到的,把这些点也存储下来的话就会很浪费空间。可以用邻接表来存储,这里借助vector来实现邻接表的操作。
//用邻接表存储时候,只存储有用的点,对于没有用的点不存储,实现空间的优化。
cin>>n>>m;
for(int i=0; i<=n; i++)
G[i].clear();//将vecort数组清空
for(int i=1; i<=m; i++) //用vector存储邻接表
{
node nd;
scanf("%d%d%d",&a,&b,&c);
nd.d=b,nd.w=c;//将入度的点和权值赋值给结构体
G[a].push_back(nd);//将每一个从a出发能直接到达的点都压到下标为a的vector数组中,以后遍历从a能到达的点就可以直接遍历v[a]
// nd.d=a,nd.w=c;//无向图的双向存边
// v[b].push_back(nd);
}
dijkstra(1);
if(dis[n]!=INF)
printf("%d
",dis[n]);
else
printf("-1");
return 0;
}
void dijkstra(int u)
{
priority_queue<P, vector<P>, greater<P> > que;
for(int i=0; i<=n; i++)
dis[i]=INF;//先将dis初始化为无穷大,下面更新dis的初始值。
dis[u]=0;
que.push(make_pair(0,u));
while (!que.empty()) {
P p=que.top();
que.pop();
int v=p.second;
if(dis[v]!=p.first) continue;
for (int i = 0; i < G[v].size(); ++i) {
node e=G[v].at(i);
if(dis[e.d]>dis[v]+e.w){
dis[e.d]=dis[v]+e.w;
que.push(make_pair(dis[e.d],e.d));
}
}
}
}
java版本解法:
package 最短路径;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
static class Edge{
int to;
int cost;
}
static class P implements Comparable<P>{
int dis;
int index;
public P(int dis, int index) {
this.dis = dis;
this.index = index;
}
@Override
public int compareTo(P o) {
return this.dis>o.dis?1:-1;
}
}
static int MAX_V=100000;
static int MAX_E=200000;
static int INF=10000;
static ArrayList<Edge> G[]=new ArrayList[MAX_V];
static int V;
static int E;
static int S;
static int d[]=new int[MAX_V];
public static void main(String[] args) {
for (int i = 0; i < MAX_V; i++) {
G[i]=new ArrayList<Edge>();
}
Scanner sc=new Scanner(System.in);
V=sc.nextInt();
E=sc.nextInt();
S=sc.nextInt();
S--;
for (int i=0; i<E; i++)
{
int s=sc.nextInt();
int t=sc.nextInt();
int c=sc.nextInt();
Edge e=new Edge();
e.to=t-1;e.cost=c;
G[s-1].add(e);
}
dijkstra(S);
for (int i=0; i<V; i++)
if (d[i]!=INF) System.out.printf("%d ", d[i]);
else System.out.printf("%d ", 2147483647);
}
static void dijkstra(int s)
{
Arrays.fill(d,INF);
d[s]=0;
PriorityQueue<P> que=new PriorityQueue<>();//默认小根堆
que.add(new P(0,s));
while (!que.isEmpty())
{
P p=que.poll();
int v=p.index;
if (d[v]<p.dis) continue;
for (int i=0; i<G[v].size(); i++)
{
Edge e=G[v].get(i);
if (d[e.to]>d[v]+e.cost)
{
d[e.to]=d[v]+e.cost;
que.add(new P(d[e.to], e.to));
}
}
}
}
}
4 5
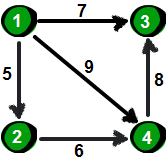
第一行两个整数n,m分别代表点的个数,路线的数量。
接下来的五行x,y,z.代表点x到点y的距离z。
存储的结构是这样的。就像hashmap

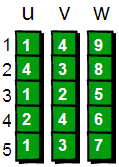
再用一个first数组来存储每个顶点其中一条边的编号。以便待会我们来枚举每个顶点所有的边(你可能会问:存储其中一条边的编号就可以了?不可能吧,每个顶点都需要存储其所有边的编号才行吧!甭着急,继续往下看)。比如1号顶点有一条边是 “1 4 9”(该条边的编号是1),那么就将first[1]的值设为1。如果某个顶点i没有以该顶点为起始点的边,则将first[i]的值设为-1。现在我们来看看具体如何操作,初始状态如下。
咦?上图中怎么多了一个next数组,有什么作用呢?不着急,待会再解释,现在先读入第一条边“1 4 9”。
读入第1条边(1 4 9),将这条边的信息存储到u[1]、v[1]和w[1]中。同时为这条边赋予一个编号,因为这条边是最先读入的,存储在u、v和w数组下标为1的单元格中,因此编号就是1。这条边的起始点是1号顶点,因此将first[1]的值设为1。
另外这条“编号为1的边”是以1号顶点(即u[1])为起始点的第一条边,所以要将next[1]的值设为-1。也就是说,如果当前这条“编号为i的边”,是我们发现的以u[i]为起始点的第一条边,就将next[i]的值设为-1(貌似的这个next数组很神秘啊⊙_⊙)。
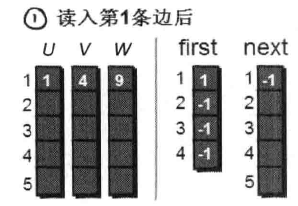
读入第2条边(4 3 8),将这条边的信息存储到u[2]、v[2]和w[2]中,这条边的编号为2。这条边的起始顶点是4号顶点,因此将first[4]的值设为2。另外这条“编号为2的边”是我们发现以4号顶点为起始点的第一条边,所以将next[2]的值设为-1。
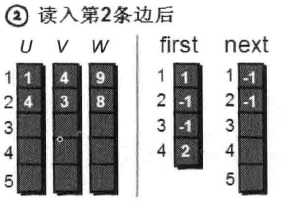
读入第3条边(1 2 5),将这条边的信息存储到u[3]、v[3]和w[3]中,这条边的编号为3,起始顶点是1号顶点。我们发现1号顶点已经有一条“编号为1 的边”了,如果此时将first[1]的值设为3,那“编号为1的边”岂不是就丢失了?我有办法,此时只需将next[3]的值设为1即可。现在你知道next数组是用来做什么的吧。next[i]存储的是“编号为i的边”的“前一条边”的编号。
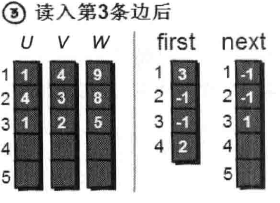
读入第4条边(2 4 6),将这条边的信息存储到u[4]、v[4]和w[4]中,这条边的编号为4,起始顶点是2号顶点,因此将first[2]的值设为4。另外这条“编号为4的边”是我们发现以2号顶点为起始点的第一条边,所以将next[4]的值设为-1。
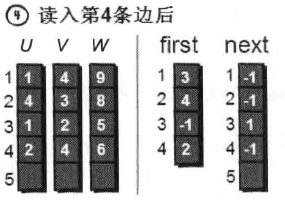
读入第5条边(1 3 7),将这条边的信息存储到u[5]、v[5]和w[5]中,这条边的编号为5,起始顶点又是1号顶点。此时需要将first[1]的值设为5,并将next[5]的值改为3。
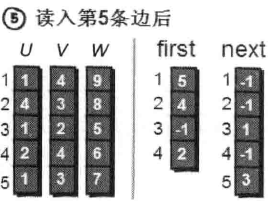
接下来如何遍历每一条边呢? 我们之前说过其实first 数组存储的就是每个顶点i (i从1~n) 的第一条边。比如1号顶点的第一条边是编号为5的边(1 3 7), 2号顶点的第一条边是编号为4的边(2 4 6), 3号顶点没有出向边, 4号顶点的第一条边是编号为2的边(2 4 6)。那么如何遍历1号顶点的每一条边呢?也很简单。请看下图:
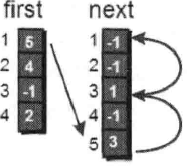
核心代码
int n,m,i;
//u、v和w的数组大小要根据实际情况来设置,要比m的最大值要大1
int u[6],v[6],w[6];
//first和next的数组大小要根据实际情况来设置,要比n的最大值要大1
int first[5],next[5];
scanf("%d %d",&n,&m);
//初始化first数组下标1~n的值为-1,表示1~n顶点暂时都没有边
for(i=1;i<=n;i++)
first[i]=-1;
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&u[i],&v[i],&w[i]);//读入每一条边
//下面两句是关键啦
next[i]=first[u[i]];
first[u[i]]=i;
}