求非线性规划
min f(x)= x(1)^2 + x(2)^2 + 8
s.t. { x(1)^2-x(2)>=0 ,
-x(1) - x(2)^2 +2 = 0,
x(1)>=0 ,x(2)>=0 }
首先定义增广目标函数 编写M函数 fitness.m

function g =fitness(x) M=5000000; f=x(1)^2+x(2)^2+8; g=f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);
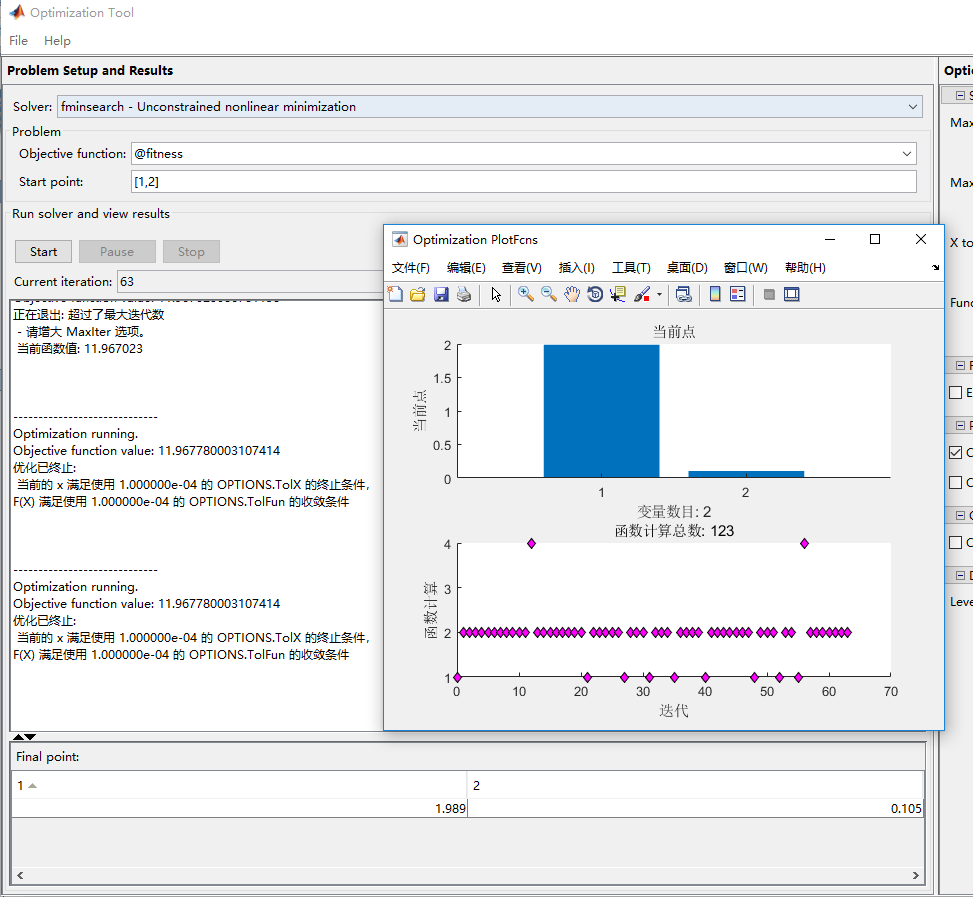
三次最小寻优 函数值接近最优解
