polyshape
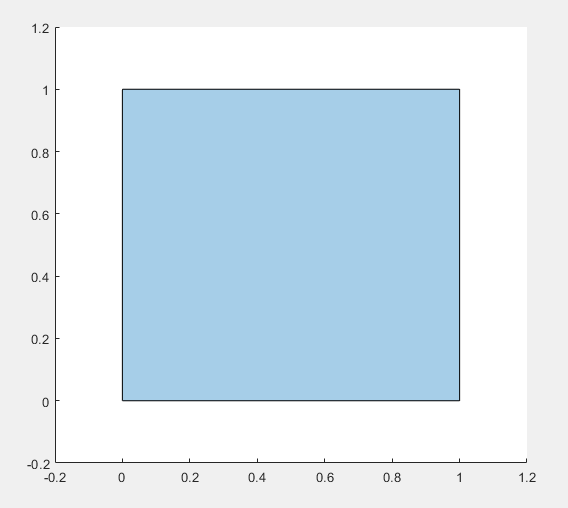
函数可创建由二维顶点定义的多边形,并返回具有描述其顶点、实心区域和孔的各种属性的 polyshape 对象。例如,pgon = polyshape([0 0 1 1],[1 0 0 1]) 将创建由四个点 (0,1)、(0,0)、(1,0) 和 (1,1) 定义的实心正方形。
pgon = polyshape( 从由 x 坐标向量和对应的 y 坐标向量定义的二维顶点创建 x,y)polyshape。x 和 y 的长度必须相同,且至少要有三个元素。

pgon = polyshape([0 0 1 1],[1 0 0 1]); figure(4) plot(pgon)
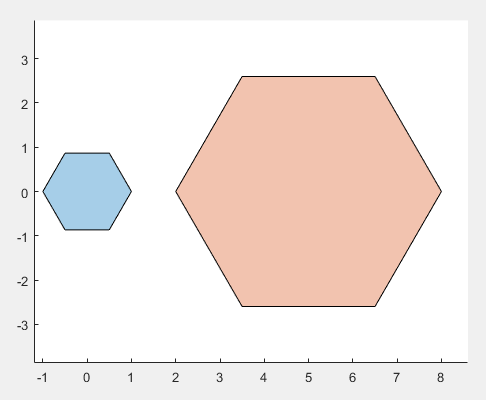
nsidedpoly 正多边形
pgon = nsidedpoly(n,Name,Value)

pgon1 = nsidedpoly(6); pgon2 = nsidedpoly(6,'Center',[5 0],'SideLength',3); figure(4) plot([pgon1 pgon2]) axis equal
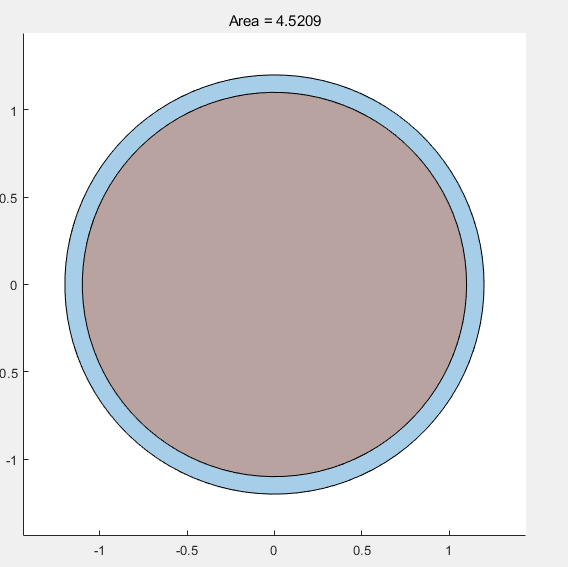
polyarea 计算多边形的面积

L = linspace(0,2.*pi,100); xv = 1.2*cos(L)'; yv = 1.2*sin(L)'; xx=1.1*cos(L)'; yy=1.1*sin(L)'; AA=polyshape(xv,yv); AAA=polyshape(xx,yy); plot(AA); hold on; plot(AAA); title(['Area = ' num2str(A)]) axis image A = polyarea(xv,yv) %计算面积
inpolygon 位于多边形区域边缘内部或边缘上的点
in = inpolygon(xq,yq,xv,yv) 返回 in,以指明 xq 和 yq 所指定的查询点是在 xv 和 yv 定义的多边形区域的边缘内部还是在边缘上
[ 还返回 in,on] = inpolygon(xq,yq,xv,yv)on 以指明查询点是否位于多边形区域的边缘。

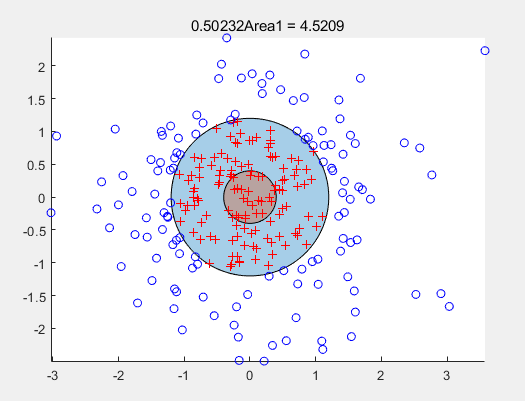
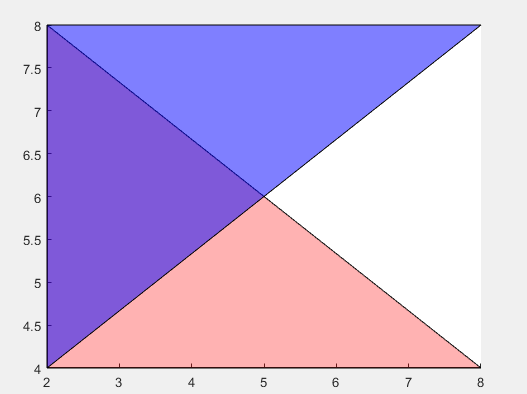
clc,clear all; L = linspace(0,2.*pi,100); xv1 = 1.2*cos(L)'; yv1 = 1.2*sin(L)'; xv2=0.4*cos(L)'; yv2=0.4*sin(L)'; Round1=polyshape(xv1,yv1); Round2=polyshape(xv2,yv2); Round1Area = polyarea(xv1,yv1) Round2Area = polyarea(xv2,yv2) rng default %恢复matlab启动时默认的全局随机流 xq = randn(250,1); %随机生成250个正态分布点 yq = randn(250,1); %随机生成250个正态分布点 in = inpolygon(xq,yq,xv1,yv1); % numel(xq(in))查看在几何体内部的数量 figure(4) plot(Round1); %画第一个圆 hold on; plot(Round2); %画第二个圆 plot(xq(in),yq(in),'r+') % 标记在内部的点 plot(xq(~in),yq(~in),'bo') % 标记在外部的点 hold off title(['Area1,Area2 = ' num2str(Round1Area),num2str(Round2Area)]) axis equal axis image

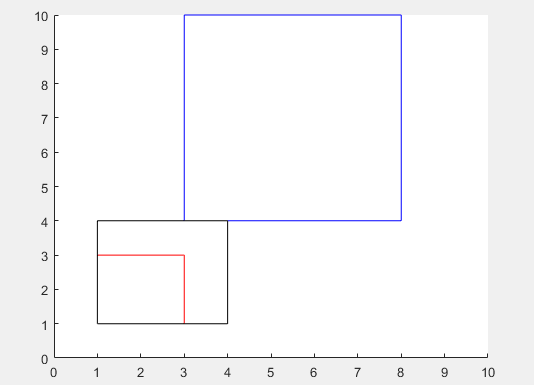
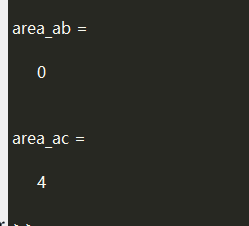
axes('xlim',[0 10],'ylim',[0 10]) a=[1 1 2 2]; b=[3 4 5 6]; c=[1 1 3 3]; figure rectangle('position',a,'EdgeColor', 'r'); rectangle('position',b,'EdgeColor', 'b'); rectangle('position',c,'EdgeColor', 'k'); area_ab = rectint(a,b) area_ac = rectint(a,c)
area = rectint(A,B) 返回位置向量 A 和 B 指定的矩形的交叉区域。
如果 A 和 B 分别指定一个矩形,则输出 area 为标量。
A 和 B 还可以是矩阵,其中每行是一个位置向量。area 是一个矩阵,为 B 指定的所有矩形提供 A 指定的所有矩阵的交叉区域。即,如果 A 是 n×4 并且 B 是 m×4,则 area 是 n×m 矩阵,其中 area(i,j) 是 A 的第 i 行和 B 的第 j 行指定的矩形的交叉区域。

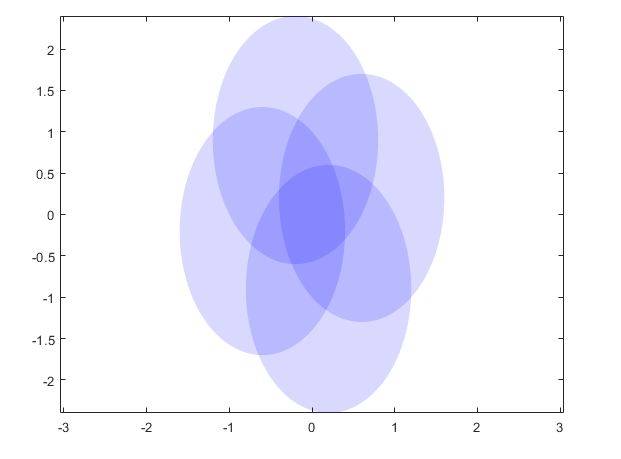
a=1;b=1.5;d=0:360; x=a*cosd(d); y=b*sind(d); figure(1),cla patch(x+0.6,y+0.2,'b','edgecolor','none','facealpha',0.15);%不透明度0.15 patch(x-0.6,y-0.2,'b','edgecolor','none','facealpha',0.15);%不透明度0.15 patch(x-0.2,y+0.9,'b','edgecolor','none','facealpha',0.15);%不透明度0.15 patch(x+0.2,y-0.9,'b','edgecolor','none','facealpha',0.15);%不透明度0.15 axis equal box on; set(gcf,'color','w');

v1 = [2 4; 2 8; 8 4]; f1 = [1 2 3]; figure patch('Faces',f1,'Vertices',v1,'FaceColor','red','FaceAlpha',.3); v2 = [2 4; 2 8; 8 8]; f2 = [1 2 3]; patch('Faces',f2,'Vertices',v2,'FaceColor','blue','FaceAlpha',.5);
boundary 二维或三维空间内的一组点的边界

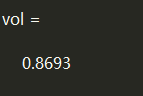
x = gallery('uniformdata',3000,1,1); y = gallery('uniformdata',3000,1,10); plot(x,y,'k.') xlim([-0.3 1.2]) ylim([-0.3 1.2]) k = boundary(x,y); %返回一个表示包围点 (x,y) 的单个相容二维边界的点索引向量。收缩因子为1 hold on; line(x(k),y(k),'color','b'); j = boundary(x,y,0.01); %收缩因子为0.1 最大为1 越大包裹性越紧 line(x(j),y(j),'color','r'); [~, vol] = boundary(x,y); %包围点形成的形状的体积 或 面积 axis equal; vol %返回 包围的体积或者面积
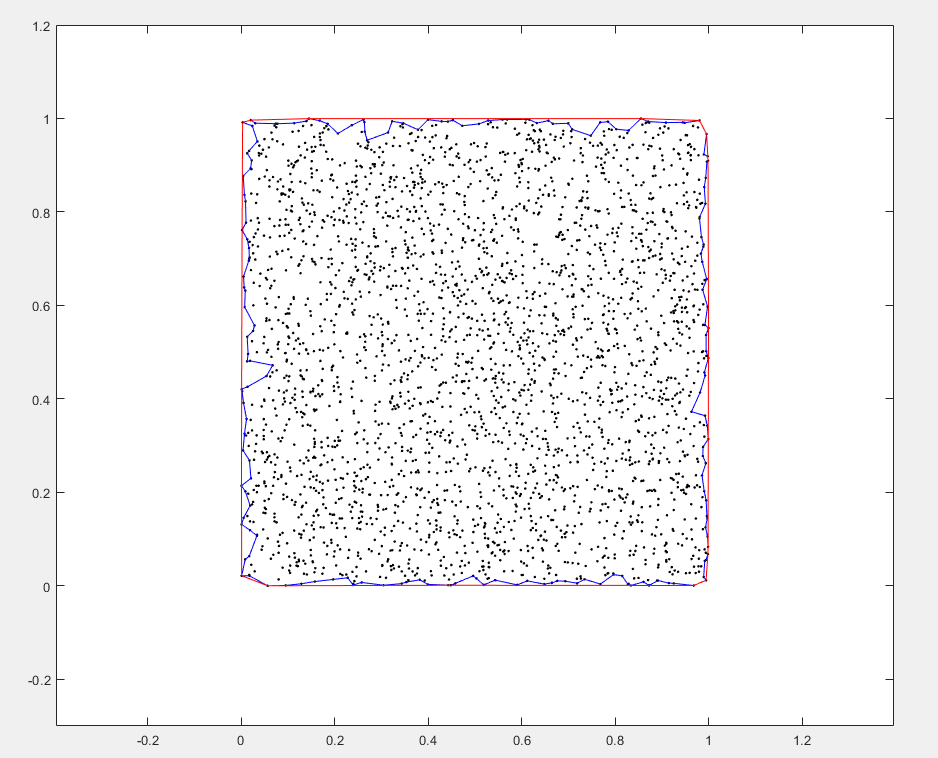
[~, vol] = boundary(x,y); %包围点形成的形状的体积
axis equal;
vol 可以输出二维平面 各个点包围的面积

P = gallery('uniformdata',30,3,5); subplot(1,2,1); plot3(P(:,1),P(:,2),P(:,3),'.','MarkerSize',10) axis equal; grid on k = boundary(P); hold on subplot(1,2,2); trisurf(k,P(:,1),P(:,2),P(:,3),'Facecolor','red','FaceAlpha',0.1) %收缩因子默认0 [~, vol] = boundary(P); %包围点形成的形状的体积 axis equal; vol %体积
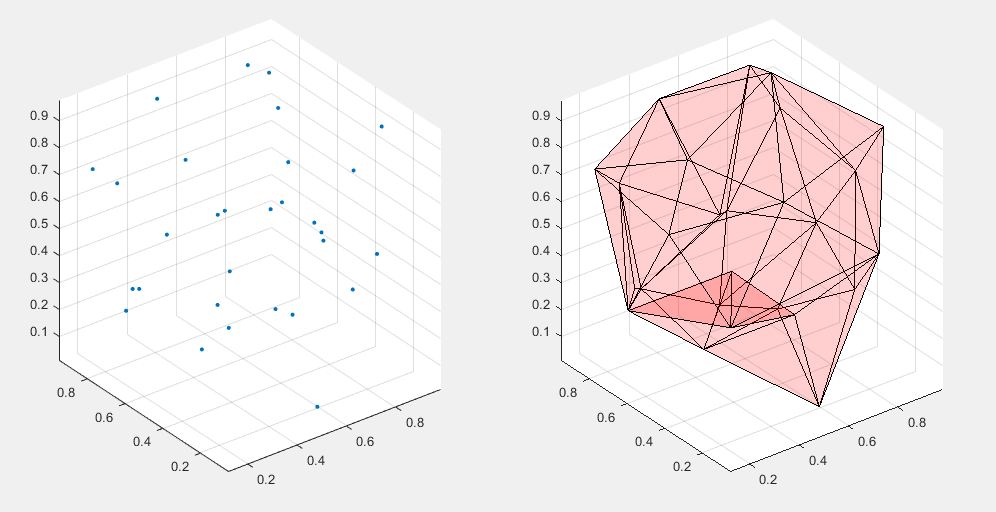
[~, vol] = boundary(P); vol 返回体积
convhull 凸包

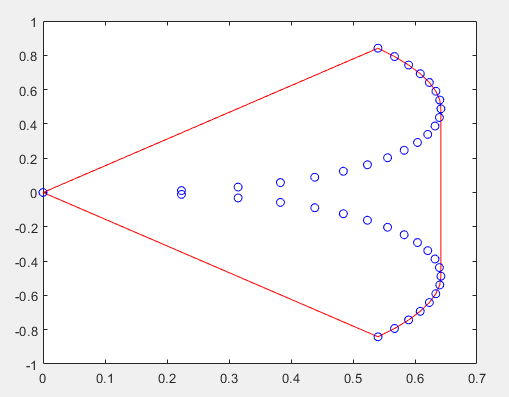
xx = -1:.05:1; yy = abs(sqrt(xx)); [x,y] = pol2cart(xx,yy); k = convhull(x,y); plot(x(k),y(k),'r-',x,y,'bo')
alphaShape 依据二维和三维中的点构建的多边形和多面体

th = (pi/12:pi/12:2*pi)'; x1 = [reshape(cos(th)*(1:5), numel(cos(th)*(1:5)),1); 0]; y1 = [reshape(sin(th)*(1:5), numel(sin(th)*(1:5)),1); 0]; x = [x1; x1+15]; y = [y1; y1]; subplot(1,2,1) plot(x,y,'.') axis equal subplot(1,2,2) shp = alphaShape(x,y); %默认 alpha 半径可生成带不规则边界的 alpha 形状。 shp.Alpha = 2.5; % 要更好地捕获点集边界,请尝试更大的alpha 半径。 plot(shp) axis equal
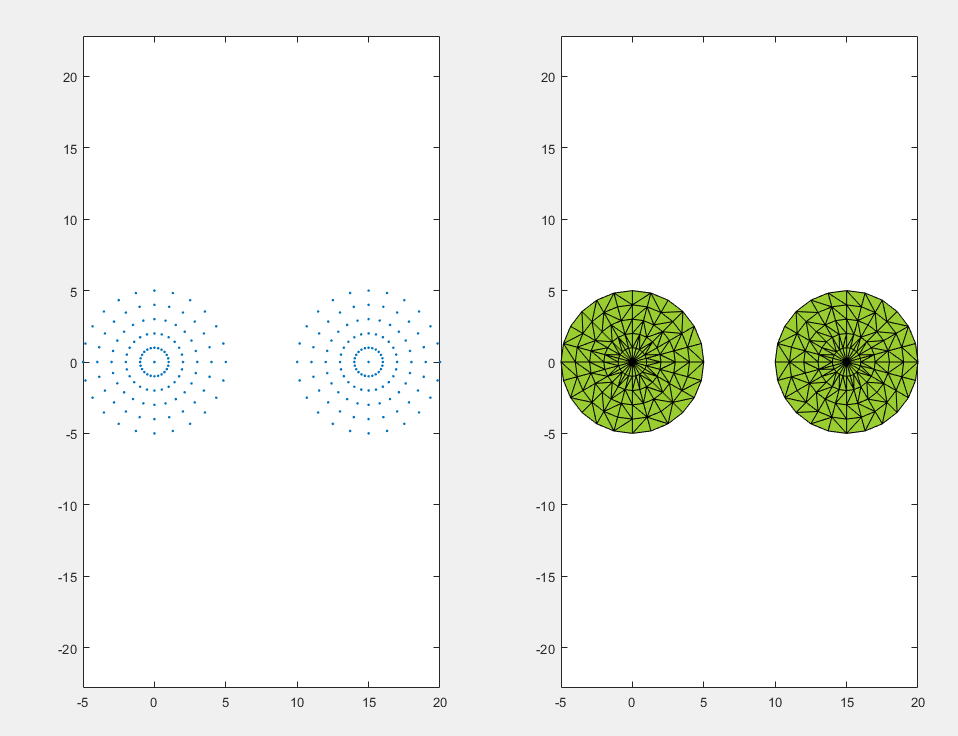
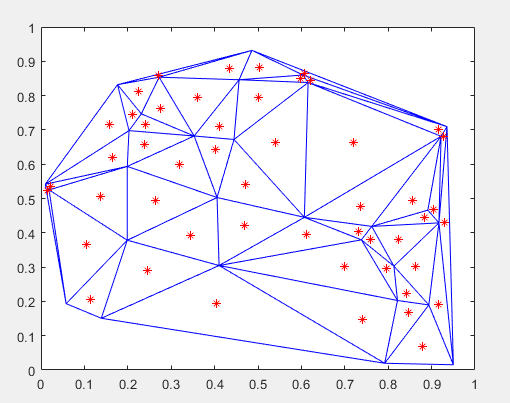
delaunayTriangulation
使用 delaunayTriangulation 对象可以基于一组点创建二维或三维 Delaunay 三角剖分。对于二维数据,您也可以指定边约束。

P = gallery('uniformdata',[30 2],0); DT = delaunayTriangulation(P); IC = incenter(DT); triplot(DT) %绘制 Delaunay 三角剖分 hold on plot(IC(:,1),IC(:,2),'*r')