惊奇的发现躺在任务计划里几个月的“(P3177)树上染色”变成蓝题了,既然前几天清北学堂提到这题了,那就看一眼。(众所周知,洛谷任务计划是个栈)
本人十分不擅长(DP),尤其像什么树形背包题,尤其是为啥看上去 (n^3) 的复杂度都说是 (n^2) 的,让我十分害怕,因为别人说的经典句子什么"两个点只会在 (LCA) 处合并",这 (nm) 我怎么总感觉是错的啊。
我曾经以为的优化就是指枚举到子树大小与父亲的 (min) 即可,但很长时间以来都被这个玄学的复杂度所困扰,因为这明显一条链可以卡的掉啊,换上链的复杂度是 (n*(n-1)+(n-1)*(n-2)+(n-2)*(n-3)...+2*1),难道这东西确实是 (n^2) 的?(雾。
我信你个鬼,很明显不是啊~。。我个大彩笔。
那么产生分歧的地方很明显:
我做的时候是将整个树的 (siz[rt]) 去与子树的 (siz[v]) 进行合并,它张这样:
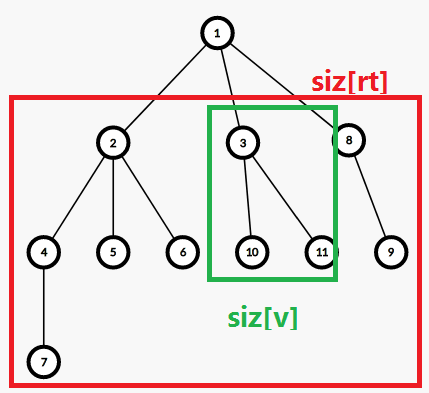
大家都说只会在(LCA)处合并,相互产生贡献的肯定是像下面这样的:
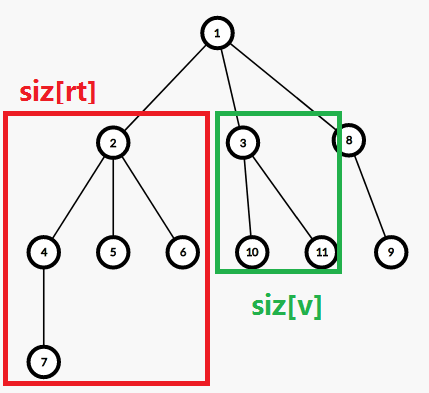
每个子树都不交叉,它们的(LCA)都是这棵子树的根,设这个子树的第 (i) 个儿子大小为 (siz[i]),那么每次的复杂度就是
(siz[2]*siz[1]+siz[3]*(siz[2]+siz[1])+siz[4]*(siz[3]+siz[2]+siz[1])+...+siz[n]*(siz[n-1]+siz[n-2]+...+siz[1]))
(=sumlimits_{i=1}^n sumlimits_{j=1}^n siz[i]*siz[j] (i!=j))
就是两两子树相乘。既然每个点当根的复杂度不好证,那么就考虑将每个 (siz) 看做这个子树中的每个点,看整棵树中所有的点对复杂度的贡献。
考虑到子树不交叉,那么这棵树的任意两个点对背包进行更新答案时,肯定要保证这两个点:1、都在当前根的子树中;2、不在当前根的同一个儿子子树中。那么显然,这个根是它俩的 (LCA),是这个意思。写的好的话复杂度基本 (n^2) 不多不少。
所以,为了保证 (n^2) ,我们不能提前处理出所有子树的大小,而是边合并边做背包。
关于树形背包的心路历程呢还得看这道题,就是刚刚从任务计划里出来的(从栈底开了个洞钻出来的)这道(P3177)。
有些树形背包题数据范围是 (n^3) 的,不用考虑这些。这题是 (n^2),而且最近洛谷放进去一个加强数据,果然就是一条链,卡掉了一部分题解。
由于数据加强了,过会儿考虑发给洛谷一个题解,咕值快要掉出前100了,qwq。
题意:
给你一颗 (n) 个点带边权的树,要你将 (k) 个点涂成黑色,其余点为白色,整棵树的价值为任意两个黑点的距离之和,加上任意两个白点的距离之和。((0leq kleq nleq 2000))
一看数据范围就很友善(雾,显然没有 (O(n)) 的算法或者其他神奇的乱搞,所以考虑 (dp),(f[i][j])表示 (i) 子树中选了 (j) 个黑点的最。。。(愣住)。发现子树最优解并不独立,它还会与其他点产生贡献,我们需要考虑全局最优。
既然任意两点之间的贡献很难处理,那我们将所有的贡献转移到边上,突然就发现简单轻松了许多:一条边的贡献为两边的黑点数相乘加上白点数相乘。
而且恰好,在枚举子树内有多少黑点时,我们同样知道子树外有多少黑点(因为整棵树正好要选 (k) 个),还知道子树内白点个数,以及子树外白点个数,这条连接当前根与儿子的边的贡献就可以算出来了。
考虑这样做的可行性,因为一条边我们已经固定了这棵子树内黑点的个数,而外面的黑点无论在什么位置,这条边的价值是不变的。所以我们放心地让每棵子树内的边权和最大,最后一定会是最优解。
于是来到了树形背包的环节,接下来是几分钟就能写好的代码:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
int n,m;
struct E{ int to,we; };
vector <E> e[2333];
int siz[2333];
int f[2333][2333];
inline int read() {
int sum = 0, f = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') f = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * f;
}
inline int MIN(int aa,int bb) { return aa<bb?aa:bb; }
void DFS(int u,int fa) {
siz[u] = 1;
for(int i=0;i<e[u].size();i++) {
int v = e[u][i].to;
if(v==fa) continue;
DFS(v,u);
siz[u] += siz[v];
}
f[u][0] = f[u][1] = 0;
for(int i=0;i<e[u].size();i++) {
int v = e[u][i].to, w = e[u][i].we;
if(v==fa) continue;
for(int j=MIN(siz[u],m); ~j; --j) {
for(int k=0; k<=MIN(siz[v],j); k++) {
int val = w * ( k*(m-k) + (siz[v]-k)*(n-m-siz[v]+k) );
f[u][j] = max( f[u][j], f[u][j-k]+f[v][k]+val );
}
}
}
}
int main () {
memset(f,-0x3f,sizeof(f));
int x,y,z;
n = read(); m = read();
for(int i=1;i<n;i++) {
x = read(); y = read(); z = read();
e[x].push_back( (E){y,z} );
e[y].push_back( (E){x,z} );
}
DFS(1,0);
cout<<f[1][m];
return 0;
}
如果树形背包不太熟练的人,像我,很有可能发现自己的代码交上去WA了或TLE了,然而这种题就算下载数据再小也是基本没法调试的,建议WA或TLE的同学看看下面这三条:
1、由于树形背包是已经滚掉一维的(枚举到当前第几个儿子),我们枚举j要倒着枚举,因为我们一直用小的 (j) 更新大的 (j) ,如果先更新了小的 (j) ,可能会出现重复选取的情况。
2、再个就是枚举 (v) 中的黑点 (k) ,直觉上来看按说看似这层正着倒着都行,因为 (j) 是倒着枚举的,比 (j) 大的状态是已经合并了 (v) 子树的(上一层状态),比 (j) 小的状态一定是没有合并 (v) 子树的(本层状态),用 (f[u][j-k]) 去更新 (f[u][j]),肯定是用没有合并的状态去更新合并后的状态。但是,这题得考虑个东西:当 (k=0) 的情况,会出现这么一种转移:
(f[u][j]=max(f[u][j],f[u][j]+f[v][k]+val))。
你以为你的 (f[u][j-k]) 是上一层的状态?它可能已经被更新成这一层了!所以 (f[u][j]) 确实需要先转移一下,否则被新的一层更新掉之后,你就再也找不到这个状态了,而且不光找不到,还会把本层的 (f[u][j]) 进行重复转移,与上述第一条的原理类似,相当于重复选取,只不过看上去 (k=0) 没有选黑点,但是白点也是有贡献的啊!
所以,在做DP题尤其像为了这种省空间的背包题时,要滚掉一维的话细节是要仔细考虑的,否则丢掉上一层状态和同层状态互相转移是经常会发生的,如果实在认怂,就开成 (f[u][j][0/1]) 这样就不用担心上述 1 与 2 的枚举顺序了,不过貌似也没人这么做。
3、洛谷新增加了一组数据,好多份题解都TLE了,但不代码他们代码就是错的,因为树形背包题随机数据上述写法是很快的。但是有一种数据可以卡掉:一条链。如果每次j都枚举到 (siz[u]) 的话,复杂度确实是有问题的,为了让复杂度成为树形背包中常说的那句:“任意两个点在其LCA处合并”,我们不能提前处理出子树的 (siz),而是边做背包边合并,这样可以保证两个点会在不同的儿子子树之间合并。
这种写法由于是将做差转移改为了求和转移,我们也不用考虑 (f[u][j-k]) 的状态不存在的情况了,就不用赋初值了。仿佛更好写了。
下面是AC代码:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
int n,m;
struct E{ int to,we; };
vector <E> e[N];
int siz[N];
int f[2333][2333];
inline int read() {
int sum = 0, f = 1; char c = getchar();
while(c<'0' || c>'9') { if(c=='-') f = -1; c = getchar(); }
while(c>='0'&&c<='9') { sum = sum * 10 + c - '0'; c = getchar(); }
return sum * f;
}
inline int MIN(int aa,int bb) { return aa<bb?aa:bb; }
void DFS(int u,int fa) {
siz[u] = 1;
for(int i=0;i<e[u].size();i++) {
int v = e[u][i].to, w = e[u][i].we;
if(v==fa) continue;
DFS(v,u);
for(int j=siz[u]; ~j; --j) {
if(m<j) continue;
for(int k=MIN(m-j,siz[v]); ~k; --k) {
int val = w * ( (n-m-siz[v]+k)*(siz[v]-k) + (m-k)*k );
f[u][j+k] = max( f[u][j+k], f[u][j] + f[v][k] + val );
}
}
siz[u] += siz[v];
}
}
int main () {
int x,y,z;
n = read(); m = read();
for(int i=1;i<n;i++) {
x = read(); y = read(); z = read();
e[x].push_back( (E){y,z} );
e[y].push_back( (E){x,z} );
}
DFS(1,0);
cout<<f[1][m];
return 0;
}
如果是像我这样树形背包不熟练的同学,建议将每次(WA)的原因找出来,而不是乱改了一番(AC)了之后就走了。否则如果理解不是很清晰的话(这种题细节还是蛮多的说),下次再遇到此类的题,一遍(AC)就像冒险一样。