BZOJ-3495 前缀优化建图2-SAT

题意：有n个城镇被分成了k个郡，有m条连接城镇的无向边。要求给每个郡选择一个城镇作为首都，满足每条边至少有一个端点是首都。

解法：以前没学过，参考https://blog.csdn.net/linkfqy/article/details/76242377的解法，涨姿势了。首先普通的建图，对于一个国家只能有一个首都，朴素的想法是如果选一个点为首都那么这个国家其他点都不能选，这样建图是n^2的显然会爆空间加超时。这里用到一种加前缀优化建图的技巧，主要是我们观察朴素建图有很多重复的浪费边，像在这个首都里选i点那么会从i连向(1,2...i-1,i+1,...n)的不选边，如果选i+1点就会向(1,2...i,i+2...n)连不选边，其实这两堆边除了i和i+1有些许不同，连向其他的边都是一样的，十分浪费。于是我们像用前缀来表示从而优化建图。

用u表示选i点，u'表示不选i点，U表示选u点前缀的某一个，U'表示不选u的前缀。那么仔细思考连边：

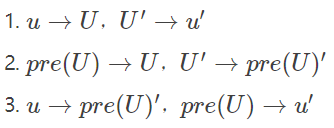
然后做2-SAT就行了。

细节详见代码：

#include<bits/stdc++.h>
using namespace std;
const int N=4e6+10;
int n,m,k,dfs_clock=0,scc_cnt=0;
int pre[N],dfn[N],low[N],c[N];

int cnt=1,head[N<<1],nxt[N<<1],to[N<<1];
void add_edge(int x,int y) { 
    nxt[++cnt]=head[x]; to[cnt]=y; head[x]=cnt;
}

int top=0,S[N],ins[N];
void tarjan(int x) {
    low[x]=dfn[x]=++dfs_clock;
    ins[x]=1; S[++top]=x;
    for (int i=head[x];i;i=nxt[i]) {
        int y=to[i];
        if (!dfn[y]) {
            tarjan(y);
            low[x]=min(low[x],low[y]);
        } else if (ins[y]) low[x]=min(low[x],dfn[y]);
    }
    if (dfn[x]==low[x]) {
        int y; ++scc_cnt;
        do {
            y=S[top--]; ins[y]=0;
            c[y]=scc_cnt;
        } while (x!=y);
    }
}

int main()
{
    cin>>n>>m>>k;
    //u->4x:点x首都，u'->4x+1:点x不首都，U->4x+2:前缀x首都，U'->4x+3:前缀x不首都 
    for (int i=1;i<=m;i++) {
        int x,y; scanf("%d%d",&x,&y);
        add_edge(4*y+1,4*x); add_edge(4*x+1,4*y);  //一条边两个点必有一个首都 
    }
    for (int i=1;i<=k;i++) {
        int t,x,lst=0; scanf("%d",&t);
        for (int j=1;j<=t;j++) {
            scanf("%d",&x);
            pre[x]=lst; lst=x;
        }
    }
    for (int i=1;i<=n;i++) {  //前缀优化建图 
        add_edge(4*i,4*i+2);  //u->U
        add_edge(4*i+3,4*i+1);  //U'->u'
        if (pre[i]) {  
            add_edge(4*pre[i]+2,4*i+2);  //Upre[x]->U
            add_edge(4*i+3,4*pre[i]+3);  //U'->U'pre[x]
            add_edge(4*i,4*pre[i]+3);  //u->U'pre[x]
            add_edge(4*pre[i]+2,4*i+1);  //Upre[x]->u'
        }
    }
    
    for (int i=1*4;i<=n*4+3;i++)
        if (!dfn[i]) tarjan(i);
    for (int i=1*4;i<=n*4+3;i++)
        if (c[i]==c[i^1]) return puts("NIE"),0;
    puts("TAK");    
    return 0;
}