总结:
这一次,最后一次,还是不行啊。
文件操作方面:没有FCLOSE,血的教训。
考场复盘:
首先一二题没什么好讲的,秒切。但是第三题由于一开始看出来是完全背包,但是好像又不是,去年又有摆渡车阴影,就先跳到了第四题。感觉还不错。但是最后还是翻车了。
先是自己做,打了个BFS过了1,2测试点,但是大数据没有输出。发现波动的规律就开始思考奇偶性,很快想到了最短路并且打完了。但其实算法里面存在极其多的纰漏。直接去的大数据,但其实小数据都做错了。大数据大部分吻合,少部分不吻合。一直改一直改下来肉眼看不出差别了,但是数据又太多,现场学了好久的cmdFC比较,下一次一定要能灵活运用才行。之后回到第三题,不会就是不会,开始骗分。
最后回到家测出来只有两百出头,但是已经没有机会了。只能在提高努力了。fclose。再也不会忘了。
题解
第一题
水题切了。

#include<cstdio> #include<iostream> #include<fstream> #include<algorithm> #include<cstring> using namespace std; int read(){ int res=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){ if(ch=='-')f=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ res=res*10+(ch-'0'); ch=getchar(); } return res*f; } char s[9]; int ans; int main(){ for(int i=1;i<=8;++i){ cin>>s[i]; if(s[i]=='1')ans++; } printf("%d",ans); return 0; }
第二题
模拟一下,用一个数组模拟队列,再加一个标记数组是否使用。切了。

#include<cstdio> #include<iostream> #include<fstream> #include<algorithm> #include<cstring> using namespace std; int read(){ int res=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){ if(ch=='-')f=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ res=res*10+(ch-'0'); ch=getchar(); } return res*f; } int n,w[100005],p[100005],t[100005]; int que[100005],he,ta,ans,vis[100005]; int main(){ n=read(); for(int i=1;i<=n;++i){ w[i]=read(); p[i]=read(); t[i]=read(); while((t[i]-t[que[he]]>45||vis[he]==1)&&he<ta)he++; if(w[i]==0){ ans+=p[i]; que[ta++]=i; } else if(w[i]==1){ for(int j=he;j<ta;++j){ if(p[que[j]]>=p[i]&&!vis[j]){ vis[j]=1; p[i]=0; break; } } ans+=p[i]; } } printf("%d",ans); return 0; }
第三题
思路
这道题,是个完全背包。说他是完全背包,却又逐渐虚玄了起来。
当时看到这道题的时候,主要把我难到的地方是:可以今天买了再等到很多天后再卖。那么着眼于这个问题,如果解决,后面就会通畅许多。
从题面可以得到,一天是可以无限进行交易的,可以买进也可以卖出。如果小伟是一个闲人,他完全可以在这一天之内无限制的买了再卖买了再卖,虽然手中的钱并没有怎么变化。
由这个假想情景可以得出:只需要考虑昨天我买进,今天我卖出,若是后面发现亏了,再买回来就行。基于这个条件,我们只需要每天做一遍完全背包,得到每天能赚的最大值,持续累积就是最终答案。
有了如上的思路就开始进行方程式的推导。
对于当前的这一天i,唯一需要考虑的条件就是这一天手上有多少的金币可以使用。而根据上一段所提到的昨天买今天卖的原则,在这一天手中是没有任何的商品的。也就是说现在手上有钱,继续昨天买今天卖就好。
所以说对于这一天的所有商品进行完全背包,结束后要得到一个用上次剩下的钱在昨天买今天卖的基础上的最大赚钱数。因此,钱是价值,也是容量。
方程式:f[k]=max(f[k],f[k-p[i-1][j]]+p[i][j]-p[i-1][j]);
P[i-1][j]就是在昨天买一件j商品所需要的代价,也就是他的价格。p[i][j]-p[i-1][j]则是今天卖出去减去昨天的价格,也就是价格差,赚的钱。
f[m]则是使用m元能挣到的最大钱数。由于是赚的钱,所以累加到m上面,作为下一次买东西的资本。当n天全部过完了,此时的m,就是答案了
注意点:天数i从2开始,不能从1.因为第一天之前没有东西可以买。

#include<cstdio> #include<iostream> #include<fstream> #include<algorithm> #include<cstring> using namespace std; int read(){ int res=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){ if(ch=='-')f=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ res=res*10+(ch-'0'); ch=getchar(); } return res*f; } int n,t,m,p[105][105],f[100005]; int main(){ t=read();n=read();m=read(); if(t==1)cout<<m; else{ for(int i=1;i<=t;++i){ for(int j=1;j<=n;++j){ p[i][j]=read(); } } for(int i=2;i<=t;++i){ memset(f,0,sizeof(f)); for(int j=1;j<=n;++j){ for(int k=p[i-1][j];k<=m;++k){ f[k]=max(f[k],f[k-p[i-1][j]]+p[i][j]-p[i-1][j]); } } m+=f[m]; } printf("%d",m); } return 0; }
第四题
思路:
这题当时做着还是算比较有手感的。虽然最后做错了,差之毫厘。
一开始,我们可以无脑的打一遍BFS,不过只需要细心看看样例就可以发现,制造过程实在来回波动的。
什么意思呢?具体来说就是:由于我们两个是无向边,我做n阶(n>=2)的工件,你就要做n-1阶,那么我就要做n-2阶。那么于是我现在就要做n-2阶,然后又变成n-4..n-6..n-8直至你我中有一人提供原料。那么可以很简易的得出一个结论:如果n%2==0我就必须提供原料。
那么我传到一号,一号就需要做n-a段的零件。a为我到一号的某条路径长度。那么显而易见的,a越小越好,这样才可以保证n>=a。此时需要跑一遍最短路,但是只是最短路是不行的,因为说了是某条路径,换句话说,只要有一条路径使得n-a为偶数,一号就必须提供原料。那么就需要将奇偶最短路都算出来,一减,一判断就能得出答案。
多余的话:
这道题解析到现在,跑两遍单源点最短路就行。但是。一开始我读题的时候思考到一个问题,如果一号和我根本不存在路径,或者一号要做材料,但一号是个孤儿,没有任何人与他链接呢?很显然,对于第一个问题,最短路初始化是最大值,所以n<a,自动屏蔽情况。但是,面对第二个,则需要加入特判,因为这样是不可能实现的。
分层图解法
这是才学的新内容,并不能理解其中的真谛。但是面对这道题,将原图复制成两份,对于第二个复制出来的图,所有的点全部命名为a‘这样的。如果原图是1连2,那么就改成1连2’,2‘连1。
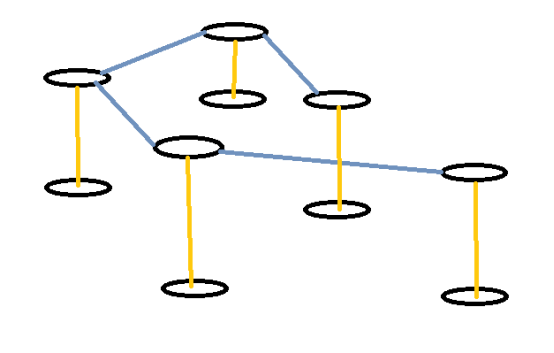
(蓝线为原图,黄线为对应关系)
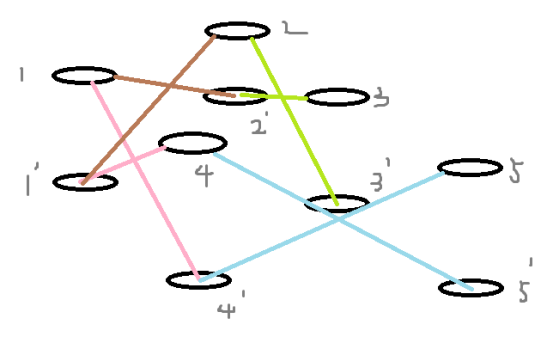
(分层图的建立图示)
这样做有什么好处呢?这两个图拼在一起的话,跑一遍最短路,所有复制图上面的最短路都是奇数最短路,原图上面的最短路都是偶数最短路。这是为什么呢?是因为所有复制图上面的最短路都是由原图(偶数)转化而来的,边权又都=1,所以都是奇数。反之同理。最短由算法保证。
注意点:分层图一定要建成双向的,并且临接表的空间要开到n*4,因为是双层,双边。最后不要光判断奇偶性,还要判断长度是否合适。
分层图代码

#include<cstdio> #include<iostream> #include<fstream> #include<algorithm> #include<cstring> #include<queue> using namespace std; int read(){ int res=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){ if(ch=='-')f=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ res=res*10+(ch-'0'); ch=getchar(); } return res*f; } const int MAXN=200005; int n,m,p; int head[MAXN],ne[2*MAXN],to[2*MAXN],tot; void add(int x,int y){ to[++tot]=y; ne[tot]=head[x]; head[x]=tot; } priority_queue<pair<int,int> > q; bool vis[MAXN]; int dis[MAXN]; void dijistra(){ q.push(make_pair(0,1)); vis[1]=1; memset(dis,127/3,sizeof(dis)); dis[1]=0; while(!q.empty()){ int u=q.top().second; q.pop(); vis[u]=0; for(int i=head[u];i;i=ne[i]){ int v=to[i]; if(dis[v]>dis[u]+1){ dis[v]=dis[u]+1; if(!vis[v]){ vis[v]=1; q.push(make_pair(-dis[v],v)); } } } } } int que[MAXN],s,e; int main(){ n=read();m=read();p=read(); for(int i=1;i<=m;++i){ int a,b; a=read();b=read(); add(a,b+n);add(b,a+n); add(a+n,b);add(b+n,a); } dijistra(); for(int i=1;i<=p;++i){ int a,b; a=read();b=read(); if(a==1&&!head[a])printf("No "); else{ int k; if(b%2)k=dis[a+n]; else k=dis[a]; if(k>b)printf("No "); else if((b-k)%2)printf("No "); else printf("Yes "); } } return 0; }
