方差与协方差

-----------------------------------------------------------------------方差------------------------------------------------------------------

1.衡量一组数据的离散程度，概率论中用方差来度量随机变量和其数学期望（均值）之间的偏离程度。统计中的方差是每个样本值与全体样本值的平均数之差的平方值的平均数。

2.在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式：

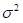 为总体方差，X为变量，μ为总体均值，N为总体例数。

-----------------------------------------------------------------协方差-------------------------------------------------------------------

1.协方差（Covariance）用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

2.期望值分别为E(X)和E(Y)的两个实随机变量X与Y之间的协方差定义为：

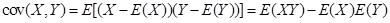
协方差的性质：

（1）Cov(X，Y)=Cov(Y，X)；

（2）Cov(aX，bY)=abCov(X，Y)，（a，b是常数）；

（3）Cov(X₁+X₂，Y)=Cov(X₁，Y)+Cov(X₂，Y)。

由协方差定义，可以看出Cov(X，X)=D(X)，Cov(Y，Y)=D(Y)。

 3.协方差矩阵

分别为m、n个标量元素的列向量随机变量X与Y，这两个变量之间的协方差定义为m×n矩阵.其中X包含变量X1.X2......Xm，Y包含变量Y1.Y2......Yn，假设X1的期望值为μ1，Y2的期望值为v2，在协方差矩阵中(1,2)的元素就是X1和Y2的协方差。

两个向量变量的协方差Cov(X,Y)与Cov(Y,X)互为转置矩阵。