 (2017-08-29 银河统计)
(2017-08-29 银河统计)密度聚类算法,DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法,和K-Means只适用于凸样本集的聚类方法相比,DBSCAN既可以适用于凸样本集,也可以适用于非凸样本集。下面我们就对DBSCAN算法的原理做一个总结。
DBSCAN是一种基于密度的聚类算法,这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本,他们之间的紧密相连的,也就是说,在该类别任意样本周围不远处一定有同类别的样本存在。通过将紧密相连的样本划为一类,这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别,则我们就得到了最终的所有聚类类别结果。DBSCAN算法在大规模数据库上更好的效率。DBSCAN能够将足够高密度的区域划分成簇,并能在具有噪声的空间数据库中发现任意形状的簇。
一、DBSCAN算法基本术语##
DBSCAN是基于一组邻域来描述样本集的紧密程度的,参数(ϵ, MinPts)用来描述邻域的样本分布紧密程度。其中,ϵ描述了某一样本的邻域距离阈值,MinPts描述了某一样本的距离为ϵ的邻域中样本个数的阈值。
2、核心对象:对于任一样本$x_j∈D$,如果其ϵ-邻域对应的$Nϵ(_xj)$至少包含$MinPts$个样本,即如果$|Nϵ(x_j)|≥MinPts$,则$x_j$是核心对象。
3、密度直达:如果$x_i$位于$x_j$的ϵ-邻域中,且$x_j$是核心对象,则称$x_i$由$x_j$密度直达。注意反之不一定成立,即此时不能说$x_j$由$x_i$密度直达, 除非且$x_i$也是核心对象。
4、密度可达:对于$x_i$和$x_j$,如果存在样本样本序列$p_1,p_2,...,p_T$,满足$p_1=x_i,p_T=x_j$, 且$p_t+1$由$p_t$密度直达,则称$x_j$由$x_i$密度可达。也就是说,密度可达满足传递性。此时序列中的传递样本$p_1,p_2,...,p_{T−1}$均为核心对象,因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性,这个可以由密度直达的不对称性得出。
5、密度相连:对于$x_i$和$x_j$,如果存在核心对象样本$x_k$,使$x_i$和$x_j$均由$x_k$密度可达,则称$x_i$和$x_j$密度相连。注意密度相连关系是满足对称性的。
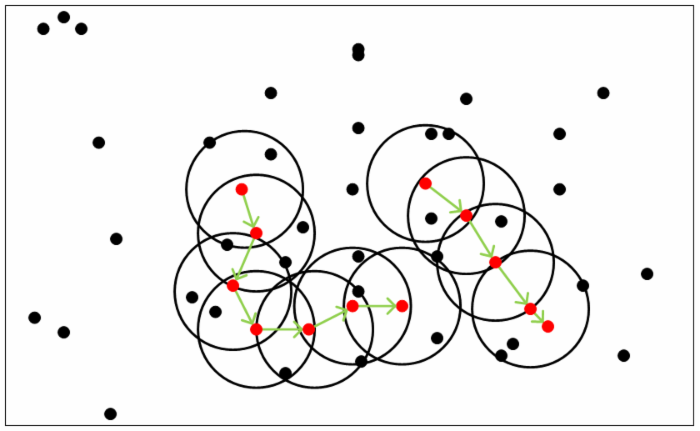
从下图可以很容易看出理解上述定义,图中MinPts=5,红色的点都是核心对象,因为其ϵ-邻域至少有5个样本。黑色的样本是非核心对象。所有核心对象密度直达的样本在以红色核心对象为中心的超球体内,如果不在超球体内,则不能密度直达。图中用绿色箭头连起来的核心对象组成了密度可达的样本序列。在这些密度可达的样本序列的ϵ-邻域内所有的样本相互都是密度相连的。
二、DBSCAN算法定义、思路和流程##
1、算法定义
DBSCAN是基于一组邻域来描述样本集的紧密程度的,参数(ϵ, MinPts)用来描述邻域的样本分布紧密程度。其中,ϵ描述了某一样本的邻域距离阈值,MinPts描述了某一样本的距离为ϵ的邻域中样本个数的阈值。
假设我的样本集是(D=(p_1,p_2,...,p_m)),则DBSCAN具体的密度描述定义如下:
II. 如果p是一个核心对象,q属于p的邻域,那么称p直接密度可达q。
III. 如果存在一条链…..,$p_i$>,满足$p_{_1}=p,p_i=q,p_i$直接密度可达$p_i+1$,则称p密度可达q。
IV. 如果存在o,o密度可达q和p,则称p和q是密度连通的。
V. 由一个核心对象和其密度可达的所有对象构成一个聚类。
2、算法思路
从数据集D中的任意一个点P开始,查找D 中所有关于ϵ-邻域(最小半径)和MinPts(密度阈值)的从P密度可达的点。若P是核心点,则其邻域内的所有点和P同属于一个簇,这些点将作为下一轮的考察对象(即种子点),并通过不断查找从种子点密度可达的点来扩展它们所在的簇,直至找到一个完整的簇;若P不是核心点,即没有对象从P密度可达,则P被暂时地标注为噪声。然后,算法对D 中的下一个对象重复上述过程⋯⋯ 。当所有种子点都被考察过,一个簇就扩展完成了。此时,若D中还有未处理的点,算法则进行另一个簇的扩展;否则,D 中不属于任何簇的点即为噪声。
3、算法流程
三、DBSCAN算法案例##
数据样本如下表(数据表I):
| 序号 | 属性1 | 属性2 |
|---|---|---|
| 1 | 2 | 1 |
| 2 | 5 | 1 |
| 3 | 1 | 2 |
| 4 | 2 | 2 |
| 5 | 3 | 2 |
| 6 | 4 | 2 |
| 7 | 5 | 2 |
| 8 | 6 | 2 |
| 9 | 1 | 3 |
| 10 | 2 | 3 |
| 11 | 5 | 3 |
| 12 | 2 | 4 |
样本散点图如下:
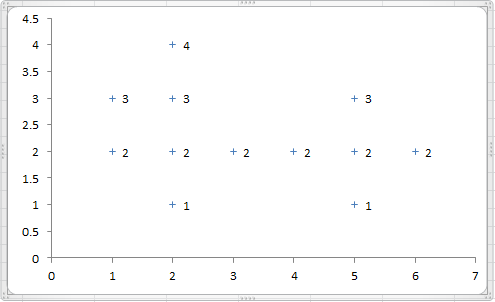
令ϵ = 1,MinPts = 4,试用密度聚类算法对样本进行分类。
样本间欧几里得距离矩阵表如下(数据表II):
| i/j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3 | 1.41 | 1 | 1.41 | 2.24 | 3.16 | 4.12 | 2.24 | 2 | 3.61 | 3 |
| 2 | 3 | 0 | 4.12 | 3.16 | 2.24 | 1.41 | 1 | 1.41 | 4.47 | 3.61 | 2 | 4.24 |
| 3 | 1.41 | 4.12 | 0 | 1 | 2 | 3 | 4 | 5 | 1 | 1.41 | 4.12 | 2.24 |
| 4 | 1 | 3.16 | 1 | 0 | 1 | 2 | 3 | 4 | 1.41 | 1 | 3.16 | 2 |
| 5 | 1.41 | 2.24 | 2 | 1 | 0 | 1 | 2 | 3 | 2.24 | 1.41 | 2.24 | 2.24 |
| 6 | 2.24 | 1.41 | 3 | 2 | 1 | 0 | 1 | 2 | 3.16 | 2.24 | 1.41 | 2.83 |
| 7 | 3.16 | 1 | 4 | 3 | 2 | 1 | 0 | 1 | 4.12 | 3.16 | 1 | 3.61 |
| 8 | 4.12 | 1.41 | 5 | 4 | 3 | 2 | 1 | 0 | 5.1 | 4.12 | 1.41 | 4.47 |
| 9 | 2.24 | 4.47 | 1 | 1.41 | 2.24 | 3.16 | 4.12 | 5.1 | 0 | 1 | 4 | 1.41 |
| 10 | 2 | 3.61 | 1.41 | 1 | 1.41 | 2.24 | 3.16 | 4.12 | 1 | 0 | 3 | 1 |
| 11 | 3.61 | 2 | 4.12 | 3.16 | 2.24 | 1.41 | 1 | 1.41 | 4 | 3 | 0 | 3.16 |
| 12 | 3 | 4.24 | 2.24 | 2 | 2.24 | 2.83 | 3.61 | 4.47 | 1.41 | 1 | 3.16 | 0 |
| MinPts | 1 | 1 | 2 | 4 | 2 | 2 | 4 | 1 | 2 | 3 | 1 | 1 |
密度聚类分析:
II、 样本4密度直达样本为样本1、3、4、5、10;
III、样本7密度直达样本为样本2、6、7、8、11;
IV、样本4的密度直达样本3和样本9密度直达、样本6和样本5密度直达、样本10和样本12密度直达,所有样本4和样本9、6、12密度可达。这样,样本1、3、4、5、9、10、12聚类为一簇(有样本4本身、4个直接可达、2个间接可达样本构成)。样本6和另一个核心对象样本7密度直达,应归为另一个簇;
V、样本7的密度直达样本6和样本5密度直达,样本7和样本5密度可达。但由于样本5和核心对象样本4密度直达,所以样本5属于以样本4为核心对象的簇。
综合上述分析,样本聚类为两个簇{1、3、4、5、9、10、12}和{2、6、7、8、11}。
四、DBSCAN算法API接口##
应用程序接口(API:application programming interface)是一组定义、程序及协议的集合,通过 API 接口实现计算机软件之间的相互通信。API 的一个主要功能是提供通用功能集。程序员通过使用 API 函数开发应用程序,从而可以避免编写无用程序,以减轻编程任务。
基于互联网的应用正变得越来越普及,在这个过程中,有更多的站点将自身的资源开放给开发者来调用。对外提供的API 调用使得站点之间的内容关联性更强。开放是目前的发展趋势,越来越多的产品走向开放。目前的网站不能靠限制用户离开来留住用户,开放的架构反而更增加了用户的粘性。在Web 2.0的浪潮到来之前,开放的API 甚至源代码主要体现在桌面应用上,而现在越来越多的Web应用面向开发者开放了API。
通过开放的API 来让站点提供的服务拥有更大的用户群和服务访问数量。站点在推出基于开放API 标准的产品和服务后,无需花费力气做大量的市场推广,只要提供的服务或应用出色易用,其他站点就会主动将开放API 提供的服务整合到自己的应用之中。同时,这种整合API 带来的服务应用,也会激发更多富有创意的应用产生。开放API 的站点为第三方的开发者提供良好的社区支持也是很有意义的,这有助于吸引更多的技术人员参与到开放的开发平台中,并开发出更为有趣的第三方应用。
银河统计工作室陆续推出数据挖掘、统计随机数及临界值、房地产数据等API接口服务,下面详细介绍DBSCAN算法API接口用法。
1、DBSCAN算法API接口样例及参数解释
I、接口样例
URL:http://api.galaxystatistics.com:8882/?token=098f6bcd4621d373cade4e832627b4f6&type=13&var_name=dbscanMethod&data_str=2,1|5,1|1,2|2,2|3,2|4,2|5,2|6,2|1,3|2,3|5,3|2,4&oEps=1&oMinPts=4
注:在浏览器中运行接口样例字符,可返回上传样本密度聚类结果
II、接口参数说明
API接口域名网址:
http://api.galaxystatistics.com端口号:
8882 # 不同的接口,会使用不同的端口号公共测试用Key:
token=098f6bcd4621d373cade4e832627b4f6数据类型:
type=13 # 不同聚类方法的api接口,采用不同的type值【如:11、12、13】输出变量名:
var_name=hclustMethod # 根据程序需求,自定义变量名称【如:hclustMethod、kmeansMethod、dbscanMethod】模型方法参数:
data_str # 数据字符串
oEps # 邻域半径[eps]
oMinPts # 判断核心点阈值[MinPts]
2、DBSCAN算法API回传数据样例及参数解释
I、回传数据样例(JSON)
var dbscanMethod={"No":[1,3,4,5,9,10,12,2,6,7,8,11],"SType":[1,1,1,1,1,1,1,2,2,2,2,2],"X1":[2,1,2,3,1,2,2,5,4,5,6,5],"X2":[1,2,2,2,3,3,4,1,2,2,2,3]}
II、回传数据参数说明
回传数据变量名称:
dbscanMethod #由接口参数var_name指定样本序号:
No # 按聚类类别排序聚类类别:
SType #为数组对象数据列1:
X1 # 样本变量1数组数据列2:
X2 # 样本变量2数组五、DBSCAN算法API接口运用##
注:按格式输入样本数据,设置适当核半径和核心点阈值,点击“密度聚类列表”,自动按DBSCAN算法API接口格式递交数据,并解析回传数据、用列表展示聚类分析结果
核半径和核心点阈值的设置对DBSCAN算法聚类结果影响非常大。如果核心点阈值设置的偏大、或核半径偏小,则没有核心对象,所有样本将被判别为孤立点(分类为0);核心点阈值设置的偏小、或核半径偏大,则核心对象多,样本容易被并为同类、甚至所有样本被聚为一类。
在DBSCAN算法API接口运用模板中,可以试着将核心点阈值改为3、5、6观察密度聚类效果。也可以将核半径改为0.5、2观察聚类效果。
关于R聚类内容参见银河统计之聚类分析 - 用R构建Shiny应用程序