说明
本文源自作者读研期间的一份作业报告,主要基于建立时间、保持时间等时间约束参数推导时序分析公式,并通过实验进行验证。
因时间久远,某些实验数据和理论推导可能存在缺失,且难以回忆。若对读者造成理解困难,还请见谅~
相关实验参见以下两篇文章:
采用流水线技术实现8位加法器
Stratix内嵌存储器测试报告
一 基本概念
建立时间(SetUp Time, tsu):触发器在有效时钟沿来到前,其数据输入端的数据必须保持不变的时间;
保持时间(Hold Time, th):触发器在有效时钟沿来到后,其数据输入端的数据必须保持不变的时间。
输入信号应提前时钟上升沿(如上升沿有效)tsu时间到达芯片,这个tsu就是建立时间。如果建立时间和/或保持时间不够,数据将不能在这个时钟上升沿被打入触发器。如下图所示:
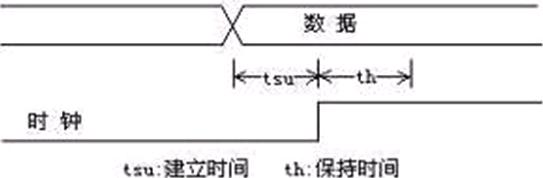
图1 建立时间与保持时间
设时钟上升沿位置为t,则数据最短持续时间段为(t – tsu) ~(t + th)。
补充一点,Quartus里定义tsu、th为:
|
tsu = <pin to register delay> + <micro setup delay> - <clock to destination register delay> th = <clock to destination register delay> + <micro hold delay> - <pin to register delay> |
可知,对于特定的路径,tsu + th = MicrotSU + MicrotH为常数,这也就是数据最短持续时间。其中,MicrotSU/MicrotH指触发器内部固有建立/保持时间,典型值一般小于1ns。
注意,文中建立时间和保持时间均针对时钟而言,在进行时序约束时所指的就是这种;而有些书籍中建立时间和保持时间的概念针对信号而言,所指对象不同,分析结论可能完全相反,请勿混淆。
二 时序分析
2.1 实验一非流水线加法器
打开adder_nonpipe.tan.rpt或Processing->Compilation Report时序分析报告,简化如表1所示:
表1 8位加法器(非流水线/FPGA)时序分析之简表
|
Type |
Actual Time |
From |
To |
From Clock |
To Clock |
|
Worst-case tsu |
3.391ns |
inb[1] |
tempb[1] |
-- |
enable |
|
Worst-case tco |
8.291ns |
sum[4]~reg0 |
sum[4] |
enable |
-- |
|
Worst-case th |
-2.399ns |
ina[2] |
tempa[2] |
-- |
enable |
|
Clock Setup: 'inclk' |
period=2.369ns* |
tempb[0] |
sum[7]~reg0 |
enable |
enable |
注:
- ..ns* 对应fmax=422.12MHz,实际时钟周期为10ns,占空比为1:1。
- tco: from clock "enable" to destination pin "sum[4]" through register "sum[4]~reg0"
- tsu取最大值,得数据最前端(ina 8路并不同步);th取绝对值最小者,得数据最末端。
实际最大建立时间和最小保持时间如表2所示:
表2 8位加法器(非流水线/FPGA)时序分析之tsu与th
|
Actual Maximum tsu |
Actual Minimum th |
From |
To |
第一周期内数据位置 |
|
3.166ns |
-3.056ns |
cin |
tempc |
1.834ns ~ 1.944ns(高) |
|
3.138ns |
-2.399ns** |
ina[n] (n=0..7) |
tempa[n] |
1.862ns ~ 2.601ns |
|
3.391ns** |
-2.550ns |
inb[n] (n=0..7) |
tempb[n] |
1.609ns ~ 2.450ns |
注:..ns**为worst-case情况下的tsu/th时间。
初始化波形如图2所示:

图2 8位加法器(非流水线/FPGA)时序分析之初始波形
仿真结果如图3所示:
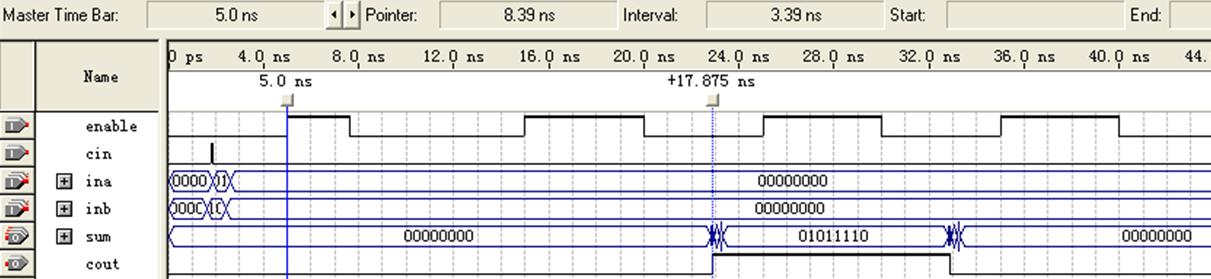
图3 8位加法器(非流水线/FPGA)时序分析之仿真图
注意:
1. 对于某些输入数据,cin、ina、inb可以更“窄”。如:
cin: 1.844ns ~ 1.850ns
ina: 1.948ns ~ 2.601ns
inb: 1.619ns ~ 2.450ns
结果也正确,但并不能保证对于所有输入,输出均正确。
红色ns时间不可越界,时间精度为0.001ns。如cin取1.845ns ~ 1.944ns时,输出不正确。
所以,对于建立时间/保持时间确定的数据时间段为(t – tsu) ~(t + th),宜宽不宜窄。
2. 图3中第一个时钟上升沿为5.0ns,下降沿为7.632ns(原时钟下降沿在10ns处)。当时钟下降沿设为7.632ns之前(如7.631ns)时,输出数据正确,但却延迟了两个周期,相当于第二个时钟周期内并未采到数据,直到第二个时钟上升沿到来时才采样输出。不知道为什么会这样。不过,这种脉宽不同的时钟在实际中似乎并无意义。时钟脉宽可以非常窄,但是各个脉宽不同的话,输出不可预料。
2.2 altsyncram测试实验
altsyncram宏单元结构如图4所示:

图4 altsyncram宏单元结构
此处给出宏单元结构,是因为我在做仿真时序分析时,想当然地认为outclk对输入地址和数据采样并输出(读出)。其实图4中清楚地表明,只有inclk上升沿采样锁存读/写地址和数据,经过一段延时后由outclk上升沿触发输出——outclk的功能类似读使能信号!
时序编译报告如表3所示:
表3 altsyncram读写测试时序分析之简表
|
Type |
Actual Time |
From |
To |
From Clock |
To Clock |
|
Worst-case tsu |
3.523ns |
addr_a[1] |
porta_address_reg1 |
-- |
inclk |
|
Worst-case tco |
7.818ns |
altsyncram|q_a[5] |
q_a[5] |
outclk |
-- |
|
Worst-case th |
-2.346ns |
data_b[7] |
portb_datain_reg0 |
-- |
inclk |
|
Clock Setup: 'inclk' |
period=3.438ns* |
porta_datain_reg7 |
porta_memory_reg7 |
inclk |
inclk |
注:
1. ..ns* 对应fmax=290.87MHz,实际时钟周期为8ns,占空比为1:1。
2. tco: from clock "outclk" to destination pin "q_a[*]" through memory "altsyncram0: inst|altsyncram: altsyncram_component|altsyncram_8982: auto_generated|q_a[*]"
实际最大建立时间和最小保持时间如表4所示:
表4 altsyncram读写测试时序分析之tsu和th
|
Actual Maximum tsu |
Actual Minimum th |
From |
To |
To Clock |
|
3.523ns** |
-2.626ns |
addr_a[n] (n=0..7) |
porta_address_regn |
inclk |
|
3.510ns |
-2.400ns |
addr_b[n] (n=0..7) |
portb_address_regn |
inclk |
|
3.429ns |
-2.605ns |
data_a[n] (n=0..7) |
porta_datain_regn |
inclk |
|
3.383ns |
-2.346ns** |
data_b[n] (n=0..7) |
portb_datain_regn |
inclk |
|
2.640ns |
-2.475ns |
wren_a |
porta_we_reg |
inclk |
|
2.825ns |
-2.660ns |
wren_b |
portb_we_reg |
inclk |
注:..ns**为worst-case情况下的tsu/th时间。
如前所述,inclk上升沿采样锁存地址和数据,经过一段延时δ后由outclk上升沿触发输出。δ的最小值近似等于电路内部最小时钟周期,即
|
δmin = Shortest clock path from clock "inclk" to destination memory(2.875ns) + Micro clock to output delay of source(0.420ns) + Micro setup delay of destination(0.131ns) - smallest clock skew(-0.012ns) = 3.438ns |
而从outclk上升沿到输出寄存器输出数据的延时即为tco,即最大延迟为7.818ns(最小延时则为6.906ns)。
仿真结果如图5所示:

图5 altsyncram读写测试时序分析之仿真图
inclk、outclk都是上升沿触发,与持续时间无关(即时钟脉冲可以非常窄)。
此处未考虑极限情况。其实 tsu、th、tco等参数就描述了所谓的“极限读写”,而tco指示了与时钟触发沿对应的输出(比照输入输出时很有用)。
分析b路数据。第n个时钟上升沿用inclk_n/outclk_n表示,数据和地址内容用signal_b'x表示(如data_b为2时表示为data_b'2)。时钟有效沿之后δ时间处称为δ临界点。
当inclk_1来临时,锁入data_b'1和addr_b'1,并在δ临界点之后检测到outclk_2,延时tco时间后输出q_b'1。
当inclk_2来临时,锁入data_b'3和addr_b'3(注意理解tsu和th),并在δ临界点之后检测到outclk_3。但inclk_3也检测到outclk_3,故更新输出寄存器的输入,并延时tco时间后输出q_b'5。这也意味着要达到连续读写无误,必须在inclk_n的δ临界点之后与inclk_n+1的δ临界点之前这段时间内检测到outclk_n。
后续数据分析原理同上。注意,时序分析时必须考虑tsu和th,切忌单看波形想当然。
下面考虑极限读写:
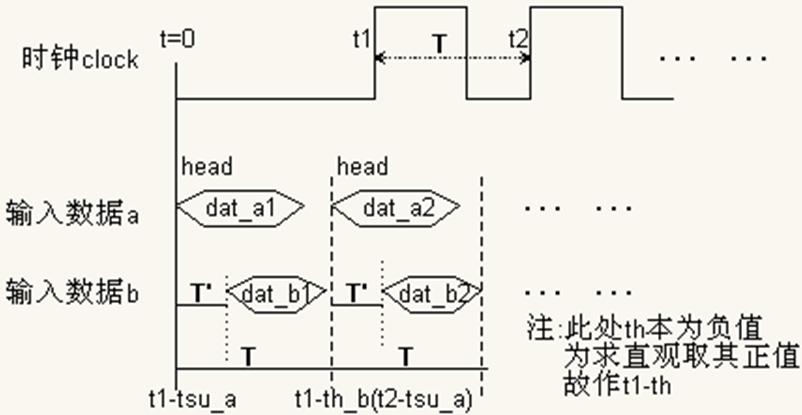
图6 altsyncram极限读写时序示意图
如图6所示,输入数据a和b的持续时间段为由(t – tsu) ~(t - th)确定。
|
T = tsu_a – th_b T' = tsu_a – tsu_b head_a2 = t2 – tsu_a = t1 + T – tsu_a = t1 + tsu_a – th_b – tsu_a = t1 – th_b head_b2 = t2 – tsu_b = t1 + tsu_a – th_b - tsu_b = (t1 – th_b) + (tsu_a – tsu_b) = head_a2 + T' |
在T时间内,数据a的前端(head)最靠前,数据b的末端(back)最靠后。当这个head/back分别是所有输入数据的最前/末端时,就得到了极限情况下(Tmax)的时序图。只有满足这个时序要求,才能达到最快速的正确读写。
极限读写仿真结果如图7所示:

图7 altsyncram极限读写测试仿真图
其中inclk、outclk时钟周期均为1.177ns。按“读写周期指连续进行两次读(或写)操作所需要的最小的最短时间间隔”的定义,取1.177ns为写周期。
仿真波形正确,只是会出现如下警告(影响未知):
Warning: Found clock high time violation at 6.45 ns on register "|altsyncram_test|altsyncram0: inst|altsyncram:altsyncram_component|altsyncram_8982: auto_generated|q_a[7]~_SIM_0PORT_B_READ_ENABLE"——(这是因为fMAX超过芯片最大工作频率,时钟的high/low电平持续时间不够)
Warning: Simultaneous write to memory block address 0 at time 6.89 ns in vector source file -- data is invalid in memory block
三 总结建议
将时序分析相关概念弄清楚后,结合编译报告中Timing Analyzer项,得到tsu、th、tco等时序参数,再调整波形做仿真试验,将理论分析与实践相比照,互相验证。仿真时可以先做功能仿真(前仿真),其特点是不考虑电路门延迟与线延迟,主要验证电路的功能是否符合设计要求。然后进行时序仿真(后仿真),主要验证是否满足时间约束关系、延时、最大工作频率和消耗的资源等。我在做altsyncram读写测试时,所采用的波形与师兄完全相同,以期重复他的结果。但很快发现,师兄并没有做时序分析,而是“1纳秒1纳秒试出来的”,这种具体的“数字试验”与选用器件密切相关。比如我把inclk时钟周期也设为6ns时,输出与师兄的结果有出入,甚至输出从未写入的值。后来才明白,当周期为6ns时,输入数据无法满足tsu要求而出现亚稳态(Violating the setup or hold time on the address registers could corrupt the memory contents),改为8ns后输出相符。可见不同的器件时序结果有所不同,但其时序关系是一致的。基于这个认识,我在做读写测试时采用“参数化分析”(tsu、th、tco等时序参数)的方法,这样即使更换器件,也不影响分析结论。
对于延时不明显的简单电路,可以不考虑时序分析。但当涉及多路寄存器时,一般要进行细致的时序分析,以求设计出来的电路满足时序要求。时序分析时要特别注意三点:其一,必须考虑tsu、th、tco及tpd等参数,不要局限于你所看见的仿真波形,要知道存在大延迟时,时钟沿采到的数据很有可能是之前输入的数据!其二,必须对器件电路或程序对应的电路布局有个整体认识,明确各端口信号的关系,这样可以避免很多不该出现的错误。其三,做到前两点后,做极限测试时建议采用“参数化分析”的方法,因为“1纳秒1纳秒试出来的”的结果往往过于依赖环境变量(如所选器件),调整过程也很麻烦,同时也容易造成实践与理解偏差(前者比如RAM的阵列结构决定了地址线高低位的读取有快慢,从而导致特定地址如5'b10000“试”出的时序结果,对于其他地址如5'b00001却不适用;后者就自不待说了)。
四 附注
1. 大部分外围器件的读写周期在50ns以上。即便是最快的静态RAM,其读写周期也在8ns左右。而ROM的速度一般远远低于RAM,其访问周期一般为100ns~200ns。
采用MOS工艺的存储器,存取周期数为数十至数百ns,而双级型RAM存取周期最快可达10ns以下,一般存储周期略大于存取时间,其差别取决于贮存的物理实现细节。
但对于FPGA内置RAM,读写周期似乎可以达到一两纳秒。
2. Matlab小程序(便于计算)
1 clc,clear all; 2 N = 2; 3 DataParam = [3.523,2.626; 3.510,2.400; 3.429,2.605; 3.383,2.346; 2.640,2.475; 2.825,2.660]; 4 Interval = max(DataParam(:,1)) - min(DataParam(:,2)); 5 ClkPosedge = max(DataParam(:,1)) + [0:N-1] * Interval; 6 for idx = 1:N 7 idx 8 Clk = ClkPosedge(idx) 9 DataElapse = ClkPosedge(idx) - DataParam 10 end