几个基础且常用的数学算法

你总害怕失去，所以你一直在失去。

前言

此文用于记录学习过程中常用到的函数（较高效的算法）。同时，对函数的原理进行描述，对于相关的更为细致的描述，可以参考文中的参考，写的很好，值得多看。

求最大公因子

1.迭代：

# 欧几里得算法求两个数字的最大公约数
# 迭代：
def gcd(a, b):
    while b != 0:
        tem = a % b
        a = b
        b = tem
    return a

2.递归：

# 欧几里得算法求两个数字的最大公约数
# 递归：
def gcd(a, b):
    if b == 0:
        return a
    else:
        return gcd(b, a % b)

---

扩展欧几里的算法（求逆元）

1.迭代：

# 扩展欧几里的算法
def extendedGCD(a, b):
    #a*xi + b*yi = ri
    if b == 0:
        return (1, 0, a)
    #a*x1 + b*y1 = a
    x1 = 1
    y1 = 0
    #a*x2 + b*y2 = b
    x2 = 0
    y2 = 1
    while b != 0:
        q = a // b
        #ri = r(i-2) % r(i-1)
        r = a % b
        a = b
        b = r
        #xi = x(i-2) - q*x(i-1)
        x = x1 - q*x2
        x1 = x2
        x2 = x
        #yi = y(i-2) - q*y(i-1)
        y = y1 - q*y2
        y1 = y2
        y2 = y
    return(x1, y1, a)

个人觉得不太好理解，可以通过下面列表计算来辅助理解：
定理：

公式：

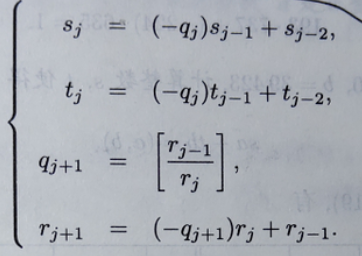
列表记录计算过程：

i	xi	yi	qi	ri
-2	1	0		1859
-1	0	1		1573
0	1	-1	1	286
1	-5	6	5	143
2	-5	6	2	0

解释：
刚开始时，代码中的x1,y1代表表中x-2,y-2; x2,y2代表x-1,y-1 ; a,b分别代表表中r-2,r-1 此例经过三次迭代，b即为0，此时，x1,y1正好对应x1,y1,即-5,6（可以自己算一遍就好理解了，平时手动算时都比较喜欢这种，不容易出错。而且，通过列表计算后，同时也验证了上面的推导因为 a*x + b*y = gcd(a, b)即有，a*xi + b*yi = ri （中间的每一步），从而理解推导过程）

2.递归：
基础：给出任意a, b，必有ax + by = gcd(a, b)。
因为gcd(a, b) = gcd(b, a mod b)，所以一个简单实现是利用gcd算法算出gcd(a, b)再倒回去算 x 和 y 。

# 扩展欧几里的算法
def extendedGCD1(a, b):
    if b == 0:
        return (1, 0, a)
    (x, y, r) = extendedGCD1(b, a%b)
    """
    gcd(a, b) = a*xi + b*yi
    gcd(b, a %  b) = b*xi+1 + (a - [a/b]*b)*yi+1
    gcd(a, b) = gcd(b, a %  b)   =>   a*xi + b*yi = a*yi+1 + b*(xi+1 - [a/b]*yi+1)
    xi = yi+1
    yi = xi+1 - [a/b]*yi+1
    """
    tmp = x
    x = y
    y = tmp - (a//b) * y
    return (x, y, r)

1. 欧几里得算法与扩展欧几里得算法

---

快速幂取模

1.这次又花了点时间看这个算法，之前会但是不够清晰，导致自己写是老出问题。
主要需要明白：

• 积的取余等于取余的积的取余，即

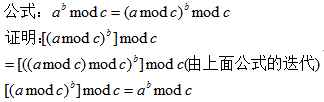
• 分奇偶两种情况，如果是奇数，要多求一步，可以提前算到s中

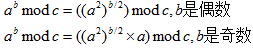
2.迭代实现:

# 快速幂取模算法
# 迭代：
def power(a, b, c):
    s = 1
    a %= c
    while b != 0:
        if b % 2 == 1:
            s = (s * a) % c
        b = b // 2
        a = (a * a) % c
    return s

可参考：

1. 快速幂取模
2. 快速幂取模算法
3. 简单的快速幂算法算法中存在的问题