基于RSA的数字签名方案

坚持坚持，方知何为坚持。

算法分析

1.RSA签名方案是目前使用较多的一个签名方案，它的安全性是基于大整数因式分解的困难性。
2.主要包括算法：

• 秘钥生成算法：
  
• 签名算法：
  
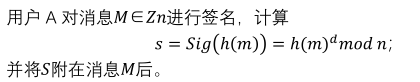
• 验证算法：
  

算法实现

# 直接导入之前写好的RSA算法和hash函数的hashlib库
from RSA import *
import hashlib


# 秘钥生成算法
pubkey = []
selfkey = []
'''公钥私钥中用到的两个大素数数p,q，都是1024位'''
p = 106697219132480173106064317148705638676529121742557567770857687729397446898790451577487723991083173010242416863238099716044775658681981821407922722052778958942891831033512463262741053961681512908218003840408526915629689432111480588966800949428079015682624591636010678691927285321708935076221951173426894836169
q = 144819424465842307806353672547344125290716753535239658417883828941232509622838692761917211806963011168822281666033695157426515864265527046213326145174398018859056439431422867957079149967592078894410082695714160599647180947207504108618794637872261572262805565517756922288320779308895819726074229154002310375209
'''生成公钥私钥'''
pubkey, selfkey = gen_key(p, q)

# 签名算法
m = b"helloworld"
md = hashlib.md5()
md.update(m)
# 用MD5算法生成消息摘要hm
hm = int(md.hexdigest(), 16)
print("Alice生成的消息摘要为： \n", hm)
# 计算签名
# Alice用自己的私钥计算签名s
s = encrypt(hm, selfkey)
print("Alice计算出的签名s为:  \n", s)
# Alice将(m, s)发送个Bob

# 验证算法
# Bob验证签名是否有效
flag = True
# Bob用公钥计算出消息摘要
res = decrypt(s, pubkey)
print("Bob计算出的消息摘要为： \n", res)
if res == hm:
    flag =True
else:
    flag = False
# 将验证结果输出
if flag == True:
    print("Alice的签名有效")
else:
    print("Alice的签名无效")

签名与验证过程

如下图所示，消息m = “helloworld” , 使用RSA算法中生成的公钥和私钥，Alice通过私钥对消息摘要进行签名得到s , Bob通过公钥根据签名s计算出消息摘要，并将其与Alice发来的消息摘要进行对比，如果相等，则打印出签名有效，否则打印出签名无效。

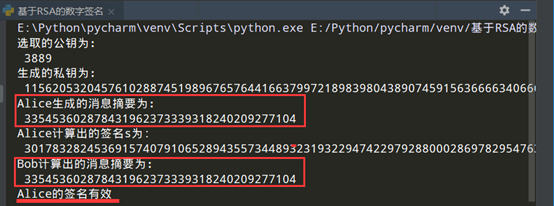
正确性

签名验证过程的正确性证明如下：

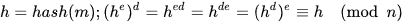
安全性分析

1.签名中使用了hash函数，哈希函数的使用使签名具有更好的抗攻击性。如果不使用，则可根据RSA方案所具有的同态特性，根据已知的两个签名，生成伪造的消息签名。具体如下：如果消息1、2的签名分别是1和2，则任何知道1，1，2，2的人可以伪造对消息12的签名12，因为
(12) = (1)(2)
2.若未使用hash函数，还可以尝试一般攻击：攻击者任选一个数据，用A的公钥计算＝Y^e 于是便可以用Y伪造A对消息X的签名，因为

3.存在签名的可重用性问题，即对同一消息在不同时刻签名是相同的。这个问题可通过在每次签名中引入不同随机数来解决。